Inhaltsverzeichnis
Schritt 1: Bauen Sie einen Stapel auf
Vorwort:
Im vorherigen Blog hatten wir bereits ein vorläufiges Konzept für „Heap“, dann können wir „Heap“ verwenden, um die Probleme in unserem täglichen Leben zu lösen. In diesem Artikel geben wir jeweils zwei häufig verwendete Anwendungsszenarien an. Es ist „Sortieren“. " und "Top-k-Problem". Der vorherige Blog ist in: Simulation Implementation of "Heap"-CSDN Blog
Über „Heap Sort“:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(int* arr, int sz, int parent)
{
int child = parent * 2 + 1;
while (child < sz)
{
if (child + 1 < sz && arr[child] < arr[child + 1])
{
child++;
}
if (arr[child] > arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void AdjustUp(int* arr, int sz, int child)
{
while (child > 0)
{
int parent = (child - 1) / 2;
if (arr[parent] < arr[child])
{
swap(&arr[parent], &arr[child]);
}
child = parent;
}
}
int main()
{
int arr[] = { 2, 6, 9, 3, 1, 7 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sz, i);
}//向下调整算法
//for (int i = 1; i<sz; i++)
//{
// AdjustUp(arr, sz, i);
//}//向上调整算法
int end = sz - 1;
while (end > 0)
{
swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
--end;
}
return 0;
}Schritt 1: Bauen Sie einen Stapel auf
Die Verwendung von „Heap“ kann uns das Sortieren eines bestimmten Arrays außerhalb der Reihenfolge erleichtern. Zuerst sollten wir einen großen Heap für den Sortiervorgang auswählen.
Warum verwenden wir nicht einen kleinen Heap, um einen Heap zu erstellen?
Gemäß der vorherigen Blog-Erklärung zu „Heap“ bedeutet ein kleiner Heap, dass das oberste Element das kleinste Element ist und die Anzahl der anderen Knoten kleiner als das erste Element ist. Wenn es sich also um einen kleinen Heap handelt, ist die kleinste Anzahl bereits vorhanden das erste Element. Wenn Sie das nächstkleinere Element finden möchten, müssen Sie einen Heap unter den verbleibenden Elementen erstellen und den Zyklus wiederholen, um die Sortierung abzuschließen. Dies hat eine hohe Zeitkomplexität und ist für die Sortierung nicht förderlich.
Daher entscheiden wir uns für die Verwendung eines großen Heaps zum Erstellen eines Heaps. Nachdem wir einen großen Heap realisiert haben, tauschen wir das erste und das letzte Element aus und verwenden dann die Abwärtsanpassungsmethode, um die verbleibenden n-1 Elemente anzupassen, und tauschen sie dann aus. Dies kann Sortieren erreichen.
int arr[] = { 2, 6, 9, 3, 1, 7 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = 1; i<sz; i++)
{
AdjustUp(arr, sz, i);
}Passen Sie das Array wie in der Abbildung gezeigt nach oben an, um einen Heap zu erstellen:

Schritt 2: Sortieren
Zuerst tauschen wir das erste und letzte Element:
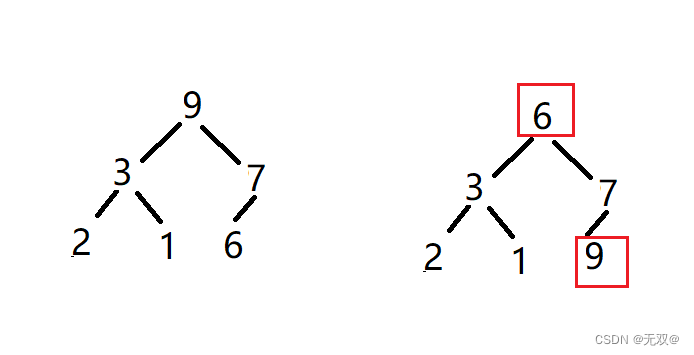
Passen Sie alle Elemente bis auf das letzte Element nach unten an, um einen großen Stapel zu bilden


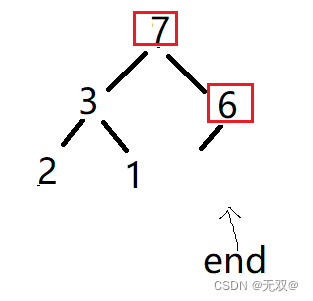
Wiederholen Sie die oben genannten Schritte
Der letzte Haufen ist:

Damit ist die Heap-Sortierung abgeschlossen.
„Top-K-Problem“
Zu den Top-K-Fragen:
Das heißt, die ersten K größten oder kleinsten Elemente in der Datenkombination zu finden. Im Allgemeinen ist die Datenmenge relativ groß .
Zum Beispiel: Top-10-Profis, Fortune 500, Rich List, Top 100 aktive Spieler im Spiel usw. Nehmen wir zur Veranschaulichung das Beispiel der Suche nach den ersten K größten Elementen in n Daten: (unter der Annahme, dass n=10000 ist) (unter der Annahme, dass k=10)
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
const char* file = "data.txt";
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(int* arr, int sz, int parent)
{
int child = 2 * parent + 1;
while (child < sz)
{
if (child + 1 < sz && arr[child + 1] < arr[child])
{
child++;
}
if (arr[child] < arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void CreateFile()
{
//创建随机数的种子
srand((unsigned int)time(NULL));
FILE* Fin = fopen(file, "w");
if (Fin == NULL)
{
perror("Fopen error");
exit(-1);
}
int n = 10000000;
for (int i = 0; i < n; i++)
{
int x = (rand() + i) % n;
fprintf(Fin, "%d\n", x);
}
fclose(Fin);
Fin = NULL;
}
void Print()
{
FILE* Fout = fopen(file, "r");
if (Fout == NULL)
{
perror("Fout error");
exit(-1);
}
//取前k个数进小堆
int* minheap = (int*)malloc(sizeof(int) * 5);
if (minheap == NULL)
{
perror("minheap -> malloc");
return;
}
for (int i = 0; i < 5; i++)
{
fscanf(Fout, "%d", &minheap[i]);
}
for (int i = (5-1-1)/2; i >=0; --i)
{
AdjustDown(minheap, 5, i);
}
//读取数据
int x = 0;
while (fscanf(Fout, "%d", &x) != EOF)
{
if (minheap[0] < x)
{
minheap[0] = x;
}
AdjustDown(minheap, 5, 0);
}
for (int i = 0; i < 5; i++)
{
printf("%d ", minheap[i]);
}
fclose(Fout);
Fout = NULL;
}
int main()
{
//CreateFile();
Print();
return 0;
}Zuerst erstellen wir 10000000 Zufallszahlen, ändern dann die Zahlen, wählen zufällig 5 Zahlen aus und ändern sie als
10000001, 10000002, 10000003, 10000004, 10000005
Bauen Sie einen weiteren kleinen Haufen . Beachten Sie, dass es sich hierbei um einen kleinen Haufen handeln muss!
Wenn wir einen großen Heap erstellen, die Daten zuerst durchsuchen und 10000005 finden, muss sich die Zahl oben im Heap befinden. Wenn wir die nächstkleinere Zahl finden, können wir den Heap nicht betreten, also verwenden wir einen kleinen Heap !
Legen Sie dann die ersten 5 Elemente der Daten in den kleinen Heap.
Durchlaufen und vergleichen Sie dann die verbleibenden 9999995 Zahlen. Wenn sie größer als das oberste Element des Heaps sind, ersetzen Sie sie direkt.
Passen Sie nach dem Ersetzen erneut nach unten an. Nach dem Durchlaufen der gesamten Daten wird der Heap eingefügt.
10000001, 10000002, 10000003, 10000004, 10000005