Teilhaber: Wu Shaojun ｜Schule**: University of Electronic Science and Technology of China**
kurze Einleitung
Die Überwindung des exponentiellen Komplexitätswachstums bei der Simulation von Quanten-Vielteilchensystemen ist ein anspruchsvolles Ziel der Physik. Für die Grundzustandseigenschaften eindimensionaler Quantensysteme stellen derzeit auf Tensornetzwerkzuständen (TNS) basierende Methoden eine effektive Möglichkeit dar, grundsätzlich genaue numerische Lösungen zu liefern. Auch bei zweidimensionalen Systemen wurden einige Fortschritte erzielt, indem einige Algorithmen zur Optimierung von TNS für verschiedene Gittermodelle eingeführt wurden. Dieses Mal werden wir eine neue Quantenzustandsdarstellungsmethode vorstellen, nämlich Isometrisches TNS, das zur Beschreibung des Quantenzustands eines zweidimensionalen Systems verwendet werden kann und rechnerische Vorteile bietet. Darüber hinaus werden wir auch die Verwendung lokaler Messungen vorstellen Rekonstruktion des Quantenzustands. Eine Methode zur Konstruktion von MPS, die nur eine lineare Anzahl von Operationen aufweist.
Verwandte Artikel 1
**Titel: Isometrische Tensornetzwerkzustände in zwei Dimensionen
Autor: Michael P. Zaletel und Frank Pollmann
Zeitschrift: **Phys Rev. Lett.
**Veröffentlichungsdatum:** 24. Januar 2020
Verwandte Artikel 2
**Quelle: Effiziente Quantenzustandstomographie
Quelle: Marcus Cramer, Martin B. Plenio, Steven T. Flammia, Rolando Somma, David Gross, Stephen D. Bartlett, Olivier Landon-Cardinal, David Poulin und Yi-Kai Liu
:** Natur Mitteilungen 1, 149 (2010)
**Veröffentlicht:** 21. Dezember 2010
01
** Einführung
**
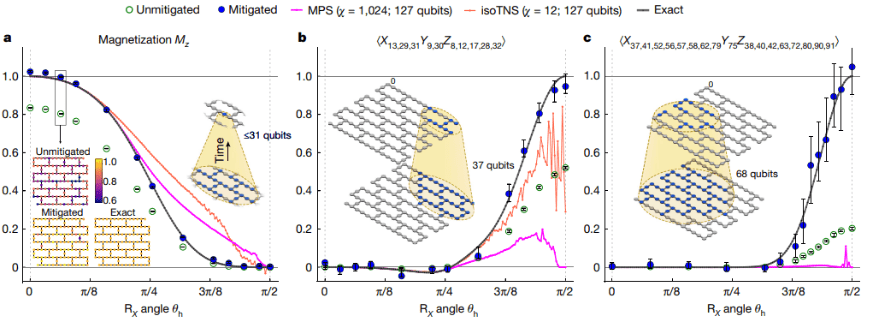
(Bildquelle: Nature Band 618, Seiten 500–505 (2023))
Kürzlich hat IBM die Simulation des zweidimensionalen Transversalfeld-Ising-Modells auf 127 Quantenprozessoren implementiert. Zum Vergleich müssen klassische Simulationen verwendet werden, um genaue Ergebnisse zu erhalten. Diese Arbeit verwendet Gewicht-1-, Gewicht-10- und Gewicht-17-Beobachtungen, um den Quantenschaltkreis des 5-Stufen-Trabers zu messen. Die experimentellen Ergebnisse sind in der Abbildung dargestellt.
Bei der Durchführung klassischer Simulationen zur Erzielung genauer Lösungen wird hier die Light-Cone-and-Depth-Reduced-Methode (LCDR) verwendet. Es ist in zwei Teile unterteilt: Ein Teil besteht darin, die Anzahl der Schaltungsschichten zu reduzieren, die durch die Eigenschaften zwischen Quantengattern simuliert werden müssen. Der andere Teil besteht darin, zu berücksichtigen, dass die mit der Beobachtungsgröße A verbundenen Qubits lokal sind Anstelle aller 127 Bits muss dann nur ein Teil der Qubits berücksichtigt werden. Die zugehörigen Qubit-Zahlen der Beobachtungen mit Gewicht 1, Gewicht 10 und Gewicht 17 betragen 31, 37 bzw. 68. Es ist erwähnenswert, dass die Simulation mit 68 Qubits immer noch über den Möglichkeiten von Brute-Force-Simulationen durch klassische Computer liegt. Daher werden in dieser Arbeit Tensornetzwerke, 1D-Matrixproduktzustände (MPS) und 2D-isometrische Tensornetzwerkzustände (iso TNS) zur Simulation vorgestellt.
02
** Einführung in Matrix Product State (MPS)
**
1. Grundkenntnisse über Tensoren
(1) Definition und grafische Darstellung
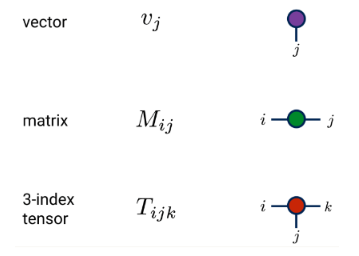
(2) Schrumpfung desselben Indikators
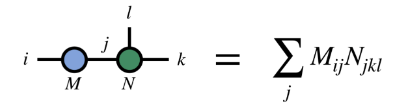
2、MPS
Für ein eindimensionales System mit N Gitterpunkten kann der Mehrkörper-Hilbert-Raum als Tensorprodukt des Gitter-Hilbert-Raums ausgedrückt werden, wenn jeder Gitterpunkt d Quantenzustände hat:
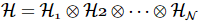
Die entsprechenden willkürlichen Mehrfachhaltungen können ausgedrückt werden als:
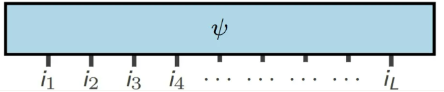
(Bildquelle: arXir:1603.03039, 2016)
Die Kernidee des Matrixproduktzustands (MPS) besteht darin, den Mehrkörperzustand wie folgt auszudrücken:
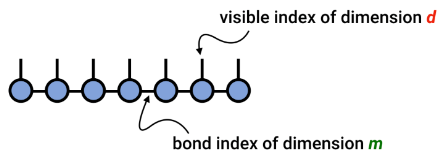
(Bildquelle: arXir:1603.03039, 2016)
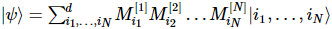
Jede Einheit ist ein Tensor dritter Ordnung, bei dem der physikalische Index der Quantenzustand des Gitterpunkts ist und der Hilfsindex als Quantenverschränkung zwischen ihm und dem linken und rechten System betrachtet werden kann.
SVD-Zerlegung:
Für eine allgemeine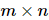 
komplexe Matrix A gibt es eine Zerlegung mit 
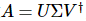, wo
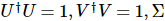ist eine 
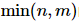Diagonalmatrix mit der Dimension , und die Elemente auf der Diagonale werden Singulärwerte genannt. Im Allgemeinen werden Singularwerte in der Reihenfolge vom größten zum kleinsten entlang der Diagonale angeordnet.
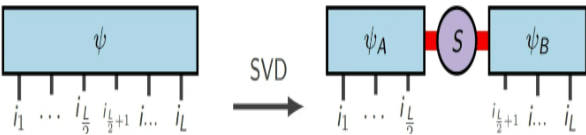
(Bildquelle: arXir:1603.03039, 2016)
Wobei S den singulären Wert darstellt. Wenn die Verschränkung zwischen den beiden Teilen des Systems nicht stark ist, neigt das Spektrum der Singulärwerte dazu, schnell zu zerfallen, und es müssen nur noch weniger Singulärwerte beibehalten werden, um die meisten Informationen der Matrix zu behalten. Angenommen, wir legen fest, dass jede Gruppe von Schmidt-Zerlegungen nicht mehr als m singuläre Werte behält. Am Ende benötigen wir nur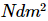 
eine reelle Zahl, um diesen Mehrkörperzustand näherungsweise darzustellen. Im Vergleich zur ursprünglichen Darstellungsmethode, die 
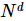einen Parameter erfordert, weist diese Darstellung eine lineare Raumkomplexität für die Anzahl der Gitterpunkte auf, und die Effizienz ist viel höher als die exponentielle Wachstumskomplexität der ursprünglichen Tensorproduktdarstellung.
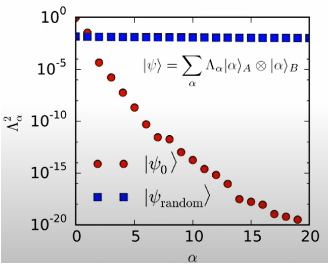
(Bildquelle: arXir:1603.03039, 2016)
Der Prozess zum Erhalten von MPS:
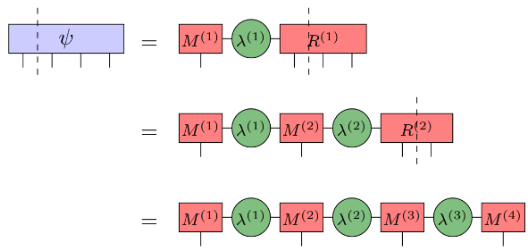
(Bildquelle: arXir:1603.03039, 2016)
WEIL:
Für einen Vielteilchenoperator wie Zustände können wir den Vielteilchenoperator in Matrixproduktform (MPO) schreiben:
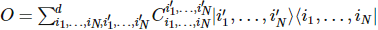
Anders als Zustände kann der aus lokalen Operatoren zusammengesetzte Hamilton-Operator natürlich in Form von Matrixprodukten geschrieben werden:
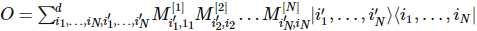
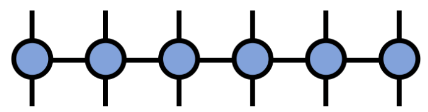
(Bildquelle: arXir:1603.03039, 2016)
Der Matrixproduktoperator behält weiterhin die Matrixproduktstruktur bei, nachdem er auf den Zustand des Matrixprodukts eingewirkt hat:
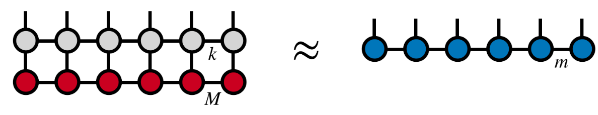
(Bildquelle: arXir:1603.03039, 2016)
03
Isometrische Tensornetzwerkzustände in zwei Dimensionen
1. Zusammenfassung
Tensor-Netzwerkzustände sind ein vielversprechendes, aber numerisch anspruchsvolles Werkzeug für zweidimensionale Quanten-Vielteilchenprobleme. In diesem Artikel stellen die Autoren den isometrisch eingeschränkten TNS-Ansatz vor, eine Form, die eine effiziente Schrumpfung von Tensornetzwerken ermöglicht. Um den Ansatz numerisch zu vergleichen, zeigten die Autoren zunächst, dass die MPS-Darstellung des Grundzustands des zweidimensionalen Transversalfeld-Ising-Modells effektiv in isoTNS umgewandelt werden kann. Tatsächlich implementierten die Autoren einen 2D-TEBD-Algorithmus und zeigten, dass dies effektiv ist findet die isoTNS-Form. Annäherung an den Grundzustand des 2D-Modells.
2. Zustand des isometrischen Tensornetzwerks
1) Isometriebedingung: für eine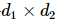 
Dimensionsmatrix M, oder
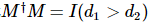. In Tensordiagrammen werden im Allgemeinen Pfeile verwendet, um die Orthogonalität anzuzeigen. Dies bedeutet, dass die Einheitsmatrix durch Verkleinern des nach innen gerichteten Index des Tensors und seines konjugierten Tensors erhalten wird.
2) Kanonische Form von MPS:
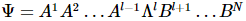
Unter diesen erfüllen A und B die orthogonalen Bedingungen für links und rechts. Die linke orthogonale Bedingung bedeutet, dass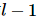 
die Kontraktion des vorherigen Quants und seine eigene Transposition eine Einheitsmatrix sind, und die rechte orthogonale Bedingung bedeutet, dass 
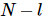die Kontraktion des folgenden Quants und seine eigene Transposition eine Einheitsmatrix ist, 
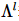die ein diagonales Element darstellt Diagonalmatrix wird auch orthogonales Zentrum genannt.
3) Der erwartete Wert der lokalen Operation kann direkt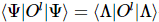 
erhalten werden, da sein externer AB-Tensor gemäß der Isometriebedingung auf 1 schrumpft.
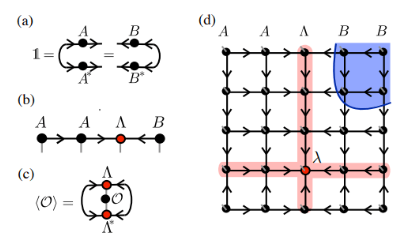
(Bildquelle: Phys. Rev. Lett. 124, 037201)
- Auf zwei Dimensionen verallgemeinern:
In Analogie zur obigen Formel verlangen wir, dass jede Zeile und Spalte von TNS eine Isometrie ist. Diese Einschränkung kann weiter gefordert werden, indem jeder Tensor eine Isometrie sein muss. Wie in Abbildung d oben gezeigt, hat der rote Teil nur nach innen gerichtete Pfeile. Daher handelt es sich um die eindimensionale „orthogonale Hyperfläche“ von TNS,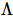 
die die Wellenfunktion unter der Standard-Orthonormalbasis darstellt. Daher 
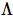kann sie wie MPS verarbeitet werden kann selbst in eine eindimensionale kanonische Form gebracht werden (sein orthogonales Zentrum kann mit dem eindimensionalen kanonischen Algorithmus frei verschoben werden). Für jeden Operator gibt es
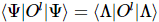eine Dimensionsreduktion des eindimensionalen erwarteten Werts, die vom Standard-MPS-Algorithmus ohne weitere Näherung effizient berechnet werden kann. Dies steht in scharfem Gegensatz zum allgemeinen TNS, bei dem der erwartete Wert die Verwendung einer ungefähren Verkleinerung des gesamten Netzwerks erfordert.
3. Bewegliche orthogonale Hyperfläche
Die zentrale orthogonale Form ist nur dann rechnerisch nützlich, wenn die orthogonale Hyperfläche Lammda effizient durch das Netzwerk bewegt werden kann. In einer Dimension können wir die Bewegung des orthogonalen Zentrums durch die Zerlegung (QR oder SVD) einer beliebigen orthogonalen Matrix erreichen. In zwei Dimensionen müssen wir auch 
die gesamte Spalte verschieben. Für zweidimensionale Systeme ist die Methode der orthogonalen Matrixzerlegung jedoch ungültig, da sie 
die Lokalität zerstört, die für die Darstellung als MPS erforderlich ist.
(Bildquelle: Phys. Rev. Lett. 124, 037201)
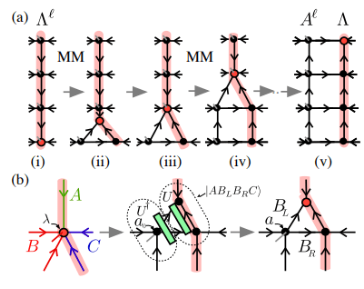
In diesem Artikel verwendet der Autor die Moses Move-Methode, um den Mittelpunkt der orthogonalen Oberfläche zu verschieben. Wie in der obigen Abbildung gezeigt, wird die orthogonale Hyperfläche nach dem MM-Algorithmus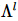 
in das Produkt aus linksorthogonalen 
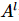Zuständen und Nullspaltenzuständen ohne physikalische Indikatoren unterteilt 
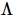. Unter diesen wird die Dekomprimierung durch kontinuierliche Anwendung des in Abbildung (b) gezeigten „Splitting“-Prozesses erreicht. Der Index des Mittelpunkts 
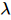wird in drei Zustände gruppiert 
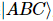und in zwei Schritten in drei Tensoren „aufgespalten“.
4. MPS auf isoNTS erweitert
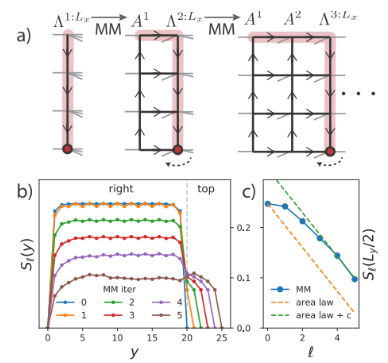
(Bildquelle: Phys. Rev. Lett. 124, 037201)
Angesichts einer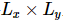 
Grundzustandswellenfunktion schlugen die Autoren einen iterativen Algorithmus vor, der in isoTNS eingesetzt 
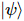werden kann, und testeten das Sing-Transversalfeldmodell. Betrachten Sie einen Streifen und verwenden Sie DMRG, um den Grundzustand eines 1D-MPS zu erhalten, wobei jede „Stelle“ die entsprechende Reihe von Spins enthält [Abbildung (a)]. Wie im dritten Feld in Abbildung a gezeigt, kann MM dann verwendet werden, um die Spalten der Wellenfunktion iterativ zu „aufteilen“ und so isoTNS zu erzeugen. In diesem Beispiel wird die Bindungsdimension als 6 ausgewählt. Wenn g=3,5 (paramagnetische Phase), beträgt der Fehler an jeder Stelle . In diesem Fall, . Die Ergebnisse sind in Abbildung b dargestellt, die zeigt, dass die Verschränkungsentropie der Segmentierung entlang der orthogonalen Hyperfläche mit zunehmender Anzahl der Iterationen abnimmt. Abbildung c zeigt, dass mit zunehmender Anzahl von Iterationen die Verschränkungsentropie linear abnimmt, was den Erwartungen entspricht.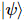
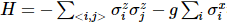
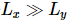
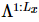
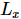
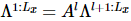
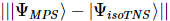
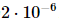
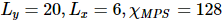
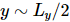
5. 
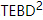Algorithmus
(Bildquelle: Phys. Rev. Lett. 124, 037201)
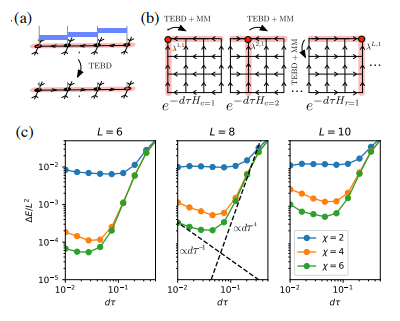
Der Autor hat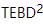 
den Algorithmus auch implementiert. Die Hauptidee von TEBD besteht darin, den auf der Trotter-Suzuki-Zerlegung basierenden Glühalgorithmus zu verwenden, um den zufällig initialisierten MPS-Zustand in den Grundzustand umzuwandeln und den Entwicklungsprozess in ein Tensor-Netzwerk-Schrumpfungsproblem umzuwandeln Verwenden Sie den TEBD-Algorithmus, um die Schrumpfung zu lösen. Insbesondere wird für isoTNS ein Trotterized-Time-Stepper vorgeschlagen, der den Grundzustand durch virtuelle Zeitentwicklung erhalten kann. Unter der Annahme, dass es nur eine Interaktion mit dem nächsten Nachbarn gibt, teilen wir den Hamilton-Operator in Terme auf, die auf Spalten und Zeilen wirken 
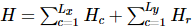, und führen dann Trotterized durch 
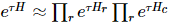, wie in Abbildung (a) gezeigt. Für 1D-TEBD-Updates 
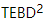kann es problemlos auf zweite Ordnung verbessert werden. Wir 
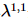beginnen mit dem orthogonalen Zentrum und bewegen das orthogonale Zentrum dann schrittweise, indem wir den Standard-1D-TEBD-Algorithmus und den MM-Algorithmus aufrufen. In einem Scan besteht der Algorithmus tatsächlich aus zwei verschachtelten Versionen von 1D TEBD, daher der Name 
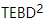. Unter diesen 
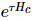wird die Weiterentwicklung von 1D TEBD erreicht, und seine Komplexität ist die 
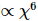von MM , während die vollständige Aktualisierungskomplexität von uneingeschränktem PEPS beträgt
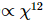. Abbildung (c) zeigt die Energiefehlerdichte des g=3,5-Transversalfeld-Ising-Modells 
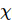als Funktion der Trotter-Schrittgröße für verschiedene Systemgrößen und maximale Bindungsabmessungen 
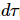. Mit zunehmender Bindungsgröße 
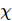nähert sich die minimale Energie dem exakten Ergebnis an.
04
Effiziente Quantenzustandstomographie
1. Zusammenfassung
Die Ableitung von Quantenzuständen aus gemessenen Daten ist für größere Systeme nicht mehr möglich, da die Anzahl der Messungen und der zu ihrer Verarbeitung erforderliche Rechenaufwand exponentiell mit der Systemgröße zunehmen. In diesem Artikel wird ein Tomographieschema vorgeschlagen, das vorteilhafter ist als die direkte Tomographie der Systemgröße. Diese Methode erfordert eine gleichmäßige Manipulation einer konstanten Anzahl von Subsystemen und beruht nur auf einer linearen Anzahl experimenteller Manipulationen. Dieses Schema kann auf eine Vielzahl von Quantenzuständen angewendet werden, insbesondere auf MPS.
2. Schema basierend auf einer einheitlichen Transformation
Die Kernidee dieser Methode besteht darin, eine Folge von Operationen zu finden, um eine Kette von links nach rechts zu entwirren. Jede Operation in dieser Folge ist lokal und unabhängig von der Dimension N.
Nehmen wir an, dass der ideale Zustand ist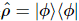 
, und wir gehen davon aus, dass dieser Quantenzustand ein MPS mit einer gegebenen Bindungsdimension von R ist. Ziel dieser Methode ist es, dies zu rekonstruieren 
.
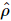Algorithmusprozess:
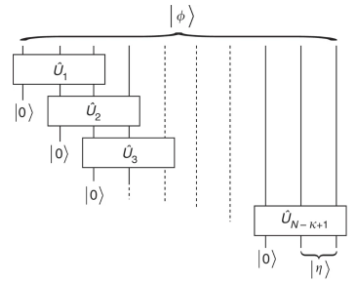
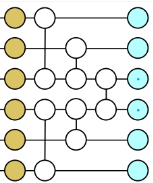
(Bildquelle: Nature Communications 1, 149 (2010))
1) Zuerst nehmen wir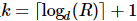 
und führen dann eine Standard-Quantenzustandstomographie an den ersten k Standorten durch. Dann ist die Matrix mit reduzierter Dichte der ersten k Standorte: 
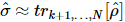Diese Matrix mit reduzierter Dichte weist eine Eigenzerlegung auf 
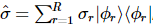, wobei 
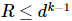. Daher existiert eine Dichtematrix mit einem Qudit weniger, dessen Rang R und Eigenwertsumme gleich 
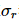sind .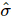
2) Anschließend verwenden wir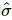 
die Informationen weiter, um eine einheitliche Matrix für die ersten k Positionen zu erstellen 
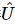, die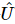 
die erste Stelle entwirren kann.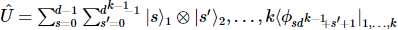
3) Wenden Sie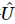 
die Aktion auf den ursprünglichen Zustand an, um Folgendes zu erhalten: 
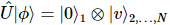Darunter 
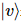gibt es einige 
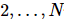reine Zustände in Position.
4). Wiederholen Sie dann den obigen Vorgang für die nächsten 2. bis k+1 Positionen. Analog können wir eine Folge einheitlicher Matrizen erhalten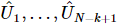 
, von denen jede an Positionen 
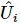wirkt . 
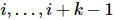Diese Sequenz wird zu 
, 
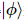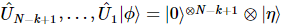wobei jeder 
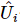in 
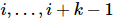Positionen agiert. Diese Sequenz führt dazu 
, 
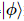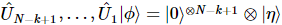dass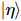 
an den letzten k-1 Positionen einige reine Zustände vorhanden sind.
Zusammenfassend leitet dieses Schema einen Quantenschaltkreis zur Vorbereitung von MPS ab. Die MPS-Zerlegung kann leicht durch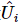 
und erhalten werden.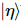
3. Fehler
Der Fehler dieser Methode beruht hauptsächlich auf zwei Aspekten: Zum einen ist es aufgrund der Beschränkung der Bindungsdimension nicht möglich, den Quantenzustand vollständig auszudrücken, und zum anderen liegt der durch die Messung verursachte Fehler vor.
Bei einer geschätzten entwirrten Einheitsmatrix kann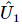 
ein beliebiger Zustand ausgedrückt werden als: , wobei der Fehlervektor ist.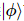
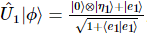
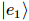
In den nächsten Schritten können wir den Zustand in der folgenden Form erhalten: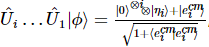 
, wo,
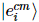ist der kumulative Fehler.
Wir können diesen Fehlervektor abschneiden, indem wir die ersten i Teilchen in der Standardbasis messen und das Ergebnis aller Nullen nachselektieren. Die Wahrscheinlichkeit, dass dies geschieht, beträgt ungefähr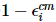 
, und das System bleibt im Zustand 
.
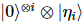Nach einer Reihe einheitlicher Transformationen ist der Endzustand:
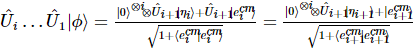
Unter ihnen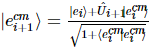 
also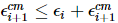 
.
Wir können feststellen, dass sich der Fehler linear mit der Anzahl der Partikel ansammelt und der MPS, den wir erhalten, wie folgt aufgezeichnet wird: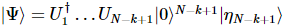 
Dann haben wir: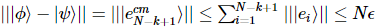
In,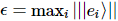 
. Der Gesamtfehler ist höchstens die Summe der Einzelfehler bei jedem Schritt.
Ein in den 1990er Jahren geborener Programmierer hat eine Videoportierungssoftware entwickelt und in weniger als einem Jahr über 7 Millionen verdient. Das Ende war sehr bestrafend! Google bestätigte Entlassungen, die den „35-jährigen Fluch“ chinesischer Programmierer in den Flutter-, Dart- und Teams- Python mit sich brachten stark und wird von GPT-4.5 vermutet; Tongyi Qianwen Open Source 8 Modelle Arc Browser für Windows 1.0 in 3 Monaten offiziell GA Windows 10 Marktanteil erreicht 70 %, Windows 11 GitHub veröffentlicht weiterhin KI-natives Entwicklungstool GitHub Copilot Workspace JAVA ist die einzige starke Abfrage, die OLTP+OLAP verarbeiten kann. Dies ist das beste ORM. Wir treffen uns zu spät.