
▐ URL-Blacklist (Bloom-Filter)
10 Milliarden Blacklist-URLs, jede 64B, wie speichert man diese Blacklist? Stellen Sie fest, ob eine URL in der Blacklist enthalten ist
Hash-tabelle:
Wenn wir die Blacklist als einen Satz betrachten und in einer Hashmap speichern, scheint sie zu groß zu sein und 640 G zu erfordern, was offensichtlich unwissenschaftlich ist.
Bloom-Filter:
Es handelt sich tatsächlich um einen langen binären Vektor und eine Reihe zufälliger Zuordnungsfunktionen.
Es kann verwendet werden, um festzustellen, ob ein Element in einer Menge enthalten ist . Sein Vorteil besteht darin, dass es nur wenig Speicherplatz beansprucht und eine hohe Abfrageeffizienz aufweist. Für einen Bloom-Filter ist sein Wesen ein Bit-Array : Ein Bit-Array bedeutet, dass jedes Element des Arrays nur 1 Bit belegt und jedes Element nur 0 oder 1 sein kann.
Jedes Bit im Array ist ein Binärbit. Der Bloom-Filter verfügt neben einem Bit-Array auch über K-Hash-Funktionen. Wenn dem Bloom-Filter ein Element hinzugefügt wird, werden die folgenden Vorgänge ausgeführt:
Verwenden Sie K-Hash-Funktionen, um K-Berechnungen für den Elementwert durchzuführen und K-Hash-Werte zu erhalten.
Entsprechend dem erhaltenen Hash-Wert wird der entsprechende Indexwert im Bit-Array auf 1 gesetzt.
▐Worthäufigkeitsstatistik (aufgeteilt in Dateien)
2 GB Speicher, um die häufigste Zahl unter 2 Milliarden Ganzzahlen zu finden
Der übliche Ansatz besteht darin, eine Hash-Tabelle zu verwenden, um für jede angezeigte Zahl eine Worthäufigkeitsstatistik zu erstellen. Der Schlüssel der Hash-Tabelle ist eine Ganzzahl, und der Wert zeichnet auf, wie oft die Ganzzahl auftritt. Die Datenmenge in dieser Frage beträgt 2 Milliarden. Um einen Überlauf zu vermeiden, beträgt der Schlüssel der Hash-Tabelle ebenfalls 32 Bit (4B). ). Dann muss ein Datensatz einer Hash-Tabelle 8B belegen.
Wenn die Anzahl der Hash-Tabellendatensätze 200 Millionen beträgt, sind 1,6 Milliarden Bytes erforderlich (8*200 Millionen) und mindestens 1,6 GB Speicher sind erforderlich (1,6 Milliarden/2^30,1 GB==2^30 Bytes== 1000000000). ). Dann erfordern 2 Milliarden Datensätze mindestens 16 GB Speicher, was die Anforderungen der Frage nicht erfüllt.
Die Lösung besteht darin, die große Datei mit 2 Milliarden Zahlen in 16 kleine Dateien aufzuteilen. Gemäß der Hash-Funktion können die 2 Milliarden Daten gleichmäßig auf die 16 Dateien verteilt werden die Hash-Funktion für verschiedene kleine Dateien, vorausgesetzt, die Hash-Funktion ist gut genug. Verwenden Sie dann für jede kleine Datei eine Hash-Funktion, um die Häufigkeit des Vorkommens jeder Zahl zu zählen, sodass wir die Zahl mit den meisten Vorkommen unter den 16 Dateien erhalten, und wählen Sie dann den Schlüssel mit dem höchsten Vorkommen aus den 16 Zahlen aus.
▐Zahl , die nicht erscheint (Bit-Array)
Finden Sie die Zahl, die unter 4 Milliarden nichtnegativen ganzen Zahlen nicht vorkommt
Für das ursprüngliche Problem gilt: Wenn eine Hash-Tabelle zum Speichern der angezeigten Zahlen verwendet wird und im schlimmsten Fall 4 Milliarden Zahlen unterschiedlich sind, muss die Hash-Tabelle 4 Milliarden Daten speichern und eine 32-Bit-Ganzzahl erfordert 4B, dann 4 Milliarden * 4B = 16 Milliarden Bytes Im Allgemeinen erfordern etwa 1 Milliarde Bytes an Daten 1 GB Speicherplatz, sodass etwa 16 GB Speicherplatz erforderlich sind, was die Anforderungen nicht erfüllt.
Ändern wir die Art und Weise und wenden Sie die Array-Größe an: 0 und 1. Wie verwendet man dieses Bit-Array? Haha, die Länge des Arrays entspricht gerade dem Zahlenbereich unserer Ganzzahlen, dann entspricht jeder Indexwert des Arrays einer Zahl in 4294967295 und durchläuft nacheinander 4 Milliarden vorzeichenlose Zahlen. Wenn beispielsweise 20 angetroffen wird, dann bitArray [20] = 1; wenn 666 angetroffen wird, ist bitArray [666] = 1. Ändern Sie nach dem Durchlaufen aller Zahlen die entsprechende Position des Arrays in 1.
Finden Sie eine Zahl, die nicht unter 4 Milliarden nicht-negativen Ganzzahlen vorkommt. Das Speicherlimit beträgt 10 MB.
Für die Verarbeitung einer Milliarde Datenbytes ist etwa 1 GB Speicherplatz erforderlich, sodass 10 MB Speicher 10 Millionen Datenbytes verarbeiten können, was 80 Millionen Bits entspricht. Bei 4 Milliarden nichtnegativen Ganzzahlen sind es 4 Milliarden Bits /080 Millionen Bit = 50, dann kostet die Verarbeitung mindestens 50 Blöcke. Lassen Sie uns mit 64 Blöcken analysieren und antworten.
Fassen Sie die erweiterten Lösungen zusammen
Bestimmen Sie entsprechend der Speichergrenze von 10 MB die Größe des statistischen Intervalls, bei dem es sich um die BitArr-Größe während des zweiten Durchlaufs handelt.
Verwenden Sie die Intervallzählung, um das Intervall mit unzureichenden Zählungen zu finden. In diesem Intervall müssen Zahlen vorhanden sein, die nicht angezeigt werden.
Führen Sie eine Bitmap-Zuordnung der Zahlen in diesem Intervall durch und durchlaufen Sie dann die Bitmap, um eine Zahl zu finden, die nicht angezeigt wird.
Meine eigene Meinung
Wenn Sie nur nach einer Zahl suchen, können Sie High-Bit-Modulus-Operationen ausführen, sie in 64 verschiedene Dateien schreiben und sie dann alles auf einmal über bitArray in der kleinsten Datei verarbeiten.
4 Milliarden vorzeichenlose Ganzzahlen, 1 GB Speicher, alle Zahlen finden, die zweimal vorkommen
Für das ursprüngliche Problem kann eine Bitmap verwendet werden, um das Auftreten von Zahlen darzustellen. Konkret gilt es für ein Bitarrray mit einer Länge von 4294967295×2, um die Wortfrequenz einer Zahl darzustellen. 1B belegt 8 Bits, sodass das Bitarray eine Länge von 4294967295×2 hat belegt 1 GB Speicherplatz. Wie verwende ich dieses BitArr-Array? Durchlaufen Sie diese 4 Milliarden vorzeichenlosen Zahlen. Wenn num zum ersten Mal angetroffen wird, setzen Sie bitArr[num 2+1] und bitArr[num 2] auf 01. Wenn num zum zweiten Mal angetroffen wird, setzen Sie bitArr[num 2+1]. und bitArr[num 2] werden auf 10 gesetzt. Wenn num zum dritten Mal angetroffen wird, werden bitArr[num 2+1] und bitArr[num 2] auf 11 gesetzt. Wenn ich in Zukunft wieder auf num stoße, stelle ich fest, dass bitArr[num 2+1] und bitArr[num 2] zu diesem Zeitpunkt auf 11 gesetzt sind, sodass keine weiteren Einstellungen vorgenommen werden. Nachdem der Durchlauf abgeschlossen ist, durchlaufen Sie bitArr nacheinander. Wenn festgestellt wird, dass bitArr[i 2+1] und bitArr[i 2] auf 10 gesetzt sind, ist i die Zahl, die zweimal erscheint.
▐Doppelte URL (maschinell)
Finden Sie doppelte URLs unter 10 Milliarden URLs
Die Lösung des ursprünglichen Problems verwendet eine herkömmliche Methode zur Lösung von Big-Data-Problemen: Zuweisen großer Dateien zu Maschinen über eine Hash-Funktion oder Aufteilen großer Dateien in kleine Dateien über eine Hash-Funktion. Diese Division wird durchgeführt, bis das Ergebnis der Division die Ressourcenbeschränkungen erfüllt. Zunächst müssen Sie den Interviewer nach den Ressourcenbeschränkungen fragen, einschließlich der Anforderungen an Speicher, Rechenzeit usw. Nach Klärung der Restriktionsanforderungen kann jede URL über eine Hash-Funktion mehreren Maschinen zugeordnet oder in mehrere kleine Dateien aufgeteilt werden. Die genaue Anzahl „mehrerer“ wird hierbei anhand spezifischer Ressourcenbeschränkungen berechnet.
Beispielsweise wird eine große Datei mit 10 Milliarden Bytes über eine Hash-Funktion an 100 Maschinen verteilt, und dann zählt jede Maschine, ob in den ihr zugewiesenen URLs doppelte URLs vorhanden sind. Gleichzeitig bestimmt die Art der Hash-Funktion, ob Die gleiche URL ist Es ist unmöglich, die URL auf verschiedene Computer zu verteilen oder die große Datei über die Hash-Funktion auf einem einzelnen Computer aufzuteilen und dann die Hash-Tabellendurchquerung für jede kleine Datei zu verwenden, um doppelte URLs zu finden Verteilen Sie es an die Maschine. Oder sortieren Sie die Dateien nach dem Aufteilen und prüfen Sie nach dem Sortieren, ob doppelte URLs vorhanden sind. Kurz gesagt: Bedenken Sie, dass viele große Datenprobleme untrennbar mit dem Auslagern verbunden sind. Entweder verteilt die Hash-Funktion den Inhalt der großen Datei auf verschiedene Computer, oder die Hash-Funktion teilt die große Datei in kleine Dateien auf und verarbeitet dann jede kleine Anzahl .
▐ TOPK-Suche (kleiner Wurzelhaufen)
Durchsuchen Sie eine große Anzahl von Wörtern und finden Sie die beliebtesten TOP100-Wörter.
Zu Beginn nutzten wir die Idee des Hash-Shunts, um Vokabeldateien mit Dutzenden Milliarden Daten auf verschiedene Maschinen zu übertragen. Die spezifische Anzahl der Maschinen wurde vom Interviewer oder weiteren Einschränkungen bestimmt. Wenn für jede Maschine die Menge der verteilten Daten immer noch groß ist, beispielsweise aufgrund von unzureichendem Speicher oder anderen Problemen, kann die Hash-Funktion verwendet werden, um die verteilten Dateien jeder Maschine zur Verarbeitung in kleinere Dateien aufzuteilen.
Bei der Verarbeitung jeder kleinen Datei zählt die Hash-Tabelle jedes Wort und seine Worthäufigkeit. Nachdem der Hash-Tabellendatensatz erstellt wurde, wird beim Durchlaufen der Hash-Tabelle ein kleiner Root-Heap der Größe 100 verwendet Top100 jeder kleinen Datei (die gesamten unsortierten Top100). Jede kleine Datei verfügt über einen eigenen kleinen Root-Heap mit Worthäufigkeit (die gesamten unsortierten Top100). Durch Sortieren der Wörter im kleinen Root-Heap nach Worthäufigkeit erhält man die sortierten Top100 jeder kleinen Datei. Sortieren Sie dann die Top 100 jeder kleinen Datei extern oder verwenden Sie weiterhin den kleinen Root-Heap, um die Top 100 auf jedem Computer auszuwählen. Die Top 100 zwischen verschiedenen Maschinen werden dann extern sortiert oder verwenden weiterhin den kleinen Root-Heap, und schließlich werden die Top 100 der gesamten Daten in zweistelliger Milliardenhöhe erhalten. Für das Top-K-Problem werden neben der Hash-Funktionsumleitung und der Worthäufigkeitsstatistik mithilfe von Hash-Tabellen häufig auch Heap-Strukturen und externe Sortierung verwendet, um damit umzugehen.
▐Median (einseitige binäre Suche)
10 MB Speicher, ermitteln Sie den Median von 10 Milliarden ganzen Zahlen
Genügend Speicher: Wenn Sie über genügend Speicher verfügen, warum sollten Sie sich dann Sorgen machen? Sortieren Sie einfach alle 10 Milliarden Elemente ... und finden Sie dann einfach das eine in der Mitte. Aber glauben Sie, dass der Interviewer Ihnen Erinnerung schenken wird? ?
Unzureichender Speicher: Die Frage besagt, dass es sich um eine Ganzzahl handelt, aber wir glauben, dass es sich um eine Ganzzahl mit Vorzeichen handelt, also 4 Bytes groß ist und 32 Bits belegt.
Nehmen Sie an, dass 10 Milliarden Zahlen in einer großen Datei gespeichert sind, lesen Sie einen Teil der Datei nacheinander in den Speicher (wobei die Speichergrenze nicht überschritten wird), stellen Sie jede Zahl binär dar und vergleichen Sie das höchste Bit der Binärdatei (Bit 32, Vorzeichenbit, 0 ist positiv, 1 ist negativ. Wenn das höchste Bit der Zahl 0 ist, wird die Zahl in die Datei file_0 geschrieben. Wenn das höchste Bit 1 ist, wird die Zahl in die Datei file_1 geschrieben.
Somit werden 10 Milliarden Zahlen in zwei Dateien aufgeteilt. Nehmen wir an, dass die Datei file_0 6 Milliarden Zahlen und die Datei file_1 4 Milliarden Zahlen enthält. Dann befindet sich der Median in der Datei file_0 und ist die milliardste Zahl nach Sortierung aller Zahlen in der Datei file_0. (Die Zahlen in Datei_1 sind alle negative Zahlen und die Zahlen in Datei_0 sind alle positive Zahlen. Das heißt, es gibt insgesamt nur 4 Milliarden negative Zahlen, daher muss sich die 5-milliardste Zahl nach der Sortierung in Datei_0 befinden.)
Jetzt müssen wir nur noch die Datei file_0 verarbeiten (die Datei file_1 muss nicht mehr berücksichtigt werden). Ergreifen Sie für die Datei „file_0“ die gleichen Maßnahmen wie oben: Lesen Sie einen Teil der Datei „file_0“ der Reihe nach in den Speicher (wobei das Speicherlimit nicht überschritten wird), stellen Sie jede Zahl binär dar, vergleichen Sie das zweithöchste Bit der Binärdatei (das 31. Bit), Wenn das zweithöchste Bit der Zahl 0 ist, schreiben Sie es in die Datei file_0_0. Wenn das zweithöchste Bit 1 ist, schreiben Sie es in die Datei file_0_1.
Unter der Annahme, dass es 3 Milliarden Zahlen in Datei_0_0 und 3 Milliarden Zahlen in Datei_0_1 gibt, beträgt der Median: die milliardste Zahl, nachdem die Zahlen in Datei_0_0 von klein nach groß sortiert wurden.
Verlassen Sie die Datei file_0_1 und teilen Sie die Datei file_0_0 weiterhin entsprechend der nächsthöheren Ziffer (der 30. Stelle) auf. Nehmen Sie an, dass die beiden geteilten Dateien dieses Mal sind: Es gibt 500 Millionen Zahlen in Datei_0_0_0 und 2,5 Milliarden Zahlen in Datei_0_0_1 ist die 500-millionste Zahl nach dem Sortieren aller Zahlen in der Datei file_0_0_1.
Gemäß der obigen Idee können die Zahlen schnell und direkt sortiert werden, um den Median zu ermitteln, bis die geteilte Datei direkt in den Speicher geladen werden kann.
▐Short Domain Name System (Caching)
Entwerfen Sie ein kurzes Domainnamensystem, um lange URLs in kurze URLs umzuwandeln.
Bei Verwendung des Nummernzuweisers ist der Anfangswert 0. Für jede Anfrage zur Generierung einer Kurzverbindung wird der Wert des Nummernzuweisers erhöht und dieser Wert dann in 62 Hexadezimalzahlen (a-zA-Z0-9) umgewandelt, wie zum Beispiel der erste Anfrage Zum Zeitpunkt der Anfrage ist der Wert des Nummernzuweisers 0, entsprechend hexadezimal a. Bei der zweiten Anfrage ist der Wert des Nummernzuweisers 1, entsprechend hexadezimal b Der Nummernzuweiser ist 10000, entsprechend Die hexadezimale Schreibweise ist sBc.
Verketten Sie den Domänennamen des Kurzlink-Servers mit dem 62-Hexadezimalwert des Zuweisers als Zeichenfolge, bei der es sich um die URL des Kurzlinks handelt, zum Beispiel: t.cn/sBc.
Umleitungsprozess: Nach dem Generieren eines Kurzlinks müssen Sie die Zuordnungsbeziehung zwischen dem Kurzlink und dem Langlink speichern, d. h. sBc -> URL. Wenn der Browser auf den Kurzlinkserver zugreift, erhält er den ursprünglichen Link URL-Pfad und führt dann eine 302-Umleitung durch. Zuordnungsbeziehungen können mit KV wie Redis oder Memcache gespeichert werden.
▐Massiver Kommentarspeicher (Nachrichtenwarteschlange)
Angenommen, es gibt ein solches Szenario. Die Anzahl der Kommentare zu den Nachrichten kann groß sein.
Die Frontend-Seite wird dem Benutzer direkt angezeigt und asynchron über die Nachrichtenwarteschlange in der Datenbank gespeichert.
▐Anzahl der Online-/gleichzeitigen Benutzer (Redis)
-
Lösungsideen zur Anzeige der Anzahl der Online-Benutzer auf einer Website
-
Online-Benutzertabelle pflegen -
Verwendung von Redis-Statistiken
-
Zeigt die Anzahl der gleichzeitigen Benutzer der Website an
-
Immer wenn ein Benutzer auf den Dienst zugreift, wird die Benutzer-ID in die ZSORT-Warteschlange geschrieben und die Gewichtung entspricht der aktuellen Zeit. -
Berechnen Sie die Anzahl der Benutzer der Organisation Zrange innerhalb einer Minute anhand des Gewichts (d. h. der Zeit); -
Löschen Sie Zrem-Benutzer, die seit mehr als einer Minute abgelaufen sind.
▐Beliebte Zeichenfolgen (Präfixbaum)
HashMap-Methode
Obwohl die Gesamtzahl der Zeichenfolgen relativ groß ist, überschreitet sie nach der Deduplizierung nicht 300 W. Daher können Sie erwägen, alle Zeichenfolgen und ihre Auftrittszeiten in einer HashMap zu speichern 4 Stellt die 4 Bytes dar, die von der Ganzzahl belegt werden. Man erkennt, dass 1G Speicherplatz völlig ausreicht.
Die Idee ist wie folgt
Durchlaufen Sie zunächst die Zeichenfolge, speichern Sie sie direkt in der Karte. Wenn sie in der Karte enthalten ist, wird 1 zum entsprechenden Wert hinzugefügt O(N).
Durchlaufen Sie dann die Karte, um einen kleinen oberen Heap mit 10 Elementen zu erstellen. Wenn die Anzahl der Vorkommen der durchlaufenen Zeichenfolge größer ist als die Anzahl der Vorkommen der Zeichenfolge am oberen Rand des Heaps, ersetzen Sie sie und passen Sie den Heap an eine kleine Obergrenze an Haufen.
Nach Abschluss des Durchlaufs sind die 10 Zeichenfolgen im Heap die Zeichenfolgen, die am häufigsten angezeigt werden. Die zeitliche Komplexität dieses Schritts O(Nlog10).
Präfixbaummethode
Wenn diese Zeichenfolgen viele gleiche Präfixe haben, können Sie die Verwendung eines Präfixbaums in Betracht ziehen, um die Anzahl der Vorkommen der Zeichenfolge zu zählen. Die Knoten des Baums speichern die Anzahl der Vorkommen der Zeichenfolge, und 0 bedeutet kein Vorkommen.
Die Idee ist wie folgt
Suchen Sie beim Durchlaufen der Zeichenfolge im Präfixbaum. Fügen Sie 1 zur Anzahl der im Knoten gespeicherten Zeichenfolgen hinzu. Fügen Sie nach Abschluss der Konstruktion das Vorkommen der Zeichenfolge hinzu Blattknoten. Die Häufigkeit ist auf 1 festgelegt.
Schließlich wird der kleine obere Heap noch verwendet , um die Anzahl der Vorkommen der Zeichenfolge zu sortieren.
▐Red- Envelope-Algorithmus
Lineare Schneidmethode, bei der N-1 Messer in einem Intervall geschnitten werden. Je früher desto besser
Doppelte Mittelwertmethode, zufällig in [0~verbleibende Menge/verbleibende Anzahl von Personen*2], relativ einheitlich

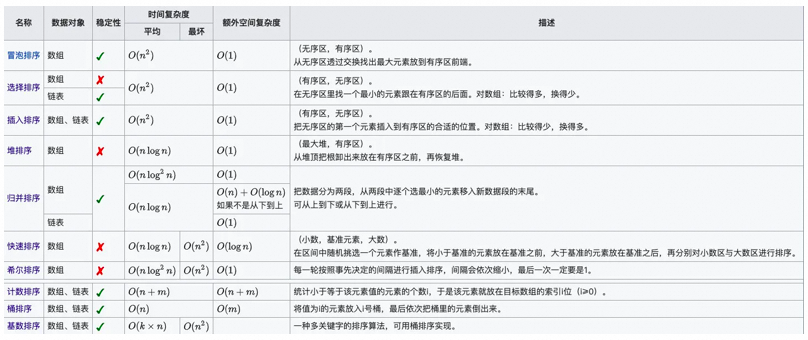
▐Schnelle Sortierung der Handschrift
public class QuickSort {public static void swap(int[] arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}/* 常规快排 */public static void quickSort1(int[] arr, int L , int R) {if (L > R) return;int M = partition(arr, L, R);quickSort1(arr, L, M - 1);quickSort1(arr, M + 1, R);}public static int partition(int[] arr, int L, int R) {if (L > R) return -1;if (L == R) return L;int lessEqual = L - 1;int index = L;while (index < R) {if (arr[index] <= arr[R])swap(arr, index, ++lessEqual);index++;}swap(arr, ++lessEqual, R);return lessEqual;}/* 荷兰国旗 */public static void quickSort2(int[] arr, int L, int R) {if (L > R) return;int[] equalArea = netherlandsFlag(arr, L, R);quickSort2(arr, L, equalArea[0] - 1);quickSort2(arr, equalArea[1] + 1, R);}public static int[] netherlandsFlag(int[] arr, int L, int R) {if (L > R) return new int[] { -1, -1 };if (L == R) return new int[] { L, R };int less = L - 1;int more = R;int index = L;while (index < more) {if (arr[index] == arr[R]) {index++;} else if (arr[index] < arr[R]) {swap(arr, index++, ++less);} else {swap(arr, index, --more);}}swap(arr, more, R);return new int[] { less + 1, more };}// for testpublic static void main(String[] args) {int testTime = 1;int maxSize = 10000000;int maxValue = 100000;boolean succeed = true;long T1=0,T2=0;for (int i = 0; i < testTime; i++) {int[] arr1 = generateRandomArray(maxSize, maxValue);int[] arr2 = copyArray(arr1);int[] arr3 = copyArray(arr1);// int[] arr1 = {9,8,7,6,5,4,3,2,1};long t1 = System.currentTimeMillis();quickSort1(arr1,0,arr1.length-1);long t2 = System.currentTimeMillis();quickSort2(arr2,0,arr2.length-1);long t3 = System.currentTimeMillis();T1 += (t2-t1);T2 += (t3-t2);if (!isEqual(arr1, arr2) || !isEqual(arr2, arr3)) {succeed = false;break;}}System.out.println(T1+" "+T2);// System.out.println(succeed ? "Nice!" : "Oops!");}private static int[] generateRandomArray(int maxSize, int maxValue) {int[] arr = new int[(int) ((maxSize + 1) * Math.random())];for (int i = 0; i < arr.length; i++) {arr[i] = (int) ((maxValue + 1) * Math.random())- (int) (maxValue * Math.random());}return arr;}private static int[] copyArray(int[] arr) {if (arr == null) return null;int[] res = new int[arr.length];for (int i = 0; i < arr.length; i++) {res[i] = arr[i];}return res;}private static boolean isEqual(int[] arr1, int[] arr2) {if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null))return false;if (arr1 == null && arr2 == null)return true;if (arr1.length != arr2.length)return false;for (int i = 0; i < arr1.length; i++)if (arr1[i] != arr2[i])return false;return true;}private static void printArray(int[] arr) {if (arr == null)return;for (int i = 0; i < arr.length; i++)System.out.print(arr[i] + " ");System.out.println();}}
▐Handschriftverschmelzung
public static void merge(int[] arr, int L, int M, int R) {int[] help = new int[R - L + 1];int i = 0;int p1 = L;int p2 = M + 1;while (p1 <= M && p2 <= R)help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];while (p1 <= M)help[i++] = arr[p1++];while (p2 <= R)help[i++] = arr[p2++];for (i = 0; i < help.length; i++)arr[L + i] = help[i];}public static void mergeSort(int[] arr, int L, int R) {if (L == R)return;int mid = L + ((R - L) >> 1);process(arr, L, mid);process(arr, mid + 1, R);merge(arr, L, mid, R);}public static void main(String[] args) {int[] arr1 = {9,8,7,6,5,4,3,2,1};mergeSort(arr, 0, arr.length - 1);printArray(arr);}
▐Handgeschriebene Stapel
// 堆排序额外空间复杂度O(1)public static void heapSort(int[] arr) {if (arr == null || arr.length < 2)return;for (int i = arr.length - 1; i >= 0; i--)heapify(arr, i, arr.length);int heapSize = arr.length;swap(arr, 0, --heapSize);// O(N*logN)while (heapSize > 0) { // O(N)heapify(arr, 0, heapSize); // O(logN)swap(arr, 0, --heapSize); // O(1)}}// arr[index]刚来的数,往上public static void heapInsert(int[] arr, int index) {while (arr[index] > arr[(index - 1) / 2]) {swap(arr, index, (index - 1) / 2);index = (index - 1) / 2;}}// arr[index]位置的数,能否往下移动public static void heapify(int[] arr, int index, int heapSize) {int left = index * 2 + 1; // 左孩子的下标while (left < heapSize) { // 下方还有孩子的时候// 两个孩子中,谁的值大,把下标给largest// 1)只有左孩子,left -> largest// 2) 同时有左孩子和右孩子,右孩子的值<= 左孩子的值,left -> largest// 3) 同时有左孩子和右孩子并且右孩子的值> 左孩子的值, right -> largestint largest = left+1 < heapSize && arr[left+1]> arr[left] ? left+1 : left;// 父和较大的孩子之间,谁的值大,把下标给largestlargest = arr[largest] > arr[index] ? largest : index;if (largest == index)break;swap(arr, largest, index);index = largest;left = index * 2 + 1;}}public static void swap(int[] arr, int i, int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}public static void main(String[] args) {int[] arr1 = {9,8,7,6,5,4,3,2,1};heapSort(arr1);printArray(arr1);}
▐Handgeschriebener Singleton
public class Singleton {private volatile static Singleton singleton;private Singleton() {}public static Singleton getSingleton() {if (singleton == null) {synchronized (Singleton.class) {if (singleton == null) {singleton = new Singleton();}}}return singleton;}}
▐Handgeschriebener LRUcache
// 基于linkedHashMappublic class LRUCache {private LinkedHashMap<Integer,Integer> cache;private int capacity; //容量大小public LRUCache(int capacity) {cache = new LinkedHashMap<>(capacity);this.capacity = capacity;}public int get(int key) {//缓存中不存在此key,直接返回if(!cache.containsKey(key)) {return -1;}int res = cache.get(key);cache.remove(key); //先从链表中删除cache.put(key,res); //再把该节点放到链表末尾处return res;}public void put(int key,int value) {if(cache.containsKey(key)) {cache.remove(key); //已经存在,在当前链表移除}if(capacity == cache.size()) {//cache已满,删除链表头位置Set<Integer> keySet = cache.keySet();Iterator<Integer> iterator = keySet.iterator();cache.remove(iterator.next());}cache.put(key,value); //插入到链表末尾}}
//手写双向链表class LRUCache {class DNode {DNode prev;DNode next;int val;int key;}Map<Integer, DNode> map = new HashMap<>();DNode head, tail;int cap;public LRUCache(int capacity) {head = new DNode();tail = new DNode();head.next = tail;tail.prev = head;cap = capacity;}public int get(int key) {if (map.containsKey(key)) {DNode node = map.get(key);removeNode(node);addToHead(node);return node.val;} else {return -1;}}public void put(int key, int value) {if (map.containsKey(key)) {DNode node = map.get(key);node.val = value;removeNode(node);addToHead(node);} else {DNode newNode = new DNode();newNode.val = value;newNode.key = key;addToHead(newNode);map.put(key, newNode);if (map.size() > cap) {map.remove(tail.prev.key);removeNode(tail.prev);}}}public void removeNode(DNode node) {DNode prevNode = node.prev;DNode nextNode = node.next;prevNode.next = nextNode;nextNode.prev = prevNode;}public void addToHead(DNode node) {DNode firstNode = head.next;head.next = node;node.prev = head;node.next = firstNode;firstNode.prev = node;}}
▐Handschrift- Thread-Pool
package com.concurrent.pool;import java.util.HashSet;import java.util.Set;import java.util.concurrent.ArrayBlockingQueue;import java.util.concurrent.BlockingQueue;public class MySelfThreadPool {//默认线程池中的线程的数量private static final int WORK_NUM = 5;//默认处理任务的数量private static final int TASK_NUM = 100;private int workNum;//线程数量private int taskNum;//任务数量private final Set<WorkThread> workThreads;//保存线程的集合private final BlockingQueue<Runnable> taskQueue;//阻塞有序队列存放任务public MySelfThreadPool() {this(WORK_NUM, TASK_NUM);}public MySelfThreadPool(int workNum, int taskNum) {if (workNum <= 0) workNum = WORK_NUM;if (taskNum <= 0) taskNum = TASK_NUM;taskQueue = new ArrayBlockingQueue<>(taskNum);this.workNum = workNum;this.taskNum = taskNum;workThreads = new HashSet<>();//启动一定数量的线程数,从队列中获取任务处理for (int i=0;i<workNum;i++) {WorkThread workThread = new WorkThread("thead_"+i);workThread.start();workThreads.add(workThread);}}public void execute(Runnable task) {try {taskQueue.put(task);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}}public void destroy() {System.out.println("ready close thread pool...");if (workThreads == null || workThreads.isEmpty()) return ;for (WorkThread workThread : workThreads) {workThread.stopWork();workThread = null;//help gc}workThreads.clear();}private class WorkThread extends Thread{public WorkThread(String name) {super();setName(name);}@Overridepublic void run() {while (!interrupted()) {try {Runnable runnable = taskQueue.take();//获取任务if (runnable !=null) {System.out.println(getName()+" readyexecute:"+runnable.toString());runnable.run();//执行任务}runnable = null;//help gc} catch (Exception e) {interrupt();e.printStackTrace();}}}public void stopWork() {interrupt();}}}package com.concurrent.pool;public class TestMySelfThreadPool {private static final int TASK_NUM = 50;//任务的个数public static void main(String[] args) {MySelfThreadPool myPool = new MySelfThreadPool(3,50);for (int i=0;i<TASK_NUM;i++) {myPool.execute(new MyTask("task_"+i));}}static class MyTask implements Runnable{private String name;public MyTask(String name) {this.name = name;}public String getName() {return name;}public void setName(String name) {this.name = name;}@Overridepublic void run() {try {Thread.sleep(1000);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}System.out.println("task :"+name+" end...");}@Overridepublic String toString() {// TODO Auto-generated method stubreturn "name = "+name;}}}
▐Handschriftliches Verbraucherproduzentenmuster
public class Storage {private static int MAX_VALUE = 100;private List<Object> list = new ArrayList<>();public void produce(int num) {synchronized (list) {while (list.size() + num > MAX_VALUE) {System.out.println("暂时不能执行生产任务");try {list.wait();} catch (InterruptedException e) {e.printStackTrace();}}for (int i = 0; i < num; i++) {list.add(new Object());}System.out.println("已生产产品数"+num+" 仓库容量"+list.size());list.notifyAll();}}public void consume(int num) {synchronized (list) {while (list.size() < num) {System.out.println("暂时不能执行消费任务");try {list.wait();} catch (InterruptedException e) {e.printStackTrace();}}for (int i = 0; i < num; i++) {list.remove(0);}System.out.println("已消费产品数"+num+" 仓库容量" + list.size());list.notifyAll();}}}public class Producer extends Thread {private int num;private Storage storage;public Producer(Storage storage) {this.storage = storage;}public void setNum(int num) {this.num = num;}public void run() {storage.produce(this.num);}}public class Customer extends Thread {private int num;private Storage storage;public Customer(Storage storage) {this.storage = storage;}public void setNum(int num) {this.num = num;}public void run() {storage.consume(this.num);}}public class Test {public static void main(String[] args) {Storage storage = new Storage();Producer p1 = new Producer(storage);Producer p2 = new Producer(storage);Producer p3 = new Producer(storage);Producer p4 = new Producer(storage);Customer c1 = new Customer(storage);Customer c2 = new Customer(storage);Customer c3 = new Customer(storage);p1.setNum(10);p2.setNum(20);p3.setNum(80);c1.setNum(50);c2.setNum(20);c3.setNum(20);c1.start();c2.start();c3.start();p1.start();p2.start();p3.start();}}
▐Handschriftblockierungswarteschlange
public class blockQueue {private List<Integer> container = new ArrayList<>();private volatile int size;private volatile int capacity;private Lock lock = new ReentrantLock();private final Condition isNull = lock.newCondition();private final Condition isFull = lock.newCondition();blockQueue(int capacity) {this.capacity = capacity;}public void add(int data) {try {lock.lock();try {while (size >= capacity) {System.out.println("阻塞队列满了");isFull.await();}} catch (Exception e) {isFull.signal();e.printStackTrace();}++size;container.add(data);isNull.signal();} finally {lock.unlock();}}public int take() {try {lock.lock();try {while (size == 0) {System.out.println("阻塞队列空了");isNull.await();}} catch (Exception e) {isNull.signal();e.printStackTrace();}--size;int res = container.get(0);container.remove(0);isFull.signal();return res;} finally {lock.unlock();}}}public static void main(String[] args) {AxinBlockQueue queue = new AxinBlockQueue(5);Thread t1 = new Thread(() -> {for (int i = 0; i < 100; i++) {queue.add(i);System.out.println("塞入" + i);try {Thread.sleep(500);} catch (InterruptedException e) {e.printStackTrace();}}});Thread t2 = new Thread(() -> {for (; ; ) {System.out.println("消费"+queue.take());try {Thread.sleep(800);} catch (InterruptedException e) {e.printStackTrace();}}});t1.start();t2.start();}
▐Handschriftliches Multithread-Alternativdruck-ABC
package com.demo.test;import java.util.concurrent.locks.Condition;import java.util.concurrent.locks.ReentrantLock;public class syncPrinter implements Runnable{// 打印次数private static final int PRINT_COUNT = 10;private final ReentrantLock reentrantLock;private final Condition thisCondtion;private final Condition nextCondtion;private final char printChar;public syncPrinter(ReentrantLock reentrantLock, Condition thisCondtion, Condition nextCondition, char printChar) {this.reentrantLock = reentrantLock;this.nextCondtion = nextCondition;this.thisCondtion = thisCondtion;this.printChar = printChar;}@Overridepublic void run() {// 获取打印锁 进入临界区reentrantLock.lock();try {// 连续打印PRINT_COUNT次for (int i = 0; i < PRINT_COUNT; i++) {//打印字符System.out.print(printChar);// 使用nextCondition唤醒下一个线程// 因为只有一个线程在等待,所以signal或者signalAll都可以nextCondtion.signal();// 不是最后一次则通过thisCondtion等待被唤醒// 必须要加判断,不然虽然能够打印10次,但10次后就会直接死锁if (i < PRINT_COUNT - 1) {try {// 本线程让出锁并等待唤醒thisCondtion.await();} catch (InterruptedException e) {e.printStackTrace();}}}} finally {reentrantLock.unlock();}}public static void main(String[] args) throws InterruptedException {ReentrantLock lock = new ReentrantLock();Condition conditionA = lock.newCondition();Condition conditionB = lock.newCondition();Condition conditionC = lock.newCondition();Thread printA = new Thread(new syncPrinter(lock, conditionA, conditionB,'A'));Thread printB = new Thread(new syncPrinter(lock, conditionB, conditionC,'B'));Thread printC = new Thread(new syncPrinter(lock, conditionC, conditionA,'C'));printA.start();Thread.sleep(100);printB.start();Thread.sleep(100);printC.start();}}
▐Alternativ FooBar drucken
//手太阴肺经 BLOCKING Queuepublic class FooBar {private int n;private BlockingQueue<Integer> bar = new LinkedBlockingQueue<>(1);private BlockingQueue<Integer> foo = new LinkedBlockingQueue<>(1);public FooBar(int n) {this.n = n;}public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; i++) {foo.put(i);printFoo.run();bar.put(i);}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n; i++) {bar.take();printBar.run();foo.take();}}}//手阳明大肠经CyclicBarrier 控制先后class FooBar6 {private int n;public FooBar6(int n) {this.n = n;}CyclicBarrier cb = new CyclicBarrier(2);volatile boolean fin = true;public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; i++) {while(!fin);printFoo.run();fin = false;try {cb.await();} catch (BrokenBarrierException e) {}}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n; i++) {try {cb.await();} catch (BrokenBarrierException e) {}printBar.run();fin = true;}}}//手少阴心经 自旋 + 让出CPUclass FooBar5 {private int n;public FooBar5(int n) {this.n = n;}volatile boolean permitFoo = true;public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; ) {if(permitFoo) {printFoo.run();i++;permitFoo = false;}else{Thread.yield();}}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n; ) {if(!permitFoo) {printBar.run();i++;permitFoo = true;}else{Thread.yield();}}}}//手少阳三焦经 可重入锁 + Conditionclass FooBar4 {private int n;public FooBar4(int n) {this.n = n;}Lock lock = new ReentrantLock(true);private final Condition foo = lock.newCondition();volatile boolean flag = true;public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; i++) {lock.lock();try {while(!flag) {foo.await();}printFoo.run();flag = false;foo.signal();}finally {lock.unlock();}}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n;i++) {lock.lock();try {while(flag) {foo.await();}printBar.run();flag = true;foo.signal();}finally {lock.unlock();}}}}//手厥阴心包经 synchronized + 标志位 + 唤醒class FooBar3 {private int n;// 标志位,控制执行顺序,true执行printFoo,false执行printBarprivate volatile boolean type = true;private final Object foo= new Object(); // 锁标志public FooBar3(int n) {this.n = n;}public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; i++) {synchronized (foo) {while(!type){foo.wait();}printFoo.run();type = false;foo.notifyAll();}}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n; i++) {synchronized (foo) {while(type){foo.wait();}printBar.run();type = true;foo.notifyAll();}}}}//手太阳小肠经 信号量 适合控制顺序class FooBar2 {private int n;private Semaphore foo = new Semaphore(1);private Semaphore bar = new Semaphore(0);public FooBar2(int n) {this.n = n;}public void foo(Runnable printFoo) throws InterruptedException {for (int i = 0; i < n; i++) {foo.acquire();printFoo.run();bar.release();}}public void bar(Runnable printBar) throws InterruptedException {for (int i = 0; i < n; i++) {bar.acquire();printBar.run();foo.release();}}}
本文分享自微信公众号 - 大淘宝技术(AlibabaMTT)。
如有侵权,请联系 [email protected] 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。
