[Path planning] Matlab source code for path planning based on A star and improved A star

The A* algorithm is a heuristic search algorithm, which is improved based on the Dijkstra algorithm.

Problem introduction

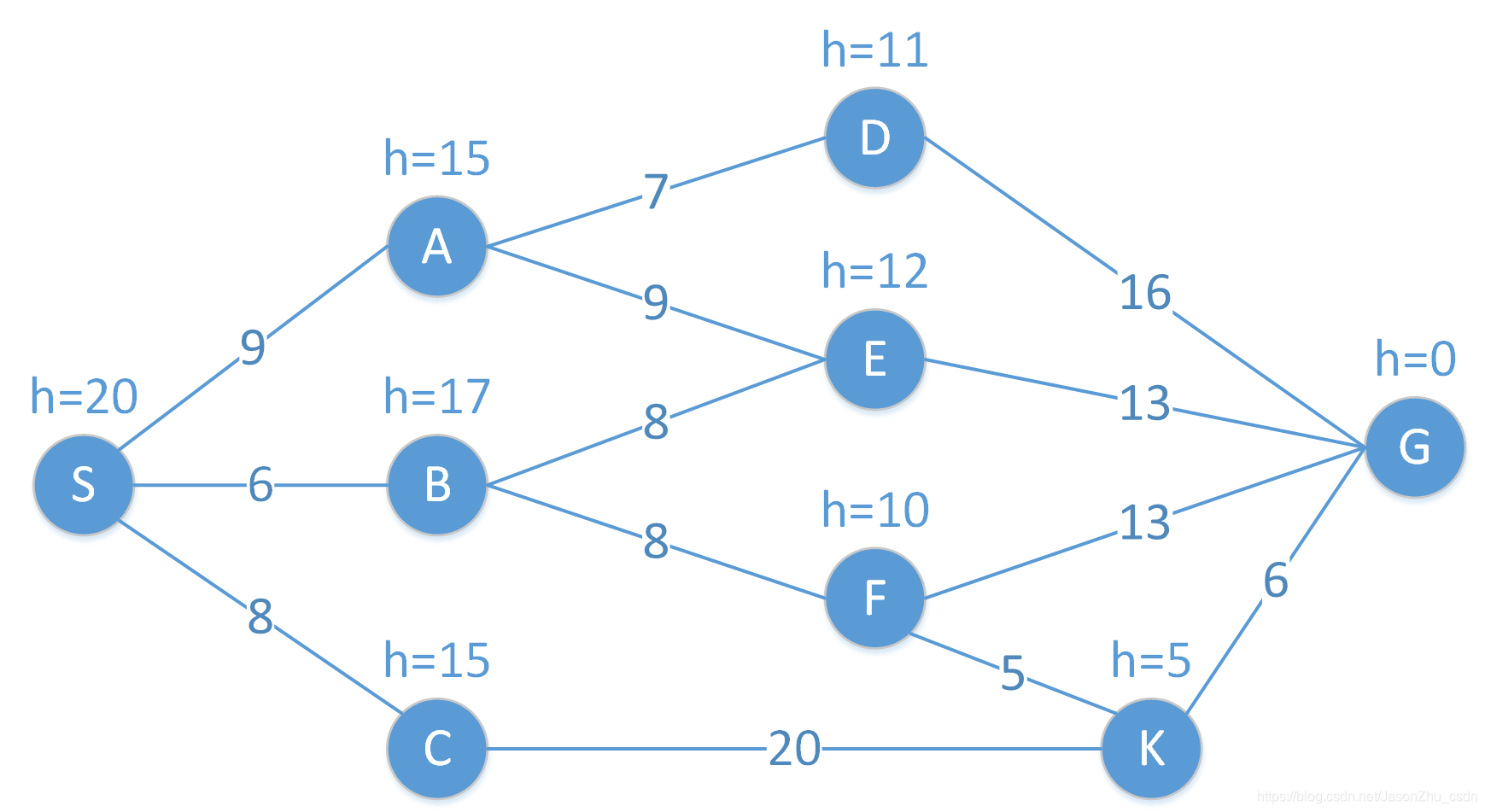
As shown in the figure below, S is the start node and G is the goal node.

The connection between nodes is the path length between two points, such as the path length from A to E c(A,E) = 9.
The h value next to the node is the estimated value of the current node reaching the target node (G), such as h(A)=15, which means that the estimated path length from the current point A to the target point G is 15, where h(x) is For the heuristic function, there are many methods for designing the heuristic function. For details, please refer to the link, which is not expanded here.
The length of the path from the starting point S to the current node x is denoted as g(x).
The estimated distance length from the starting point S to the target G through the point x is expressed as f(x) = g(x) + h(x) , which is the core formula of the A* algorithm.
The A* algorithm gradually builds the shortest path by continuously selecting the node with the smallest estimated distance f.

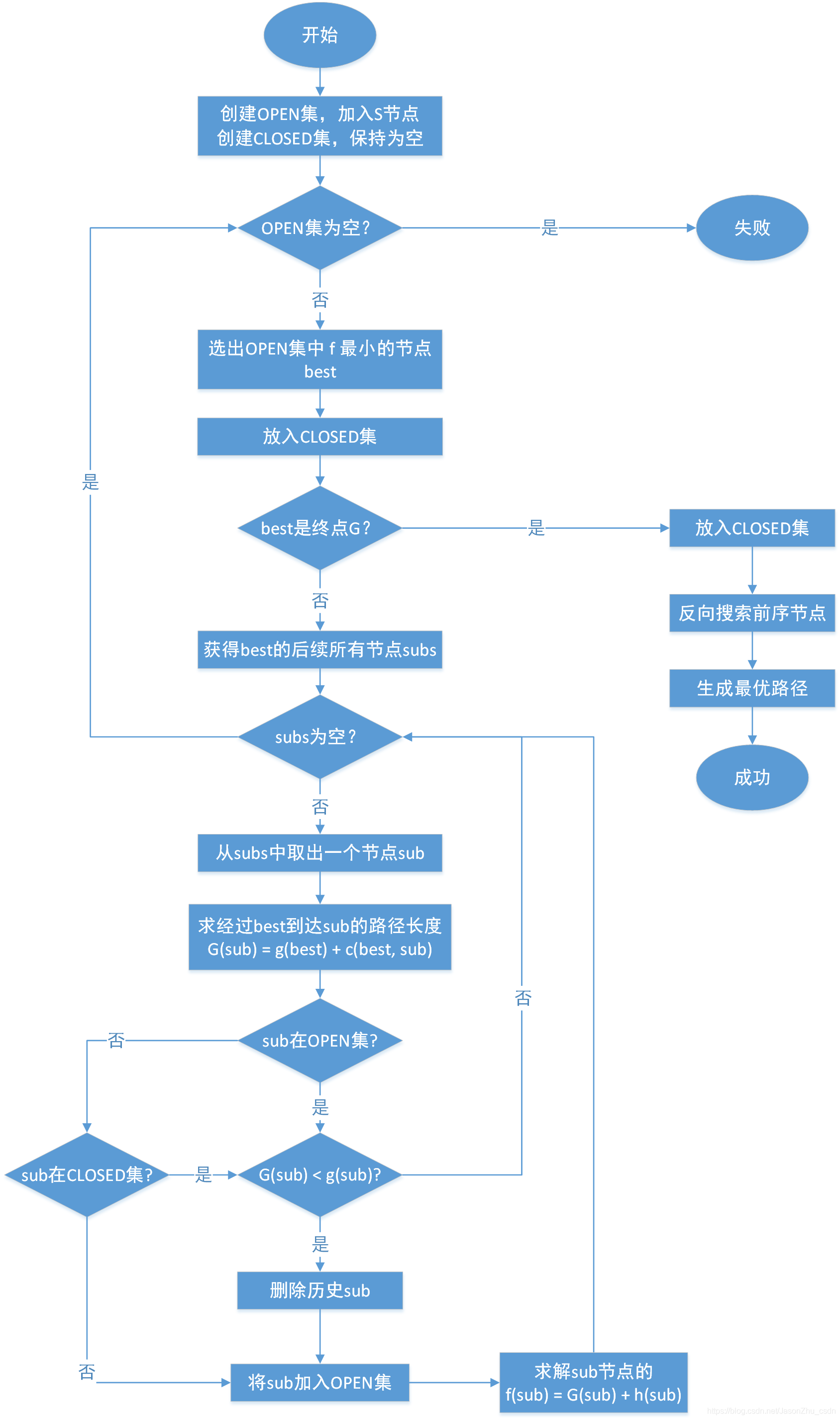
Logic flow

Create two sets OPEN set and CLOSED set. The core of the algorithm is to select the optimal node from the OPEN set (the smaller f value is the best, or if f is the same, the smaller h is better) to the CLOSED set, and then put its successor nodes into OPEN is concentrated, and then the operation is repeated to select the optimal node until the target is reached, or the OPEN is empty. Finally, CLOSED concentrates on searching for the starting point S in reverse order based on the pre-order nodes contained in the target G. The reverse order of this link is the optimal path. The specific flow is as shown in the figure below.

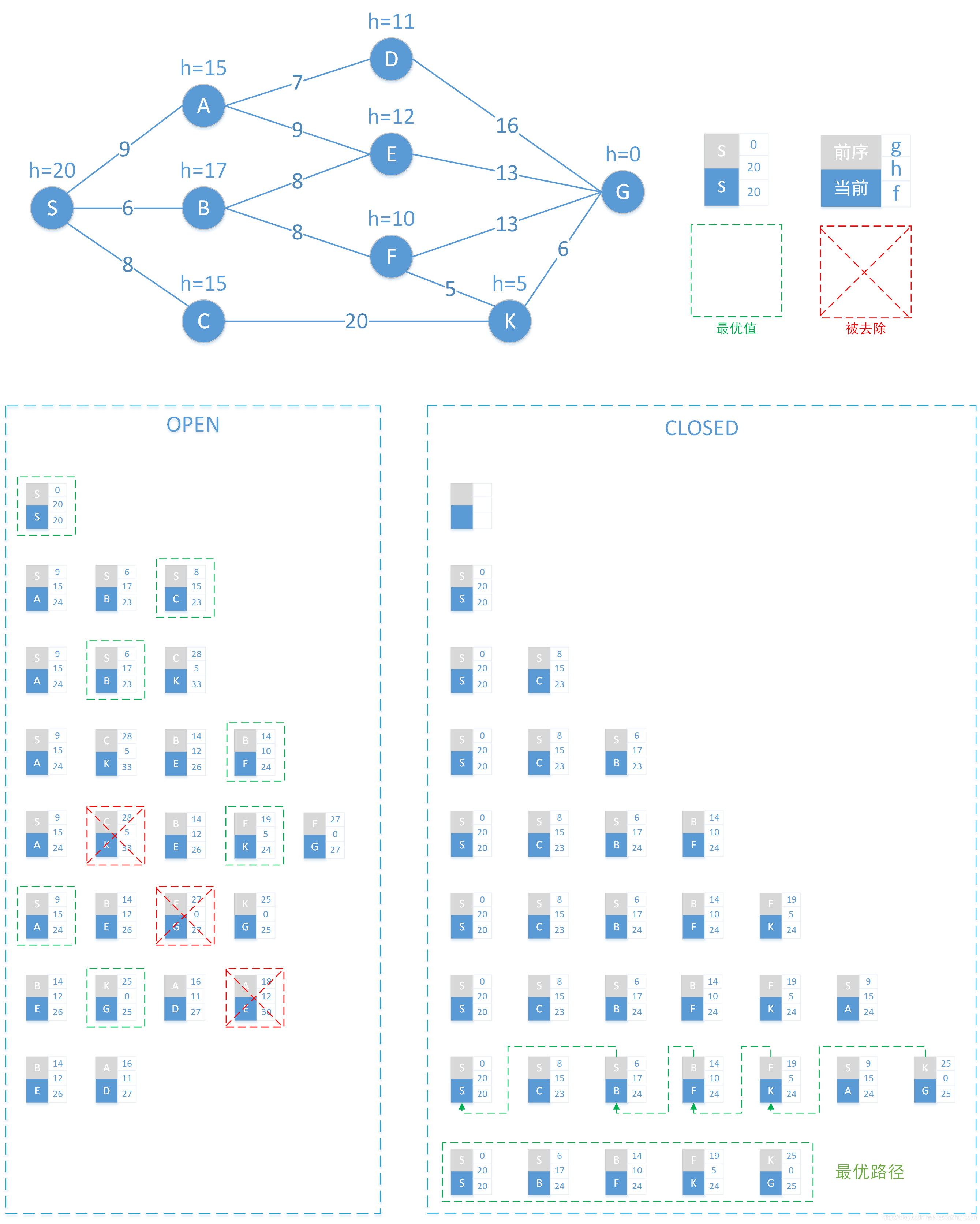
Search process

The following is an expanded view of the search process of the previous network.

In the combination block:

Gray is the preorder node
Blue current node x
g: the path distance from the starting point S to the current node x.
h: the estimated distance from the current node x to the end point G
f: the estimated distance from the starting point S to the end point G, that is, f = g + h
The green box is the optimal node in the current OPEN set
The red box indicates the node that needs to be deleted in the current OPEN set

Each row in OPEN and CLOSED represents the set of nodes in the two sets when a complete iteration is completed.

The final optimal path is: S->B->F->k->G

Note: When the two nodes f are the same, the smaller h is better

%**************************************************************************



disp('  Generating Grid ... ');
co=or;
crn=s;

noOfNodes  = nooc*noor;
nodmat=ones(nooc,noor,3);
nodmat(1:noOfNodes)=1:noOfNodes;
nodmat(:,:,2)=(find(nodmat(:,2,2)==1))*ones(1,noor);
nodmat(:,:,3)=ones(nooc,1)*(find(nodmat(2,:,3)==1));
nodmat(:,:,1)=flipdim((nodmat(:,:,1)),2);
nodmat(:,:,2)=flipdim((nodmat(:,:,2)),2);
nodmat(:,:,3)=flipdim((nodmat(:,:,3)),2);
noddata=reshape(nodmat,noOfNodes,3);


%rand('state', 0);

if plot_flag==1
    scrsz = get(0,'ScreenSize');
    h=figure(gcf);
    set(h,'Position',[scrsz(3)/8 scrsz(4)/8 scrsz(3)-2*scrsz(3)/8 ...
        scrsz(4)-2*scrsz(4)/8]);
    clf;
    hold on;
end


Astar_coor=noddata(:,2:3)*GTS;


netXloc = Astar_coor(:,1)';
netYloc = Astar_coor(:,2)';
axis([min(netXloc)-20  max(netXloc)+30  min(netYloc)-20  max(netYloc)+30])
Astar_connect = zeros(noOfNodes, noOfNodes);
Astar_coord = zeros(noOfNodes, 2);
for i = 1:noOfNodes
    
    Astar_coord(i,1) = netXloc(i);
    Astar_coord(i,2) = netYloc(i);
    
    for j = 1:noOfNodes
        distance = sqrt((netXloc(i) - netXloc(j))^2 + (netYloc(i) - netYloc(j))^2);
        ll=isempty(find(o==i, 1));
        lm=isempty(find(o==j, 1));
        if (distance <= R && ll==1 && lm==1)
            matrix(i, j) = distance;   % if set to '1', Dijkstra computes Spath in terms of hops; if set to 'distance', it is the real shortest path
            if i~=j % must be satisfied
                Astar_connect(i, j) = 1;
            else
                Astar_connect(i, j) = 0;
            end
            if plot_flag==1
                line([netXloc(i) netXloc(j)], [netYloc(i) netYloc(j)], 'color',[.65 .65 .65],'LineStyle', ':');
            end
        else
            matrix(i, j) = inf;
            Astar_connect(i, j) = 0;
        end;
    end;
end
for i = 1:noOfNodes
    if plot_nodenum
        text(netXloc(i)+20, netYloc(i), num2str(i));
    end
    if plot_flag==1
        
        if i==s
            plot(netXloc(i), netYloc(i),'square','MarkerSize',12,'MarkerFaceColor','g');
            hold on;
            
        end
        if i==d
            plot(netXloc(i), netYloc(i),'square','MarkerSize',12,'MarkerFaceColor','r');
        end
        
        if isempty(find(o==i))
            plot(netXloc(i), netYloc(i),'.');
        end
        
        
    end
end;


% activeNodes = [];
% for i = 1:noOfNodes,
%     % initialize the farthest node to be itself;
%     farthestPreviousHop(i) = i;     % used to compute the RTS/CTS range;
%     farthestNextHop(i) = i;
% end;

Astar_coord=Astar_coord';
%Astar_connect;
%%
disp('Generating Paths ... ')
%[path, totalCost, farthestPreviousHop, farthestNextHop] = dijkstra(noOfNodes, matrix, s, d, farthestPreviousHop, farthestNextHop);
% combo = [noOfNodes s-1 d-1 R/2];
%[Astar_path, Astar_search] = Astar(Astar_coord', Astar_connect, combo); % notice, we must put Astar_coord' rather than Astar_coord
%[Astar_paths,cost_astar,astar_time] = Astarm(Astar_coord, Astar_connect, s , d);
%[Astar_path,Astar_search]=Astar(Astar_coord, Astar_connect, combo);
[Astar_path,cost_astar,astar_time,Astar_dist] =komegaA(Astar_coord, Astar_connect, s, d, 1, inf, 0);
[komega_path,cost_komega,ko_time,komega_dist]=komegaA(Astar_coord, Astar_connect, s, d, k , b, n);
%%
if disp_summary==1
    Astar_path, komega_path,cost_astar,cost_komega,astar_time,ko_time, Astar_dist, komega_dist
end

if ~isempty(Astar_path)
    for i = 1:(length(Astar_path)-1)
        if plot_flag==1
            astr=line([netXloc(Astar_path(i)) netXloc(Astar_path(i+1))], [netYloc(Astar_path(i)) netYloc(Astar_path(i+1))], 'Color','r','LineWidth', 2, 'LineStyle', '-.');
            if plot_nodenum==1
                text(netXloc(i), netYloc(i), num2str(i));
            end
        end
    end;
end;
if ~isempty(komega_path)
    for i = 1:(length(komega_path)-1)
        if plot_flag==1
            kom=line([netXloc(komega_path(i)) netXloc(komega_path(i+1))], [netYloc(komega_path(i)) netYloc(komega_path(i+1))], 'Color','g','LineWidth', 2, 'LineStyle', '-');
            if plot_nodenum==1
                text(netXloc(i), netYloc(i), num2str(i));
            end
        end
    end;
end;

rest=title('Comparison Between A-Star and K-Omega');
set(rest,'Interpreter','latex');
dkstr=strcat('K-Omega(k=',num2str(k),' b=',num2str(b),' n=',num2str(n),')');
kleg=legend([astr kom],'A-Star',dkstr);hold on;
set(kleg,'Interpreter','latex');



if plot_flag == 1
    hold off;
end

% Execute if K-Omega has not yet executed harware
if (n==0)
    [done]=execnxt(komega_path);
end

% If Analysis mode requested, perform analysis
if AnalysisMode==1
    AnalyzeKO;
end

Complete code or write on behalf of adding QQ1575304183