Palindrome of linked list
Title description
For a linked list, please design an algorithm with a time complexity of O(n) and an additional space complexity of O(1) to determine whether it is a palindrome structure.
Given the head pointer A of a linked list, please return a bool value indicating whether it is a palindrome. Ensure that the length of the linked list is less than or equal to 900.
Example 1
1->2->2->1
Example 2
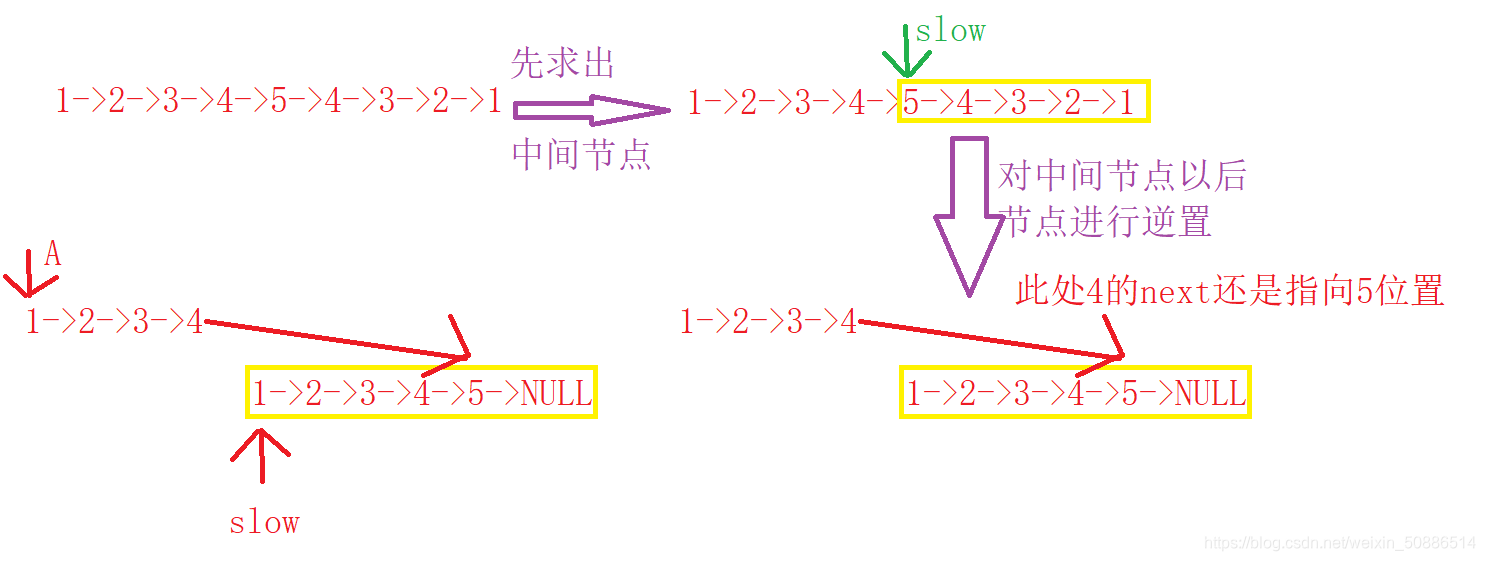
1->2->3->4->5->4->3->2->1
Language: C language
Idea analysis
The palindrome structure is actually a linked list that is symmetric about the middle. We can use the fast and slow pointer method to find the middle number. If it is an even number of nodes, it is the second number in the middle. At this time, the node pointed to by the slow pointer is the middle node. The node is inverted to the end of the linked list, and then the inverted node and the head node are compared one by one, until one side is empty.
The diagram is as follows:
Code
class PalindromeList
{
public:
bool chkPalindrome(ListNode* A)
{
//求中间节点
ListNode* fast = A;
ListNode* slow = A;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
//逆置
ListNode* tem = slow;//保存slow位置,给p
slow = NULL;//制空slow,因为最后一个节点要指向
ListNode* p = tem;
ListNode* p1 = p->next;
while(p)
{
p->next = slow;
slow = p;
p = p1;
//防止p1=NULL还求next
if(p1)
{
p1 = p1->next;
}
}
//判断前后是否相等
while(A && slow)
{
if(A->val == slow->val)
{
A = A->next;
slow = slow->next;
}
else
{
return false;
}
}
return true;
}
};