[Optimization solution] Urban traffic signal optimization based on matalb improved genetic algorithm (GA+IGA) [including Matlab source code 213]

1. Introduction

1 The basic theory of genetic algorithm
Genetics believes that inheritance is an instruction genetic code encapsulated in each cell and contained in the chromosome in the form of genes. Each gene has a special position and controls a special property. The individual produced by each gene has a certain degree of adaptability to the environment. Gene hybridization and mutation may produce offspring that are adaptable to the environment. Through natural selection of the survival of the fittest, the gene structure with high fitness value is preserved.
The genetic algorithm draws on the genetic theory of "survival of the fittest" and expresses the solution of the optimization problem as the "survival of the fittest" process of "chromosomes". Through the evolution of generations of duplication, crossover, and mutation of the "chromosome" group, we finally get It is the individual who is most adaptable to the environment to get the optimal or satisfactory solution to the problem. This is a highly parallel, random and adaptive general optimization algorithm.
A series of advantages of genetic algorithm have made it more and more important in recent years, and it has been widely used in solving optimization problems in many fields, including its successful application in the transportation field.
2 Characteristics of
genetic algorithm Genetic algorithm is a self-adaptive global optimization probabilistic search algorithm formed by simulating the genetic and evolutionary process in biological natural environment. It is a kind of robust search algorithm that can be used in the optimization calculation of complex systems. Compared with other optimization algorithms, it has many characteristics.
There are three main traditional optimization algorithms: enumeration, heuristic and search algorithms:
1. Enumeration method
Enumeration method enumerates all feasible solutions in the feasible solution set to find the exact optimal solution. For continuous functions, this method requires discretization first, so that the optimal solution may never be reached due to the discrete processing. In addition, when the enumeration space is relatively large, the solution efficiency of this algorithm is very low and extremely time-consuming.
2. Heuristic algorithm The
heuristic algorithm seeks a heuristic rule that can produce a feasible solution to find an optimal solution or approximate optimal solution. The efficiency of the heuristic algorithm is relatively high, but for each problem that needs to be solved, its unique heuristic rule must be found. This heuristic rule is generally not universal and not suitable for other problems.
3. Search algorithm
The search algorithm performs a search operation in a subset of the feasible solution set to find the optimal solution or approximate optimal solution of the problem. Although the search algorithm cannot guarantee that the optimal solution of the problem will be obtained, if some heuristic knowledge is appropriately used, a better balance can be achieved between the quality and efficiency of the approximate solution.
3 The workflow of the basic genetic algorithm
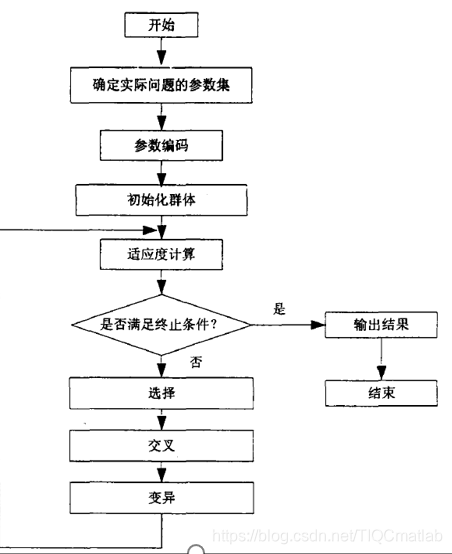
Insert picture description here
4 Fitness function

5 Selection operator
Selection, also known as replication, is the process of selecting individuals with strong vitality in a group to generate a new group. The genetic algorithm uses selection operators to perform survival of the fittest on individuals in the group, and selects according to the fitness of each individual. Individuals with higher fitness are more likely to be inherited into the next-generation population; vice versa. In this way, the fitness value of the individuals in the group can be continuously approached to the optimal solution. The determination of the selection operator directly affects the calculation results of the genetic algorithm.
Here are some typical and commonly used selection operators:
1. Roulette selection
2. Random competition selection
3. Random traversal selection
4. Sort selection
5. League selection
6 Crossover operator
The following introduces several crossover operators suitable for binary coded individuals or decimal coded individuals.
l. Single-point crossover
single-point crossover (One-point Crossover), also known as a simple cross, and is the most common basic cross operators. It starts with a random selection point in a binary string. For each pair of individuals that are paired with each other, they exchange partial chromosomes of the two individuals at their crossover points according to the set crossover probability, thereby generating two new individuals.
2.
Two-point crossover and multi-point crossover Two-point crossover refers to the setting of two crossover points in the individual code string and then partial gene exchange. The specific process of two-point crossing is:
(1) Two crossing points are set immediately in the two individual code strings that are paired with each other.
(2) Exchange part of the chromosomes of two individuals between the two set intersection points.
3. Uniform crossover
Uniform crossover means that the genes at each locus of two paired individuals are exchanged with the same crossover probability to form two new individuals. The specific operation can be used to determine how each gene of the new individual is provided by which parent individual by setting a mask.
4. Arithmetic crossover
Arithmetic crossover refers to the linear combination of two individuals to produce two new individuals. In order to be able to perform linear combination operations, the operation object of arithmetic intersection is generally the individual represented by the floating-point number code.
7 Mutation operator The
so-called mutation operation in the genetic algorithm refers to replacing the gene value of some locus in the individual chromosome coding string with other alleles of the locus to form a new individual. Mutation is one of the main methods of genetic algorithm to generate new individuals. Mutation operation can make the algorithm maintain the diversity of the population during operation, effectively avoid premature maturity, and improve the local search ability of genetic algorithm.
The mutation operator in genetic algorithm should also be selected and designed according to different requirements. The following are several commonly used mutation operators.
8 Improvement of genetic algorithm
Insert picture description here

Second, the source code

%% GA
%% 清空环境变量
clc,clear,close all
warning off
% feature jit off
%% 遗传算法参数初始化
maxgen = 50;                      % 进化代数，即迭代次数
sizepop = 100;                     % 种群规模
pcross = [0.7];                    % 交叉概率选择，0和1之间
pmutation = [0.1];                 % 变异概率选择，0和1之间
%染色体设置
lenchrom=ones(1,3);    % t1、t2、t3
bound=[38,59;26,37;33,44;];   % 数据范围
%---------------------------种群初始化------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness = [];                      %每一代种群的平均适应度
bestfitness = [];                     %每一代种群的最佳适应度
bestchrom = [];                       %适应度最好的染色体

%% 初始化种群
for i=1:sizepop
    % 随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound); % 编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）
    x=individuals.chrom(i,:);
    % 计算适应度
    individuals.fitness(i)=fun(x);   % 染色体的适应度 
end

%% 找最好的染色体
[bestfitness bestindex] = min(individuals.fitness);
bestchrom = individuals.chrom(bestindex,:);    % 最好的染色体
% 记录每一代进化中最好的适应度和平均适应度
trace = [bestfitness]; 

%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
    disp(['迭代次数：  ',num2str(i)])
    % 选择
    individuals=Select(individuals,sizepop); 
    % 交叉
    individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);

    % 计算适应度
    for j=1:sizepop
        x=individuals.chrom(j,:);        % 解码
        individuals.fitness(j)=fun(x);   % 染色体的适应度 
    end
%% 改进的GA
%% 清空环境变量
% clc,
clear % ,close all % 清除变量空间
warning off      % 消除警告
% feature jit off  % 加速代码执行
%% 遗传算法参数初始化
maxgen = 50;                      % 进化代数，即迭代次数
sizepop = 100;                     % 种群规模
pcross = [0.7];                    % 交叉概率选择，0和1之间
pmutation = [0.01];                 % 变异概率选择，0和1之间
delta = 0.1;
% 城市交通信号系统参数
C = 140;
L = 10;
load('data.mat')  % 包含交通流量q以及饱和流量xij
q = q./3600;      % 转化为秒s
xij = xij./3600;  % 转化为秒s
%染色体设置
lenchrom=ones(1,3);    % t1、t2、t3
bound=[38,59;26,37;33,44;];   % 数据范围
%---------------------------种群初始化------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness = [];                      %每一代种群的平均适应度
bestfitness = [];                     %每一代种群的最佳适应度
bestchrom = [];                       %适应度最好的染色体

%% 初始化种群
for i=1:sizepop
    % 随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound); % 编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）
    x=individuals.chrom(i,:);
    % 计算适应度
    individuals.fitness(i)=fun1(x);   % 染色体的适应度 
end

%% 找最好的染色体
[bestfitness bestindex] = min(individuals.fitness);
bestchrom = individuals.chrom(bestindex,:);    % 最好的染色体
% 记录每一代进化中最好的适应度和平均适应度
trace = [bestfitness]; 

%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
    disp(['迭代次数：  ',num2str(i)])
    % 选择
    individuals=Select1(individuals,sizepop); 
    % 交叉
    individuals.chrom=Cross1(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation1(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);

    % 计算适应度
    for j=1:sizepop
        x=individuals.chrom(j,:);        % 解码
        individuals.fitness(j)=fun1(x);   % 染色体的适应度 
    end
    fmax = max(individuals.fitness);     % 适应度最大值
    fmin = min(individuals.fitness);     % 适应度最小值
    favg = mean(individuals.fitness);  % 适应度平均值
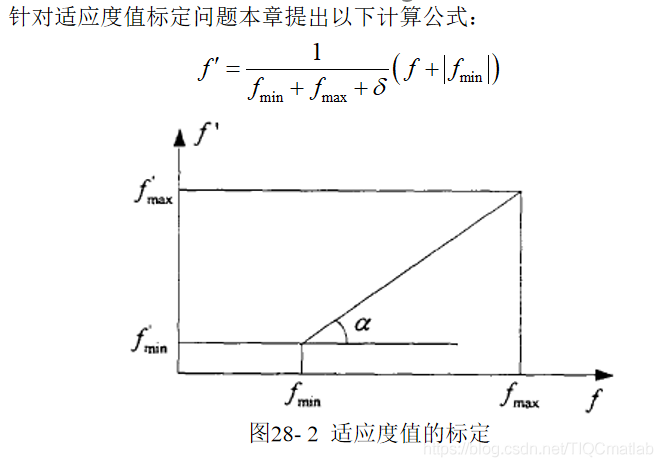
    individuals.fitness = (individuals.fitness + abs(fmin))./(fmax+fmin+delta); %适应度标定
    
  
    [newbestfitness,newbestindex]=min(individuals.fitness);
    [worestfitness,worestindex]=max(individuals.fitness);
   
    if bestfitness>newbestfitness
        bestfitness=newbestfitness;
        bestchrom=individuals.chrom(newbestindex,:);
    end

Three, running results

Insert picture description here

Four, remarks