Purpose: In the traditional vector cross product calculation, cross product is often encountered. Defined as a vector. The direction of this vector satisfies the right-hand rule. Its modulus size is generally ignored. So speculate.
Vector cross product definition:
Outer product (English: Cross product ), also known as vector product (English: Vector product t), is a binary operation on two vectors in three-dimensional space, with the symbol: × \times× means. can be defined as:
a → × b → = c → ( 1 ) \overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c} \space \space \space \space(1)a×b=c ( 1 )
Suppose two vectorsa → × b → \overrightarrow{a} \times \overrightarrow{b}a×bOuter product, its direction is c → \overrightarrow{c}c. Its direction is determined by the right-hand rule. The modulus length is equal to the area of the parallelogram of these two vector sides.
Its definition can also be written as:
a → × b → = ∣ a → ∣ ∣ b → ∣ sin ( θ ) n → ( 2 ) \overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}| |\overrightarrow{b}|sin(\theta)\overrightarrow{n} \space \space \space \space(2)a×b=∣a∣∣b∣ s in ( θ )n ( 2 )
θ \thetaθ is the angle between two vectors0 ≤ θ ≤ 180 0\le \theta \le 1800≤i≤180; ∣ a → ∣ ∣ b → ∣ |\overrightarrow{a}||\overrightarrow{b}| ∣a∣∣b∣Respectively , two vectorsa → b → \overrightarrow{a} \overrightarrow{b}abThe mold length. n → \overrightarrow{n}nis perpendicular to a → b → \overrightarrow{a} \overrightarrow{b}abThe normal vector of the plane where it satisfies the right-hand rule. As shown in the figure below:
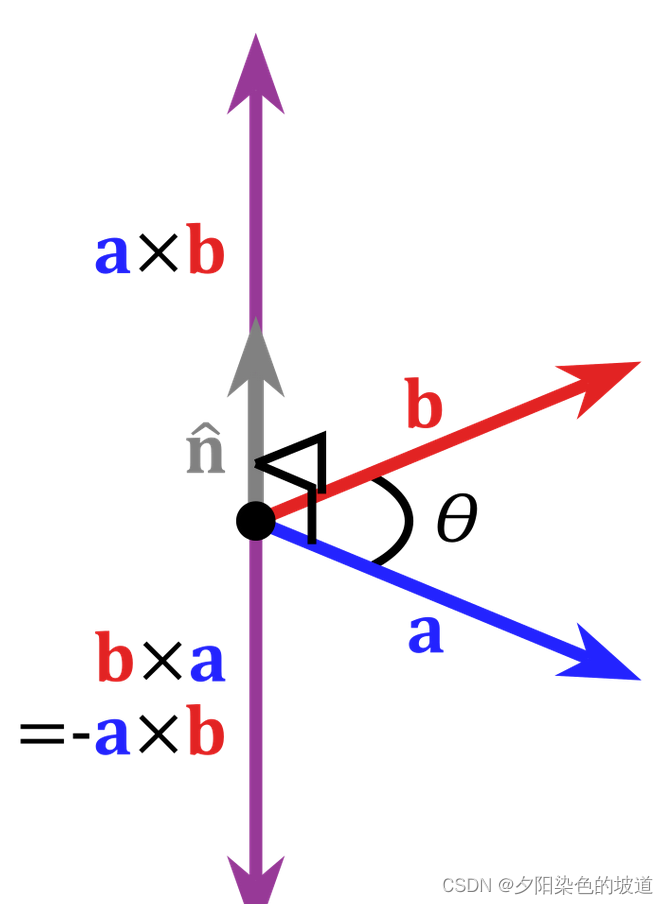
the above definition is easy to understand. But generally in algebra to calculate the cross product of two vectors, determinant calculation will be used. As a set of unit products ( i → , j → , k → ) (\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})(i,j,k);其中 a → = a 0 i → + a 1 j → + a 2 k → \overrightarrow{a}=a_0\overrightarrow{i}+a_1\overrightarrow{j}+a_2\overrightarrow{k} a=a0i+a1j+a2k; b → = b 0 i → + b 1 j → + b 2 k → \overrightarrow{b}=b_0\overrightarrow{i}+b_1\overrightarrow{j}+b_2\overrightarrow{k} b=b0i+b1j+b2k
When calculating the cross product of two vectors, the general algebraic method is:
a → × b → = ( a 0 i → + a 1 j → + a 2 k → ) × ( b → = b 0 i → + b 1 j → + b 2 k → ) = a 0 b 0 ( i → × i → ) + a 0 b 1 ( i → × j → ) + a 0 b 2 ( i → × k → ) + a 1 b 0 ( j → × i → ) + a 1 b 1 ( j → × j → ) + a 1 b 2 ( j → × k → ) + a 2 b 0 ( k → × i → ) + a 2 b 1 ( k → × j → ) + a 2 b 2 ( k → × k → ) ( 3 ) \overrightarrow{a} \times \overrightarrow{b} = (a_0\overrightarrow{i}+a_1\overrightarrow{j}+a_2\overrightarrow{k}) \times(\overrightarrow{b}=b_0\overrightarrow{i}+b_1\overrightarrow{j}+b_2\overrightarrow{k}) \\ = a_0b_0(\overrightarrow{i} \times \overrightarrow{i}) + a_0b_1(\overrightarrow{i} \times \overrightarrow{j}) + a_0b_2(\overrightarrow{i} \times \overrightarrow{k})+ \\ a_1b_0(\overrightarrow{j} \times \overrightarrow{i}) + a_1b_1(\overrightarrow{j} \times \overrightarrow{j}) + a_1b_2(\overrightarrow{j} \times \overrightarrow{k}) + \\ a_2b_0(\overrightarrow{k} \times \overrightarrow{i}) + a_2b_1(\overrightarrow{k} \times \overrightarrow{j}) + a_2b_2(\overrightarrow{k} \times \overrightarrow{k}) \space \space \space \space(3) a×b=(a0i+a1j+a2k)×(b=b0i+b1j+b2k)=a0b0(i×i)+a0b1(i×j)+a0b2(i×k)+a1b0(j×i)+a1b1(j×j)+a1b2(j×k)+a2b0(k×i)+a2b1(k×j)+a2b2(k×k) (3)
Because the basis vector ( i → , j → , k → ) (\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})(i,j,k) are perpendicular to each other and are unit vectors. 0 → \overrightarrow{0}0means all are 0 00的向量。所以得到:
i → × i → = 0 → ( 4 ) j → × j → = 0 → ( 5 ) k → × k → = 0 → ( 6 ) i → × j → = k → ( 7 ) j → × k → = i → ( 8 ) k → × i → = j → ( 9 ) \overrightarrow{i} \times \overrightarrow{i}= \overrightarrow{0} \space \space \space \space(4) \\ \overrightarrow{j} \times \overrightarrow{j}= \overrightarrow{0} \space \space \space \space(5) \\ \overrightarrow{k} \times \overrightarrow{k}=\overrightarrow{0} \space \space \space \space(6) \\ \overrightarrow{i} \times \overrightarrow{j}= \overrightarrow{k} \space \space \space \space(7) \\ \overrightarrow{j} \times \overrightarrow{k}= \overrightarrow{i} \space \space \space \space(8)\\ \overrightarrow{k} \times \overrightarrow{i}= \overrightarrow{j} \space \space \space \space(9) i×i=0 (4)j×j=0 (5)k×k=0 (6)i×j=k (7)j×k=i (8)k×i=j ( 9 )
will( 4 ) ( 5 ) ( 6 ) ( 7 ) ( 8 ) ( 9 ) (4) (5) (6) (7) (8) (9)( 4 ) ( 5 ) ( 6 ) ( 7 ) ( 8 ) ( 9 ) into formula( 3 ) (3)(3)得到如下:
a → × b → = − a 0 b 0 0 → + a 0 b 1 k → − a 0 b 2 j → − a 1 b 0 k → − a 1 b 1 0 → + a 1 b 2 i → + a 2 b 0 j → − a 2 b 1 i → − a 2 b 2 0 → = ( a 1 b 2 − a 2 b 1 ) i → + ( a 2 b 0 − a 0 b 2 ) j → + ( a 0 b 1 − a 1 b 0 ) k → ( 10 ) \overrightarrow{a} \times \overrightarrow{b} = -a_0b_0\overrightarrow{0}+a_0b_1\overrightarrow{k}-a_0b_2\overrightarrow{j} \\ - a_1b_0\overrightarrow{k}-a_1b_1\overrightarrow{0} +a_1b_2\overrightarrow{i} \\ +a_2b_0 \overrightarrow{j} - a_2b_1\overrightarrow{i} -a_2b_2\overrightarrow{0}\\ =(a_1b_2-a_2b_1)\overrightarrow{i} + (a_2b_0-a_0b_2)\overrightarrow{j} +(a_0b_1-a_1b_0)\overrightarrow{k} \space \space \space \space(10) a×b=−a0b00+a0b1k−a0b2j−a1b0k−a1b10+a1b2i+a2b0j−a2b1i−a2b20=(a1b2−a2b1)i+(a2b0−a0b2)j+(a0b1−a1b0)k (10)
Formula ( 10 ) (10)( 10 ) is expressed by determinant calculation in daily life. Use( i → , j → , k → ) (\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})(i,j,k) matrixremainder formulacalculation method. It is equivalent to algebraic computation.
a → × b → = [ i → j → k → a 0 a 1 a 2 b 0 b 1 b 2 ] = ( a 1 b 2 − a 2 b 1 ) i → + ( a 2 b 0 − a 0 b 2 ) j → + ( a 0 b 1 − a 1 b 0 ) k → \overrightarrow{a} \times \overrightarrow{b} =\begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow {k} \\ a_0& a_1 & a_2 \\ b_0& b_1 & b_2 \end{bmatrix} = (a_1b_2-a_2b_1)\overrightarrow{i} + (a_2b_0-a_0b_2)\overrightarrow{j} + (a_0b_1-a_1b_0)\overrightarrow {k}a×b=⎣
⎡ia0b0ja1b1ka2b2⎦
⎤=(a1b2−a2b1)i+(a2b0−a0b2)j+(a0b1−a1b0)k
Because it is a base vector, in Euclidean geometry, its expression is:
i → = [ 1 0 0 ] ; j → = [ 0 1 0 ] ; k → = [ 0 0 1 ] ( 11 ) \overrightarrow{i} =\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}; \overrightarrow{j}=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix};\overrightarrow{k}=\ begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \space \space \space \space(11)i=⎣
⎡100⎦
⎤;j=⎣
⎡010⎦
⎤;k=⎣
⎡001⎦
⎤ ( 11 )
so( 11 ) (11)( 11 ) into( 10 ) (10)(10)得到:
a → × b → = [ a 1 b 2 − a 2 b 1 a 2 b 0 − a 0 b 2 a 0 b 1 − a 1 b 0 ] ( 12 ) \overrightarrow{a} \times \overrightarrow{b} = \begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} \space \space \space \space(12) a×b=⎣
⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦
⎤ (12)
The above is an expression based on the basis vector, which corresponds to the above formula, so it can be obtained:
a → × b → = ∣ a → ∣ ∣ b → ∣ sin ( θ ) n → = [ a 1 b 2 − a 2 b 1 a 2 b 0 − a 0 b 2 a 0 b 1 − a 1 b 0 ] ( 13 ) \overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|sin (\theta)\overrightarrow{n} =\begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} \space \space \space \space(13)a×b=∣a∣∣b∣ s in ( θ )n=⎣
⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦
⎤ (13)
In some applications, often vector representations are transformed into matrix operations. So (13) formula can represent the multiplication of matrix and vector.
a → × b → = ∣ a → ∣ ∣ b → ∣ sin ( θ ) n → = [ a 1 b 2 − a 2 b 1 a 2 b 0 − a 0 b 2 a 0 b 1 − a 1 b 0 ] = [ 0 − a 2 a 1 a 2 0 − a 0 − a 1 a 0 0 ] [ b 0 b 1 b 2 ] = a → × b → ( 14 ) \overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|sin(\theta)\overrightarrow{n} =\begin{bmatrix} a_1b_2-a_2b_1 \\ a_2b_0-a_0b_2 \\ a_0b_1-a_1b_0 \end{bmatrix} = \begin{bmatrix} 0 & -a_2 & a_1 \\ a_2& 0 & -a_0 \\ -a_1& a_0 & 0 \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \end{bmatrix} = \overrightarrow {a} \times \overrightarrow{b} \space \space \space \space(14)a×b=∣a∣∣b∣ s in ( θ )n=⎣
⎡a1b2−a2b1a2b0−a0b2a0b1−a1b0⎦
⎤=⎣
⎡0a2−a1−a20a0a1−a00⎦
⎤⎣
⎡b0b1b2⎦
⎤=a×b (14)
The cross product of two vectors is only defined in three dimensions. Not defined in two dimensions.
The following introduces the relationship between the determinant of a vector and the area of a parallelogram formed by a vector.
Suppose a → , b → \overrightarrow{a} ,\overrightarrow{b}a,bis a two-dimensional vector. That's easy to explain. So the plot looks like this:
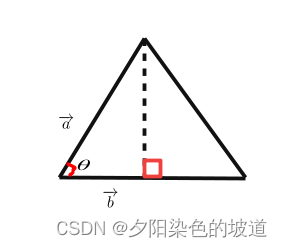
Calculate the triangle area as:
∣ area ∣ = 1 2 ∣ a → ∣ ∣ b → ∣ sin ( θ ) ( 15 ) |area|=\cfrac{1}{2}|\overrightarrow{a}||\overrightarrow{b }|sin(\theta) \space \space \space \space(15)∣area∣=21∣a∣∣b∣ s in ( θ ) ( 15 )
Transform the expression, because sin ( θ ) sin(\theta)s in ( θ ) is not easy to calculate, you need to calculatecos ( θ ) cos(\theta)cos ( θ ) .
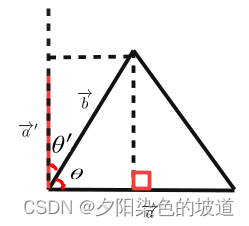
其中 ∣ a → ′ ∣ = ∣ a → ∣ |\overrightarrow{a}'|=|\overrightarrow{a}| ∣a′∣=∣a∣; ∣ b → ∣ s i n ( θ ) = ∣ b → ′ ∣ c o s ( θ ′ ) |\overrightarrow{b}|sin(\theta)=|\overrightarrow{b}'|cos(\theta') ∣b∣ s in ( θ )=∣b′ ∣cos(i′);
∣ a r e a ∣ = 1 2 ∣ a → ∣ ∣ b → ∣ s i n ( θ ) = 1 2 ∣ b → ∣ ∣ a → ∣ c o s ( θ ′ ) ( 16 ) |area|=\cfrac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|sin(\theta)=\cfrac{1}{2}|\overrightarrow{b}||\overrightarrow{a}|cos(\theta') \space \space \space \space(16) ∣area∣=21∣a∣∣b∣ s in ( θ )=21∣b∣∣a∣ cos ( i′ )(16)
in whichθ ′ + θ = 90 \theta'+\theta=90i′+i=90.且 ∣ a → ′ ∣ = ∣ a → ∣ |\overrightarrow{a}'|=|\overrightarrow{a}| ∣a′∣=∣a∣ , it is easy to get the simplification of the formula. Simplifying the above equation is:
∣ area ∣ = 1 2 ∣ b → ∣ ∣ a → ′ ∣ cos ( θ ′ ) = 1 2 b → ⋅ a → ′ = 1 2 a → ′ ⋅ b → ( 17 ) |area|=\cfrac{1}{2}|\overrightarrow{b}||\overrightarrow{a}'|cos(\theta')=\cfrac{1}{2}\overrightarrow{b } \cdot \overrightarrow{a}'=\cfrac{1}{2}\overrightarrow{a}' \cdot \overrightarrow{b} \space \space \space \space(17)∣area∣=21∣b∣∣a′ ∣cos(i′)=21b⋅a′=21a′⋅b (17)
because a → ′ \overrightarrow{a}'a′ is viaa → \overrightarrow{a}aRotate 90 degrees to get, as shown below.
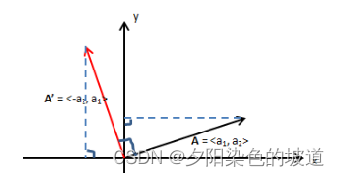
So suppose a → = [ a 0 a 1 ] \overrightarrow{a}=\begin{bmatrix} a_0 \\ a_1 \end{bmatrix}a=[a0a1] 得到 a → ′ = [ − a 1 a 0 ] \overrightarrow{a}'=\begin{bmatrix} -a_1 \\ a_0 \end{bmatrix} a′=[−a1a0]
因此得到公式:
2 ∣ a r e a ∣ = a → ′ ⋅ b → = [ − a 1 a 0 ] ⋅ [ b 0 b 1 ] = a 0 b 1 − a 1 b 0 ( 18 ) 2|area|=\overrightarrow{a}' \cdot \overrightarrow{b}=\begin{bmatrix} -a_1 \\ a_0 \end{bmatrix} \cdot \begin{bmatrix} b_0 \\ b_1 \end{bmatrix} = a_0b_1-a_1b_0 \space \space \space \space(18) 2∣area∣=a′⋅b=[−a1a0]⋅[b0b1]=a0b1−a1b0 (18)
It can be seen that the determinant is an expression of area.
2 ∣ area ∣ = ∣ a 0 a 1 b 0 b 1 ∣ 2|area|=\begin{vmatrix} a_0 & a_1 \\ b_0 & b_1 \end{vmatrix}2∣area∣=∣
∣a0b0a1b1∣
∣