Instituto de Tecnología de Harbin 2022 Experimento de aprendizaje automático 1: Ajuste de curvas

Los requisitos de este experimento son bastante claros (en comparación con el semestre anterior). Este blog está implementado en python, se usa la biblioteca de computación científica numpyy se usa el dibujo matplotlib.pyplot. Para simplificar, importe lo siguiente al comienzo del archivo:

import numpy as np
import matplotlib.pyplot as plt

Las funciones numpy utilizadas en este experimento

Generalmente numpyabreviado como np(importar numpy como np). La siguiente es una breve introducción a las funciones numpy utilizadas en el experimento. El siguiente código debe agregarse en la parte superior import numpy as np.

np.matriz

Esta función devuelve un numpy.ndarrayobjeto, que puede entenderse como una matriz multidimensional (en este experimento, solo se usará unidimensional (puede considerarse como un vector de columna) y bidimensional (matriz). Use minúsculas $Xx$ es un vector columna,$A$ representa una matriz. A.TsignificaAATranspuesta de$A.$Las operaciones en paresndarrayson generalmente por elementos.

>>> x = np.array([1,2,3])
>>> x
array([1, 2, 3])
>>> A = np.array([[2,3,4],[5,6,7]])
>>> A
array([[2, 3, 4],
       [5, 6, 7]])
>>> A.T # 转置
array([[2, 5],
       [3, 6],
       [4, 7]])
>>> A + 1
array([[3, 4, 5],
       [6, 7, 8]])
>>> A * 2
array([[ 4,  6,  8],
       [10, 12, 14]])

np.aleatorio

np.randomEl módulo contiene varias funciones para generar números aleatorios. En este experimento, se utilizan parámetros de inicialización aleatorios (método de descenso de gradiente) para agregar ruido a los datos.

>>> np.random.rand(3, 3) # 生成3 * 3 随机矩阵，每个元素服从[0,1)均匀分布
array([[8.18713933e-01, 5.46592778e-01, 1.36380542e-01],
       [9.85514865e-01, 7.07323389e-01, 2.51858374e-04],
       [3.14683662e-01, 4.74980699e-02, 4.39658301e-01]])
      
>>> np.random.rand(1) # 生成单个随机数
array([0.70944563])
>>> np.random.rand(5) # 长为5的一维随机数组
array([0.03911319, 0.67572368, 0.98884287, 0.12501456, 0.39870096])
>>> np.random.randn(3, 3) # 同上，但每个元素服从N(0, 1)（标准正态）

función matemática

Solo usado en este experimento np.sin. Estas funciones matemáticas np.ndarrayoperan por elementos:

>>> x = np.array([0, 3.1415, 3.1415 / 2]) # 0, pi, pi / 2
>>> np.round(np.sin(x)) # 先求sin再四舍五入: 0, 0, 1
array([0., 0., 1.])

Además, hay np.logfunciones similares np.expa la biblioteca de python math(solo para operaciones de elementos en matrices multidimensionales).

np.punto

Devuelve el producto de dos matrices. Consistente con la multiplicación de matrices en álgebra lineal. Se requiere que las columnas de la primera matriz sean iguales al número de filas de la segunda matriz. En particular, cuando uno de ellos es un arreglo unidimensional, la forma se adapta automáticamente a $norte\times 1$ o$1\times norte\_$

>>> x = np.array([1,2,3]) # 一维数组
>>> A = np.array([[1,1,1],[2,2,2],[3,3,3]]) # 3 * 3矩阵
>>> np.dot(x,A)
array([14, 14, 14])
>>> np.dot(A,x)
array([ 6, 12, 18])

>>> x_2D = np.array([[1,2,3]]) # 这是一个二维数组（1 * 3矩阵）
>>> np.dot(x_2D, A) # 可以运算
array([[14, 14, 14]])
>>> np.dot(A, x_2D) # 行列不匹配
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<__array_function__ internals>", line 5, in dot
ValueError: shapes (3,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)

np.ojo

np.eye(n)Devuelve una matriz unitaria de orden n.

>>> A = np.eye(3)
>>> A
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Correlación de álgebra lineal

np.linalges una biblioteca relacionada con el álgebra lineal.

>>> A
array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])
>>> np.linalg.inv(A) # 求逆（本实验不考虑逆不存在）
array([[1.        , 0.        , 0.        ],
       [0.        , 0.5       , 0.        ],
       [0.        , 0.        , 0.33333333]])
>>> x = np.array([1,2,3])
>>> np.linalg.norm(x) # 返回向量x的模长（平方求和开根号）
3.7416573867739413
>>> np.linalg.eigvals(A) # A的特征值
array([1., 2., 3.])

Generar datos

Generar los datos requiere agregar ruido (error). El ejemplo dado en clase es la función seno, también usamos la función seno estándar $y=\mathrm{pecado}x($ después de agregar ruido, es$y=\mathrm{pecado}X+ϵ,$ con$ϵ\sim norte(0,{pags}^2)$, ya que$\mathrm{pecado}$El valor máximo de$x$$1$ , establecemos la varianza del error para que sea menor, aquí se establece en$\frac{}{25}$).

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1], 默认为(0, 10)
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    # np.random.rand 产生[0, 1)的均匀分布，再根据l, r缩放平移
    # 这里sort是为了画图时不会乱，可以去掉sorted试一试
    x = sorted(np.random.rand(N) * (r - l) + l)
	
	# np.random.randn 产生N(0,1)，除以5会变为N(0, 1 / 25)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

El conjunto de datos resultante tiene un punto en un plano por fila. Los datos resultantes se ven así:

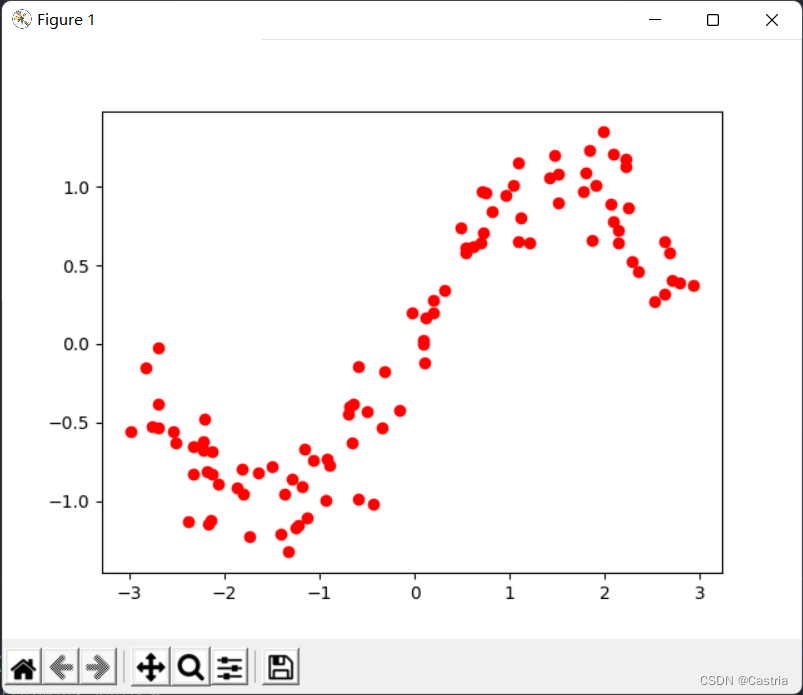
vagamente en la forma de una función seno. El código que produce la imagen de arriba es el siguiente:

dataset = get_dataset(bound = (-3, 3))
# 绘制数据集散点图
for [x, y] in dataset:
    plt.scatter(x, y, color = 'red')
plt.show()

Ajuste de mínimos cuadrados

A continuación, utilizamos cuatro métodos (mínimos cuadrados, término regular/regresión de cresta, descenso de gradiente, gradiente conjugado) para ajustar las sinusoides perturbadas anteriores con polinomios.

Derivación de soluciones analíticas

Simplemente recuerda el principio del método de los mínimos cuadrados: ahora queremos usar un mmPolinomio$f\; (\; x\; )\; de\; grado\; m$
$$f\left(x\right)={en}_{}+{en}_{}X+{en}_{}{X}^2+...+{en}_{}{X}^m$$
para aproximar la función verdadera$y=\mathrm{pecado}x$ Nuestro objetivo es minimizar los conjuntos de datos$($$(X_{},y_{}),(X_{},y_{}),...,(X_{},y_{})$ sobre la pérdida$L$ (pérdida), donde la función de pérdida toma el error al cuadrado:
$$L=\sum _{yo=1}[y_{}-f(x_{}){]}^2$$
Para encontrar los parámetros${en}_{},{en}_{},...,{en}_{},$ necesitamos encontrar la pérdida$L$ relacionado con w 0 , w 1 , . . . , wm w_0, w_1,...,w_m${en}_{},{en}_{},...,{en}_{}$derivado de . Por conveniencia, usamos la notación de álgebra lineal:
$$X={⎝\begin{array}{ccccc}1& X_{}& X_1^{}& \cdots & X_1^{}\\ 1& X_{}& X_2^{}& \cdots & X_2^{}\\ ⋮& & & & ⋮\\ & X_{}& X_{norte}^{}& & X_{norte}^{}\end{array}⎠}_{N\times (metro+1},Y={⎝\begin{array}{c}{y}_{}\\ y_{}\\ ⋮\\ y_{}\end{array}⎠}_{norte\times },En={⎝\begin{array}{c}{en}_{}\\ {en}_{}\\ ⋮\\ {en}_{}\end{array}⎠}_{(metro+1)\times }$$
Bajo esta representación,$$($$
$$⎝\begin{array}{c}f\left(x_{}\right)\\ f\left(x_{}\right)\\ ⋮\\ f(x_{}\end{array}⎠=XW.$$
Si tienes dudas, puedes comprobarlo tú mismo con la multiplicación de matrices$$.$$Continuando, la suma de los términos de error se puede expresar como
$$⎝\begin{array}{c}f\left(x_{}\right)-y_{}\\ f\left(x_{}\right)-y_{}\\ ⋮\\ f\left(x_{}\right)-y_{}\end{array}⎠=XW-Y.\; Porlo$$
tanto, la función de pérdida
$$L=(XA\_-Y{)}^T(XAN-Y).$$
(Para encontrar el vector$XX=(X_{},X_{},...,X_{}{)}^{}$La suma de los cuadrados de las componentes de${}^T$$Xx$ es el producto interno, es decir,${XX}^{T}Xx.$ )
para obtener la$L$ más pequeño$W$ (este$W$ es unvector columna), necesitamosEncuentre la derivada parcial de$L$$0:$
$$\begin{array}{rl}\frac{\partial L}{\partial W}& =\frac{}{\partial W}[(XW-Y{)}^T(XAN-Y)]\\ & =\frac{}{\partial W}[(W^{TX}{\_}^T-Y^T\left)\right(XAN-Y)]\\ & =\frac{}{\partial W}({w.}^{TX}{\_}^{T}XAN-{En}^{TX}{\_}^{}TY{}^{\_}-Y^{T}XAN+Y^{}TY){}^{\_}\\ & =\frac{}{\partial W}({w.}^{TX}{\_}^{T}XAN-2{años}^{T}XAN+Y^{T}Y)(fácil\; de\; verificar,{En}^{TX}{\_}^{}TY{}^{\_}=Y^{T}XW,por\; lo\; tanto\; se\; pueden\; combinar)\\ & =2X\_{}^{T}XAN-2X\_{}^{}\end{array}$$
Descripción:
(1) De la línea 3 a la línea 4, debido a ${En}^{TX}{\_}^{T}Y$和$Y^{T}XW$son todos los números (o$1\times 1$ matriz), los dos se transponen entre sí, por lo que los valores son los mismos y se pueden combinar en un solo elemento.
(2) Derivación de la matriz de la fila 4 a la fila 5, el primer término$\frac{}{\partial W}\left({w.}^T\right(X^{T}X\left)W\right)$se trata de$La\; forma\; cuadrática\; de\; W$ , su derivada es$2X\_{}^{T}XW.($
3) Para el término primario$-2{años}^{La\; derivación\; de\; T}XW$, si la derivación según el campo de números reales, debería ser$-2{años}^{T}X.Pero$verifique y descubra que el tipo de matriz no es correcto, debe hacer una transposición, se convierte en$-2X^{T}Y.$

El álgebra lineal de matrices no se ha enseñado sistemáticamente en la clase, solo para explicar lo que aparece aquí. ( No lo haré si hay más )
Deje que la derivada parcial sea 0, obtenga
$$X^{T}XAN=Y^{T}X,$$
multiplicar por la izquierda$\left(X^{TX}\right)\_{}^{-1}$ ($X^{}$Consulte la nota complementaria a continuación para conocer la reversibilidad de${}^T$$X$
$$En=\left(X^{TX}\right)\_{}^{-1}{X}^{T}Y.$$
Este es el$$WW$$$Para\; la\; solución\; analítica\; de\; W$ , solo necesitamos llamar a la función para calcular este valor.

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)

Explique un poco el código: la primera línea genera el XX acordado anteriormenteLa matriz$X$dataset[:,0] , que es la columna 0 del conjunto de datos$(X_{},X_{},...,X_{}{)}^T$ ; la segunda línea es$Matriz\; Y$ ; la tercera fila devuelve la solución analítica anterior. (Si no está familiarizado con la sintaxis onumpylas bibliotecas de Python, es bastante hostil)

Simplemente verificamos el resultado de la función que hemos completado: Para ello, primero escribimos una drawfunción para convertir el WW obtenidoEl polinomiof ( x ) f(x)$correspondiente\; a\; W$Dibuja$f$$($$x$$)$pyplot en la imagen de la biblioteca:

'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

Entonces la función principal:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 最小二乘
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')
    
	# 绘制图像
    plt.legend()
    plt.show()

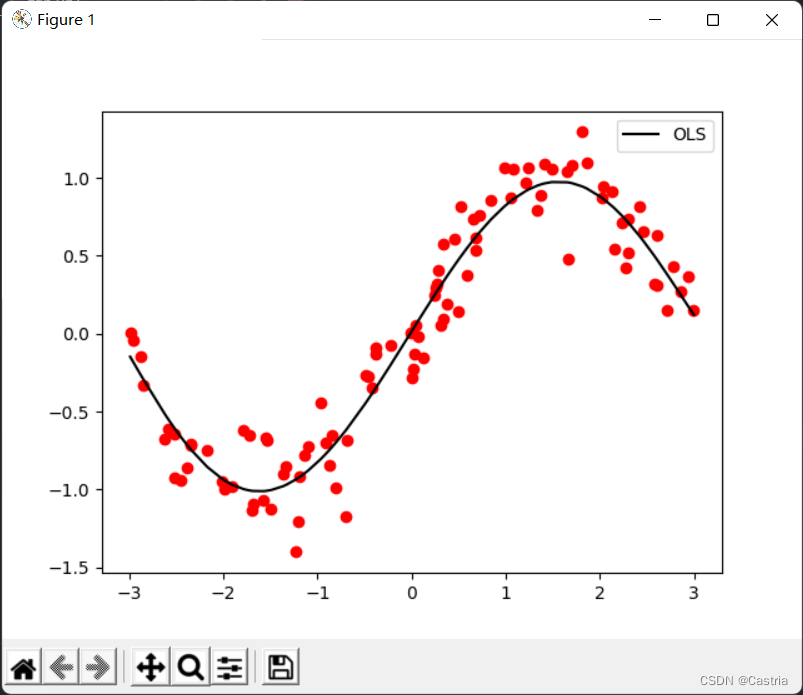
Se puede ver que el efecto del ajuste polinomial de quinto grado es bastante bueno (el conjunto de datos se genera aleatoriamente cada vez, por lo que es diferente de la primera imagen).

A partir de todo el código de esta parte, ya no se describen las siguientes funciones del mismo nombre:

import numpy as np
import matplotlib.pyplot as plt

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1]
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    x = sorted(np.random.rand(N) * (r - l) + l)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)
'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

if __name__ == '__main__':

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')

    plt.legend()
    plt.show()

Instrucciones complementarias

Hay una pieza menos rigurosa arriba: para una matriz $Para\; X$ ,$X^{TX}$ no es necesariamente reversible$.$En este experimento, sin embargo, se puede demostrar que es una matriz invertible. Dado que esta clase no es una clase de álgebra lineal, no dedicaremos demasiado espacio a esto, solo un breve recordatorio:
(1)$X$ es un$norte\times (metro+1)$ de la matriz. donde el número de datos es$N$ es mucho mayor que el polinomio grado$m$ , hay$norte>metro+1;$
(2) Para ilustrar$X^{T}X$es invertible, necesito explicar$\left(X^{TX}\right)\_{}_{(metro+1)\times (metro+1}$Rango completo, es decir, $R\left(X^{TX}\right)\_=metro+1;$
(3) En álgebra lineal, hemos probado que$R\left(X\right)=R\left(X^t\right)=R\left(X^{TX}\right)\_=R\left(X{X}^t\right);$
(4)$X$ es unamatriz de Vandermondecuyo rango es igual a$mi\{n,metro+1\}=metro+1.$

Agregar término de regularización (regresión de cresta)

El método de mínimos cuadrados es propenso al sobreajuste. Para ilustrar este defecto, usamos los primeros 50 puntos del conjunto de datos generado para el entrenamiento (para que el muestreo no sea lo suficientemente uniforme, aquí es solo para ilustrar el sobreajuste), obtenemos los parámetros y luego dibujamos la imagen de la función completa para comprobar el efecto de ajuste:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 取前50个点进行训练
    coef1 = fit(dataset[:50], m = 3)
    # 再画出整个数据集上的图像
    draw(dataset, coef1, color = 'black', label = 'OLS')

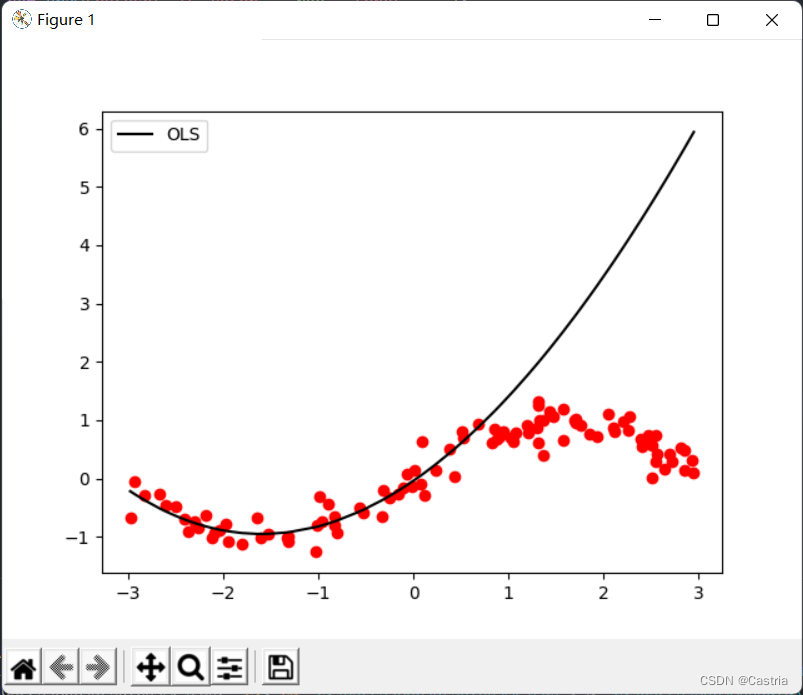
Sobreajuste en mmEsto es especialmente grave cuando$m$$metro=3$ en punto). A medida que aumenta el grado del polinomio, para estar lo más cerca posible del conjunto de datos dado, la magnitud de los coeficientes calculados será cada vez mayor y el rendimiento en muestras no vistas será peor. Como se muestra arriba, puede ver que el ajuste está en los primeros 50 puntos (aproximadamente en la abscisa$[-3,0]$ ) es muy bueno; en el equipo de prueba el rendimiento es muy pobre ($[0,3]$ ). Para evitar el sobreajuste, se puede introducir un término de regularización. En este momento, la función de pérdida$L$变为
$$L=(XA\_-Y{)}^T(XAN-Y)+\lambda ||W|{|}_2^{}$$
donde $||\cdot |{|}_2^{}$Indica $L_{}$El cuadrado de la norma, en este caso ${En}^{}TW;{}^{\_}\lambda$ es el coeficiente de regularización. Esta fórmula también se llama Regresión de Ridge. Su idea es tener en cuenta la función de pérdida y el parámetro resultante$Módulo\; de\; longitud\; de\; W$ (en$L_{}$norma), previniendo $El\; parámetro\; en\; W$ es demasiado grande.

Por ejemplo (los números se componen aleatoriamente): cuando el coeficiente de regularización es $1$ , si el error cuadrático del esquema 1 en el conjunto de datos es$\mathrm{0,5},$ en este momento$En=(100,-200,300,150{)}^T$ ; el error cuadrático del esquema 2 en el conjunto de datos es$10,$ en este momento$En=(1,-3,2,1)$ , luego elegimos$W.$ Coeficiente de regularización$\lambda$$\lambda$ caracteriza esto paraWWLa importancia de la longitud del módulo$W$ : λ \lambdaCuanto mayor$sea\; \lambda$$Cuanto\; mayor\; sea\; la\; longitud\; del\; módulo\; de\; W$ , mayor será la penalización. Cuando$yo=0,\; la$ regresión de cresta se convierte en el método de mínimos cuadrados ordinarios. Similar a la regresión de cresta es LASSO, que reemplaza el término de regularización con$L_{}$norma.

Repitiendo la derivación anterior, podemos obtener la solución analítica como
$$En=(X^{TX}\_+\lambda E{\_}_{metro+}{)}^{-1}{X}^{T}Y.$$
donde$$E$$$Y_{metro+}$es $metro+$Matriz unitaria de$primer\; orden.$Es fácil obtener$(X^{TX}\_+\lambda E{\_}_{metro+})$ también es reversible.

Esta parte del código es la siguiente.

'''
岭回归求解析解, m 为多项式次数, l 为 lambda 即正则项系数
岭回归误差为 (XW - Y)^T*(XW - Y) + λ(W^T)*W
- dataset 数据集
- m 多项式次数, 默认为 5
- l 正则化参数 lambda, 默认为 0.5
'''
def ridge_regression(dataset, m = 5, l = 0.5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + l * np.eye(m + 1)), X.T), Y)

La comparación de los dos métodos es la siguiente:

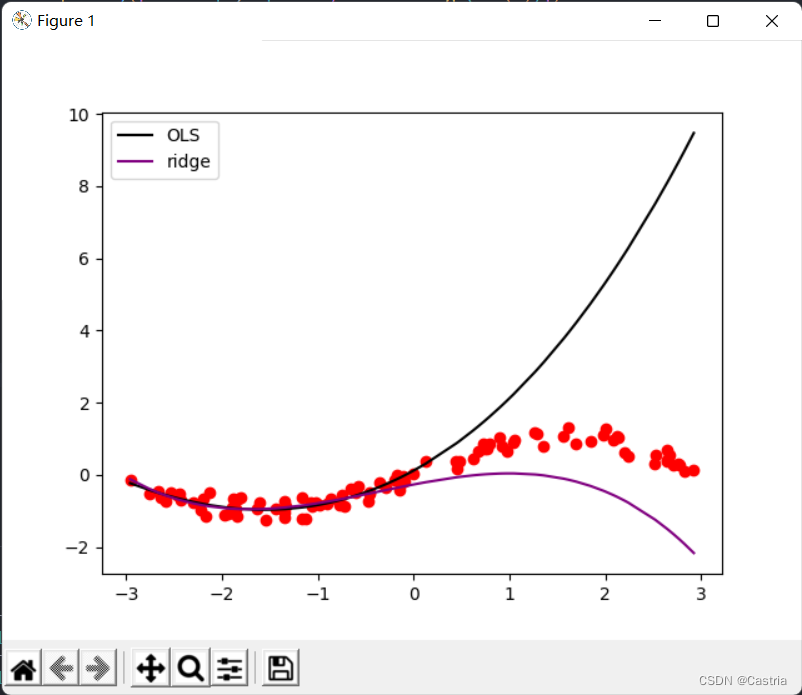
puede verse a partir de la comparación que la regresión de la cresta reduce significativamente el sobreajuste (en este momento $metro=3,yo=0.3$ ).

Descenso de gradiente

El descenso de gradiente no es la mejor manera de resolver este problema y puede fallar fácilmente en la convergencia. Primero introduzca brevemente la idea básica del método de descenso de gradiente: si queremos encontrar la función compleja f ( x ) f(x)El valor mínimo (punto máximo) de$f$$($$x$$)$$x$ puede ser un vector, etc.), es decir,
$$X_{}=\underset{X}{\mathrm{argumento}}f\left(x\right)$$
gradiente de descenso repite las siguientes operaciones:
(0) (al azar) inicializar$X_{}(t=0)$ ;
(1) Sea$f\left(x\right)$ en$X_{}$gradiente en (cuando $Cuando\; x$ es unidimensional, es la derivada)$\nabla f\left(x_{}\right)$；
（2）$X_{t+}=X_{}-\eta \nabla f\left(x_{}\right)$
(3) Si$X_{t+}$con $X_{}$Si hay poca diferencia (alcanza el rango preestablecido) o el número de iteraciones alcanza el límite superior preestablecido, detenga el algoritmo; de lo contrario, repita (1) (2).

Entre ellos η\ eta$\eta$ es la tasa de aprendizaje, que determina el tamaño del paso del descenso del gradiente.
El siguiente es un método de descenso de gradiente para encontrar$y=X^{}$Ejemplo de programa para el punto mínimo de${}^{2\; :}$

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return x ** 2

def draw():
    x = np.linspace(-3, 3)
    y = f(x)
    plt.plot(x, y, c = 'red')

cnt = 0
# 初始化 x
x = np.random.rand(1) * 3
learning_rate = 0.05

while True:
    grad = 2 * x
    # -----------作图用，非算法部分-----------
    plt.scatter(x, f(x), c = 'black')
    plt.text(x + 0.3, f(x) + 0.3, str(cnt))
    # -------------------------------------
    new_x = x - grad * learning_rate
    # 判断收敛
    if abs(new_x - x) < 1e-3:
        break

    x = new_x
    cnt += 1

draw()
plt.show()

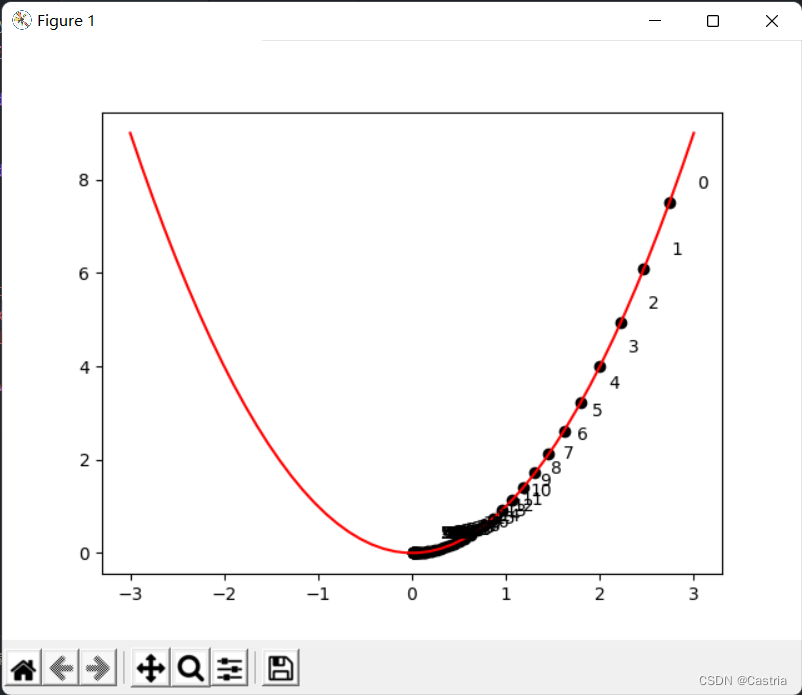
La imagen de arriba indica $x$ A medida que evoluciona la iteración, puede ver$x$ sigue acercándose a cero a lo largo del semieje positivo. Cabe señalar que la tasa de aprendizaje no puede ser demasiado grande (aunque en el programa anterior, la tasa de aprendizaje se establece un poco pequeña), debe ajustarse manualmente, de lo contrario, es fácil de imaginar,$x$ oscila de un lado a otro en los semiejes positivo y negativo, lo que dificulta la convergencia.

En mínimos cuadrados, la función que necesitamos optimizar es la función de pérdida
$$L=(XA\_-Y{)}^T(XAN-Y)A$$
continuación resolvemos el problema con gradiente descendente. En la derivación anterior,
$$\begin{array}{r}\frac{\partial L}{\partial W}=2X\_{}^{T}XAN-2X\_{}^{}\end{array},$$
por lo que cada vez que realizamos una iteración en$W$ resta este gradiente hasta el parámetro$W$ converge. Sin embargo, después de los experimentos, el error cuadrático hará que el gradiente sea demasiado grande y el proceso no pueda converger. Por lo tanto, se usa el error cuadrático medio (MSE) para reemplazarlo, que consiste en dividir la fórmula original por$norte$ :

'''
梯度下降法(Gradient Descent, GD)求优化解, m 为多项式次数, max_iteration 为最大迭代次数, lr 为学习率
注: 此时拟合次数不宜太高(m <= 3), 且数据集的数据范围不能太大(这里设置为(-3, 3)), 否则很难收敛
- dataset 数据集
- m 多项式次数, 默认为 3(太高会溢出, 无法收敛)
- max_iteration 最大迭代次数, 默认为 1000
- lr 梯度下降的学习率, 默认为 0.01
'''
def GD(dataset, m = 3, max_iteration = 1000, lr = 0.01):
    # 初始化参数
    w = np.random.rand(m + 1)

    N = len(dataset)
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = dataset[:, 1]

    try:
        for i in range(max_iteration):
            pred_Y = np.dot(X, w)
            # 均方误差（省略系数2）
            grad = np.dot(X.T, pred_Y - Y) / N
            w -= lr * grad
    '''
    为了能捕获这个溢出的 Warning，需要import warnings并在主程序中加上：
    warnings.simplefilter('error')
    '''
    except RuntimeWarning:
        print('梯度下降法溢出, 无法收敛')

    return w

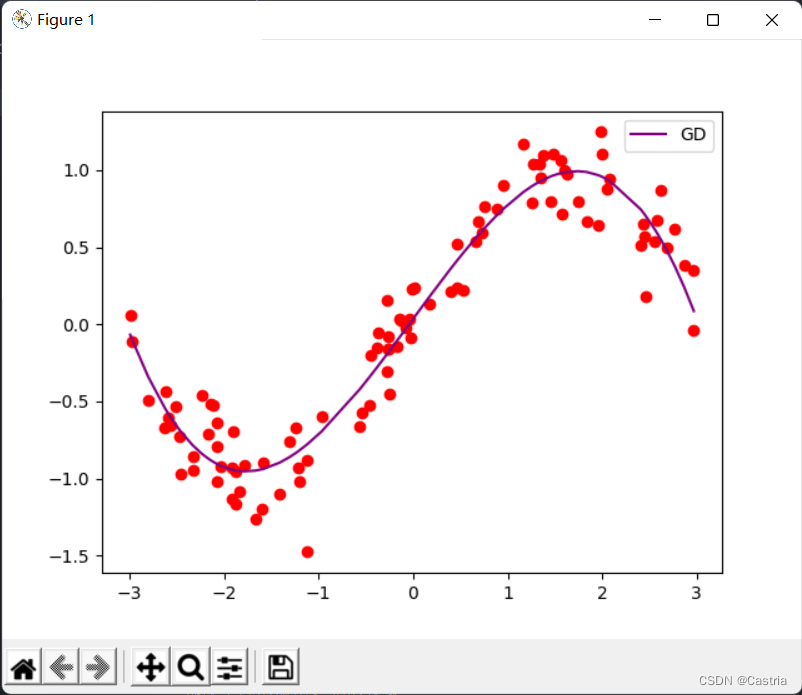
En este momento si $Si\; m$ se establece un poco más grande (digamos 4), el gradiente se desbordará durante la iteración, haciendo que los parámetros no puedan converger. Al converger, el efecto de ajuste está bien:

método de gradiente conjugado

Los gradientes conjugados se pueden usar para resolver la forma $AXX=b$Sistema de ecuaciones para$b$$f\left(Xx\right)=\frac{}{2}{XX}^{TA}\_XX-{bb}^{T}XX+c.$ (Se puede demostrar que para$A$ , los dos son equivalentes) donde$A$ es unamatrizdefinida positivaEn este problema, pedimos resolver$$X^{T}XAN=Y^{T}X,$$
entonces$A_{(metro+1)\times (metro+1}=X^{TX},\_bb=Y^{T.}$ Si queremos agregar un término regular, se convierte en la solución$.$
$$(X^{TX}\_+\lambda E)W=Y^{T}X.,$$
déjame explicarte:$X^{TX}no$es necesariamente definido positivo, pero debe ser semidefinido positivo (ver). Pero en el experimento básicamente no tenemos que preocuparnos por este problema, porque$X^{}Es$${}^{muy\; probable\; que\; TX}$ sea definido positivo, solo agregamos una aserción al código y no prestamos mucha atención a esta condición.
La idea del método del gradiente conjugado y el proceso de prueba son relativamente largos. Puede consultaresta serie. Aquí solo se dan los pasos del algoritmo (al comienzo del tercer artículo vinculado anteriormente):

(0) Inicializar $X_{(0};$
(1) Inicializar$d_{(0}=r_{(0}=b-una{x}_{(0};$
(2)令$$a_{(yo}=\frac{r_{\left(yo\right)}^{}{r}_{(yo}}{d_{\left(yo\right)}^{}una{d}_{(yo}};$$
（3）迭代$X_{(yo+1}=X_{(yo}+a_{(yo}{d}_{(yo};$
（4）令$r_{(yo+1}=r_{(yo}-a_{(yo}una{d}_{(yo};$
（5）令$$b_{(yo+1}=\frac{r_{(yo+1)}^{}{r}_{(yo+1}}{r_{\left(yo\right)}^{}{r}_{(yo}},d_{(yo+1}=r_{(yo+1}+b_{(yo+1}{d}_{(yo}.$$
（6）当$\frac{||r_{(yo}}{||r_{(0}||}<ϵ$ , detenga el algoritmo; de lo contrario, continúe iterando desde (2). $ϵ$ es un pequeño valor preestablecido, tomo aquí$10^{-5.}A\; continuación\; seguimos\; este\; proceso\; para$
implementar el código:

'''
共轭梯度法(Conjugate Gradients, CG)求优化解, m 为多项式次数
- dataset 数据集
- m 多项式次数, 默认为 5
- regularize 正则化参数, 若为 0 则不进行正则化
'''
def CG(dataset, m = 5, regularize = 0):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    A = np.dot(X.T, X) + regularize * np.eye(m + 1)
    assert np.all(np.linalg.eigvals(A) > 0), '矩阵不满足正定!'
    b = np.dot(X.T, dataset[:, 1])
    w = np.random.rand(m + 1)
    epsilon = 1e-5

    # 初始化参数
    d = r = b - np.dot(A, w)
    r0 = r
    while True:
        alpha = np.dot(r.T, r) / np.dot(np.dot(d, A), d)
        w += alpha * d
        new_r = r - alpha * np.dot(A, d)
        beta = np.dot(new_r.T, new_r) / np.dot(r.T, r)
        d = beta * d + new_r
        r = new_r
        # 基本收敛，停止迭代
        if np.linalg.norm(r) / np.linalg.norm(r0) < epsilon:
            break
    return w

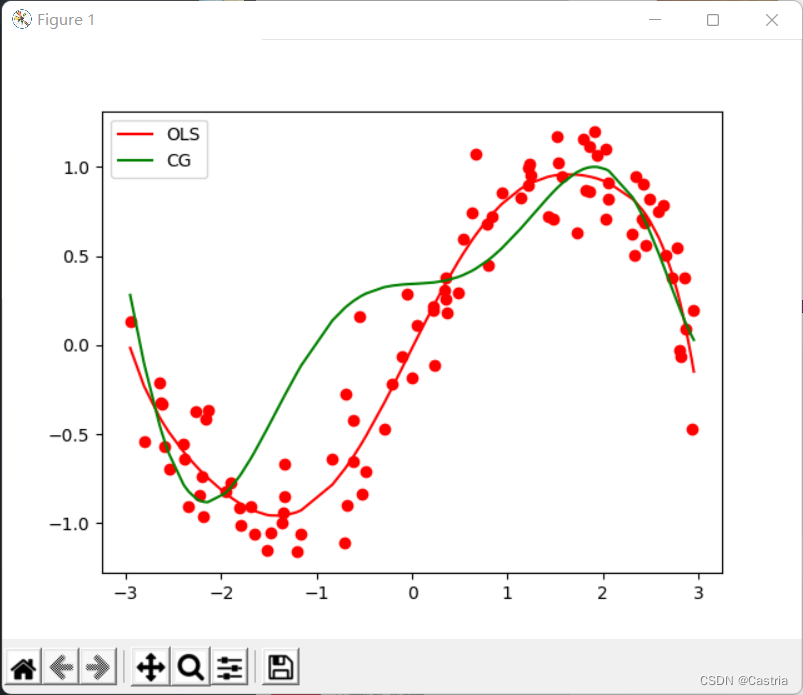
En comparación con el método de descenso de gradiente ingenuo, el método de gradiente conjugado converge de forma rápida y estable. Sin embargo, a medida que aumenta el grado del polinomio, el ajuste empeora: en $metro=7$ , se compara con el método de los mínimos cuadrados de la siguiente manera:

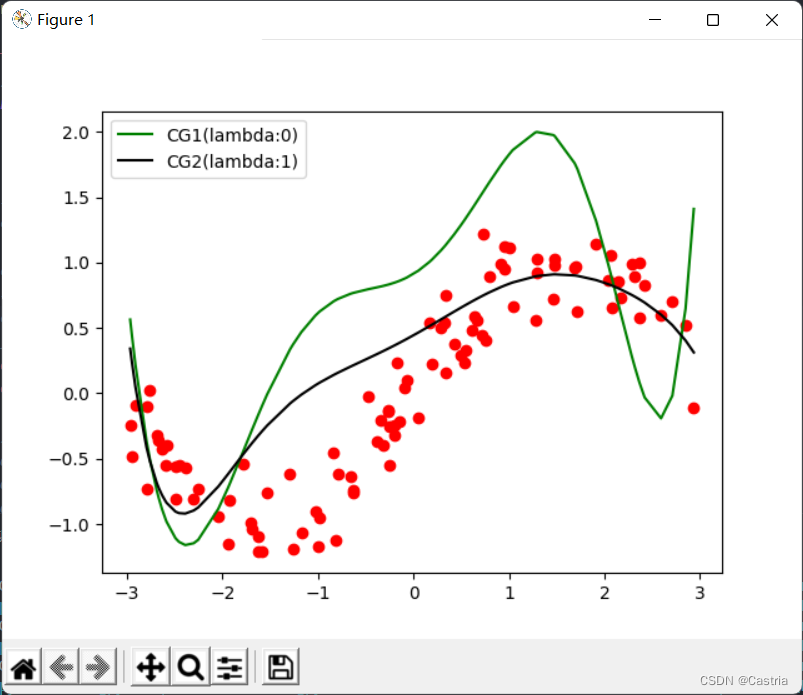
en este momento, todavía puede aliviarse parcialmente con el término regular (la cifra es$metro=7,yo=1$ ):

finalmente, se adjuntan las imágenes de ajuste de los cuatro métodos (básicamente lo mismo) y la función principal, y los parámetros se pueden ajustar de acuerdo con los requisitos experimentales:

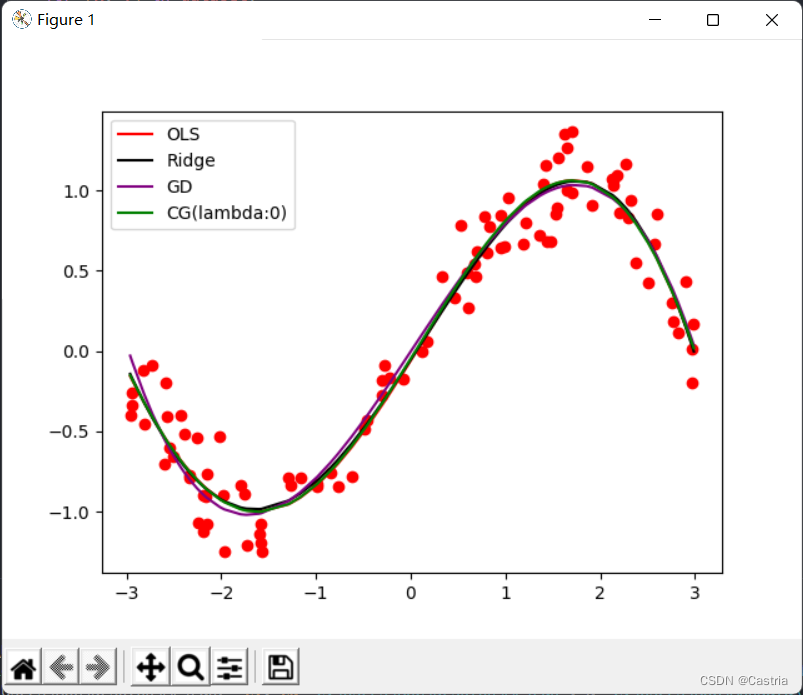
if __name__ == '__main__':
    warnings.simplefilter('error')

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    
    # 最小二乘法
    coef1 = fit(dataset)
    # 岭回归
    coef2 = ridge_regression(dataset)
    # 梯度下降法
    coef3 = GD(dataset, m = 3)
    # 共轭梯度法
    coef4 = CG(dataset)
    
    # 绘制出四种方法的曲线
    draw(dataset, coef1, color = 'red', label = 'OLS')
    draw(dataset, coef2, color = 'black', label = 'Ridge')
    draw(dataset, coef3, color = 'purple', label = 'GD')
    draw(dataset, coef4, color = 'green', label = 'CG(lambda:0)')

    # 绘制标签, 显示图像
    plt.legend()
    plt.show()