Indique la fuente de la reimpresión original de Yunzhi QMS
Autor: Wang Hongshi
1. ¿Qué es un diagrama de dispersión?
El diagrama de dispersión (Scatter Plot o Scatter Chart), también conocido como gráfico de dispersión, como su nombre lo indica, es un gráfico compuesto por algunos puntos dispersos, la posición de estos puntos está determinada por sus valores X e Y. Por lo tanto, también se le llama diagrama de dispersión XY. Muestra todos los datos en forma de puntos en el sistema de coordenadas cartesianas para mostrar el grado de interacción entre las variables, y la posición del punto está determinada por el valor de la variable.
Al analizar datos independientes, puede usar el histograma y Plato para encontrar directamente el punto de mejora, pero cuando desea analizar la correlación entre las dos variables X e Y, necesita usar el diagrama de dispersión. Como la temperatura de enfriamiento y la dureza del acero, el par y la resistencia a la tracción de los tornillos, la temperatura y la viscosidad del aceite, el contenido de plomo y la resistencia a la radiación en el vidrio, etc.
Las personas a menudo usan diagramas de dispersión para expresar la relación entre dos variables continuas X e Y. Cada punto en la figura representa cada muestra en el conjunto de datos de destino. La distribución de puntos de datos en el plano de coordenadas cartesianas y la variable dependiente varía con el El general tendencia de la variable. A partir de esta tendencia, se puede seleccionar la función adecuada para ajustarse a la distribución empírica. Al mismo tiempo, algunas líneas rectas y curvas a menudo se ajustan en el diagrama de dispersión para representar ciertos modelos y luego encontrar la relación funcional entre las variables.

2. El papel del diagrama de dispersión
Un diagrama de dispersión muestra una serie como un conjunto de puntos, con valores representados por la posición de los puntos en el gráfico y categorías representadas por distintos marcadores en el gráfico. Los diagramas de dispersión se utilizan a menudo para comparar datos agregados entre categorías. Hay muchas aplicaciones. Dos aplicaciones comunes se resumen a continuación.
2.1 Análisis de regresión
El diagrama de dispersión se utiliza en el análisis de regresión. El diagrama de distribución de puntos de datos en el plano del sistema de coordenadas cartesianas. El diagrama de dispersión indica la tendencia general de cambio de la variable dependiente con la variable independiente. Con base en esto, se puede establecer una función apropiada. seleccionados para ajustarse a los puntos de datos.
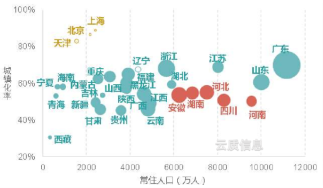
Después del análisis de regresión, el diagrama de dispersión puede predecir y analizar objetos relacionados, lo que nos permite descubrir la relación oculta entre las variables y luego tomar decisiones científicas en lugar de la ambigüedad. Por ejemplo, el siguiente diagrama de dispersión de los precios de la vivienda puede mostrarnos el aumento de los precios de la vivienda en diferentes ciudades de manera intuitiva y proporcionar un apoyo importante para los ajustes posteriores de la política de precios de la vivienda.

2.2 Análisis de correlación
El gráfico de dispersión se utiliza en el análisis de correlación. Se utilizan dos conjuntos de datos para formar múltiples puntos de coordenadas, y se examina la distribución de los puntos de coordenadas para determinar si existe una cierta relación entre las dos variables o para resumir el patrón de distribución de la puntos de coordenadas.
Al observar la distribución de puntos de datos en un diagrama de dispersión, podemos inferir correlaciones entre variables. Si no hay correlación entre las variables, el diagrama de dispersión aparecerá como puntos discretos distribuidos aleatoriamente. Si hay cierta correlación, la mayoría de los puntos de datos serán relativamente densos y estarán presentes en una tendencia determinada.
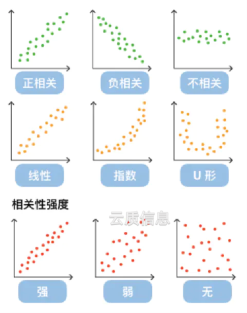
El valor central del diagrama de dispersión radica en descubrir la relación entre las variables. No entienda simplemente esta relación como una relación de regresión lineal. Hay muchas relaciones entre variables, como la relación lineal, la relación exponencial, la relación logarítmica, etc. Por supuesto, la ausencia de relación también es una relación importante.

La relación de correlación de datos se divide principalmente en: correlación positiva (los valores de dos variables aumentan al mismo tiempo), correlación negativa (el valor de una variable aumenta y el valor de la otra variable disminuye), no correlacionada, correlación lineal, correlación exponencial, etc. , que se muestran en el diagrama de dispersión. La distribución aproximada se muestra en la siguiente figura. Aquellos puntos que están lejos del grupo de puntos se denominan valores atípicos o puntos anormales.
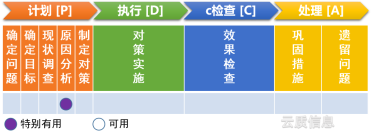
Desde la perspectiva de PDCA, la aplicación del diagrama de dispersión se resume de la siguiente manera:
3. Deformación del diagrama de dispersión
Basado en diferentes escenarios de aplicación, el gráfico de dispersión tiene muchas deformaciones, y varias deformaciones comunes se enumeran a continuación.
- Matriz de diagrama de dispersión
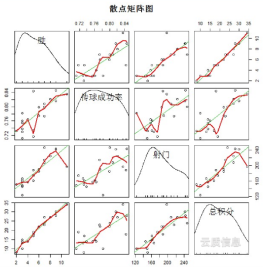
Cuando desea examinar la correlación entre múltiples variables al mismo tiempo, es muy complicado dibujar un diagrama de dispersión simple entre ellas una por una. En este momento, la matriz de diagramas de dispersión se puede usar para dibujar los diagramas de dispersión entre las respectivas variables al mismo tiempo, de modo que se pueda encontrar rápidamente la correlación principal entre múltiples variables, lo cual es especialmente importante cuando se realiza una regresión lineal múltiple. La siguiente matriz de diagrama de dispersión muestra la relación entre el total de puntos del equipo, las victorias, la tasa de pases exitosos y los tiros a puerta.
- diagrama de dispersión 3D
Aunque la relación entre múltiples variables se puede observar al mismo tiempo en la matriz del diagrama de dispersión, es posible que se pierda información importante si se realiza la observación de dos por dos del diagrama de dispersión del plano. El diagrama de dispersión tridimensional es para estudiar la relación entre las variables en el espacio tridimensional determinado por las tres variables. Dado que las tres variables se consideran al mismo tiempo, la información que no se puede encontrar en el gráfico bidimensional a menudo se puede encontró. El siguiente gráfico de dispersión tridimensional muestra la relación entre el total de puntos, las victorias y los tiros a puerta del equipo.

- gráfico de burbujas
Se puede usar un gráfico de burbujas para mostrar la relación entre tres variables. Los datos organizados en columnas en una hoja de cálculo (valores x enumerados en la primera columna, valores y correspondientes y valores de tamaño de burbuja en columnas adyacentes) se pueden trazar en un gráfico de burbujas.
Los gráficos de burbujas son similares a los gráficos de dispersión, excepto que permiten incluir una variable de tamaño adicional en el gráfico. En efecto, es como trazar un gráfico de tres variables en dos dimensiones. Las burbujas están representadas por marcadores de diferentes tamaños (que indican la importancia relativa).
4. Aplicación del diagrama de dispersión
Hay muchos beneficios de aplicar diagramas de dispersión, y los puntos comúnmente usados se resumen a continuación:
- La relación entre la causa y el resultado se puede encontrar: recopilar los datos de la causa y los datos del resultado, y compararlos.
- Dibuje un diagrama de dispersión para ver los resultados de un vistazo: En el diagrama de dispersión, los puntos de datos de causa y efecto están representados por coordenadas X e Y.
- Se puede juzgar si existe una relación o no: la relación entre los dos conjuntos de datos se puede entender claramente a partir del diagrama de dispersión.
Nota: Si los datos recopilados no se pueden juzgar en el gráfico, primero se deben separar de la capa y luego hacer clic para dibujar un gráfico de dispersión.
Los datos enumerados en la siguiente tabla son la tabla de registro de la temperatura de enfriamiento X y la dureza Y de una determinada pieza de acero recopilada. ¿Existe una correlación entre las dos variables temperatura de templado X y dureza Y?

Si solo observa los datos de la tabla anterior, ¿puede ver cuáles son las características de los datos anteriores? Definitivamente no, pero lo trazamos como un diagrama de dispersión y los datos claramente tienen una cierta tendencia.

Será más obvio si le agregamos una línea de tendencia.
