1. ¿Por qué utilizar el árbol binario de pistas?
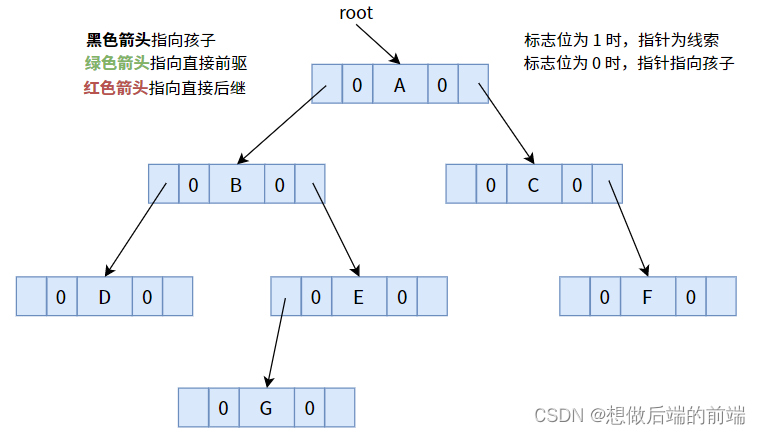
Primero veamos las deficiencias de los árboles binarios ordinarios. El siguiente es un árbol binario ordinario (método de almacenamiento encadenado):
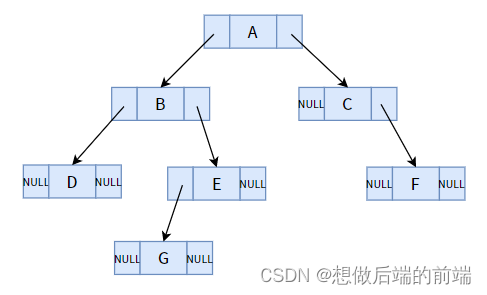
¿A primera vista parece inconsistente? Toda la estructura tiene un total de 7 nodos y un total de 14 campos de puntero, de los cuales 8 campos de puntero están vacíos. Para un árbol binario con n nodos, habrá un total de n + 1 campos de puntero nulo. Esta regla se aplica a todos los árboles binarios.
¿No parece un desperdicio tantos campos de puntero nulo? El objetivo de nuestro aprendizaje de estructuras de datos y algoritmos es encontrar formas de mejorar la eficiencia del tiempo y la utilización del espacio. Se desperdician tantos campos de puntero, ¡qué desperdicio!
Por lo tanto, tenemos que encontrar formas de hacer un buen uso de ellos y utilizarlos para ayudarnos a utilizar mejor la estructura de datos del árbol binario.
Entonces, ¿cómo aprovecharlo?
La esencia de atravesar un árbol binario es convertir los nodos de la estructura no lineal en el árbol binario en una secuencia lineal , para que podamos atravesarlo fácilmente.
Por ejemplo, la secuencia transversal en orden en la figura anterior es: DBGEACF.
Para una secuencia lineal (tabla lineal), tiene los conceptos de predecesor directo y sucesor directo. Por ejemplo, en una secuencia transversal en orden, el predecesor directo de B es D y el sucesor directo es G.
La razón por la que podemos conocer el predecesor directo y el sucesor directo de B es porque escribimos la secuencia transversal en orden del árbol binario de acuerdo con el algoritmo transversal en orden, y luego usamos esta secuencia para saber de quién es el predecesor y el sucesor. OMS.
El predecesor directo y el sucesor directo no se pueden obtener directamente a través del árbol binario, porque solo existe una relación directa entre los nodos padres e hijos en el árbol binario, es decir, el campo de puntero de nodo del árbol binario solo almacena la dirección de su nodo hijo.
El requisito actual es que quiero poder obtener directamente el predecesor directo y el sucesor directo de un nodo en modo transversal en orden del árbol binario.
En este momento, es necesario utilizar el árbol binario de pistas.
2. ¿Qué es un árbol binario de pistas?
Por supuesto, definitivamente necesitamos usar el campo de puntero del nodo para guardar las direcciones del predecesor inmediato y del sucesor inmediato.
De hecho, en el árbol binario ordinario de la figura anterior (la secuencia obtenida atravesando en orden intermedio), algunos nodos (nodos cuyos campos de puntero no están vacíos) pueden encontrar sus predecesores o sucesores directos, como el hijo izquierdo G del nodo E es el predecesor directo del nodo E; el hijo derecho C del nodo A es el sucesor directo del nodo A.
Pero no funciona para algunos nodos (el campo del puntero está vacío), por ejemplo, el sucesor directo del nodo G es E y el predecesor directo es B. Sin embargo, tal conclusión no se puede sacar en un árbol binario. ¿Cómo hacerlo? Notamos que los dos campos de puntero del nodo G son NULL y no se han utilizado, entonces, ¿no sería bueno si usáramos estos dos punteros para señalar a su predecesor y sucesor respectivamente?
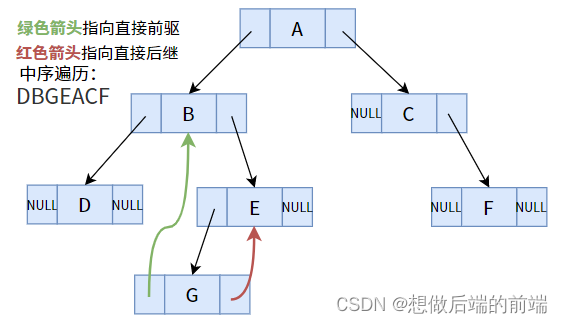
Es realmente lo mejor de ambos mundos, ¡una combinación perfecta! ¡Pero el problema no está resuelto!
Debido a que usamos el campo de puntero nulo para señalar al predecesor o sucesor, esto es contradictorio para aquellos nodos cuyo campo de puntero no está vacío, como el nodo E y el nodo B.
Dado que hay un conflicto, debemos descubrir la causa raíz del conflicto y resolverla.
La fuente de la contradicción es: cuando el campo del puntero del nodo está vacío y no vacío, el puntero del puntero es inconsistente. Es decir, existe una contradicción entre el puntero que apunta al hijo cuando no está vacío y el predecesor o sucesor cuando el puntero está vacío.
Luego tomamos el medicamento correcto, distinguimos el campo del puntero que está vacío y el que no, y le decimos claramente al puntero: cuando no está vacío, apunta al niño, y cuando está vacío, apunta al predecesor o sucesor. Esto requiere que agreguemos un bit de bandera a cada uno de los dos punteros.
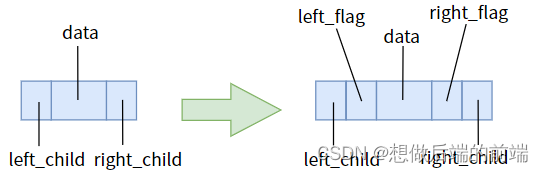
Y acuerde las siguientes reglas:
Cuando left_flag == 0, el puntero left_child apunta al hijo izquierdo
. Cuando left_flag == 1, el puntero left_child apunta al predecesor inmediato.
Cuando right_flag == 0, el puntero right_child apunta a la derecha niño
Cuando right_flag == 1, el puntero right_child apunta al predecesor inmediato.
Los nodos del árbol binario deben cambiar:
/*线索二叉树的结点的结构体*/
typedef struct Node {
char data; //数据域
struct Node *left_child; //左指针域
int left_flag; //左指针标志位
struct Node *right_child; //右指针域
int right_flag; //右指针标志位
} TTreeNode;
Con el bit de bandera se puede solucionar todo. Llamamos pistas a los indicadores de predecesores y sucesores inmediatos. Un puntero con una bandera de 0 es un puntero a un niño y un puntero con una bandera de 1 es una pista.
Un árbol de lista enlazada binaria tiene la estructura de nodos como se muestra arriba. Convertimos todos los punteros nulos en pistas. Un árbol binario de este tipo es un árbol de pistas binarias.
3. ¿Cómo crear un árbol binario de pistas?
En un árbol binario ordinario, si queremos obtener el predecesor o sucesor directo de un nodo en un determinado orden transversal, debemos recorrer para obtener el orden transversal cada vez antes de que podamos conocerlo. En el árbol binario de pistas, solo necesitamos atravesarlo una vez (recorrido al crear el árbol binario de pistas), después de eso, el árbol binario de pistas puede "recordar" el predecesor y sucesor directo de cada nodo, y no es necesario obtenerlo. a través del orden transversal en el futuro Precursor o sucesor.
El proceso en el que transformamos un árbol binario ordinario en un árbol binario con pistas de acuerdo con un determinado método transversal se llama subprocesamiento de un árbol binario.
A continuación, utilizamos el recorrido en orden para convertir la siguiente pista del árbol binario en un árbol binario de pistas.
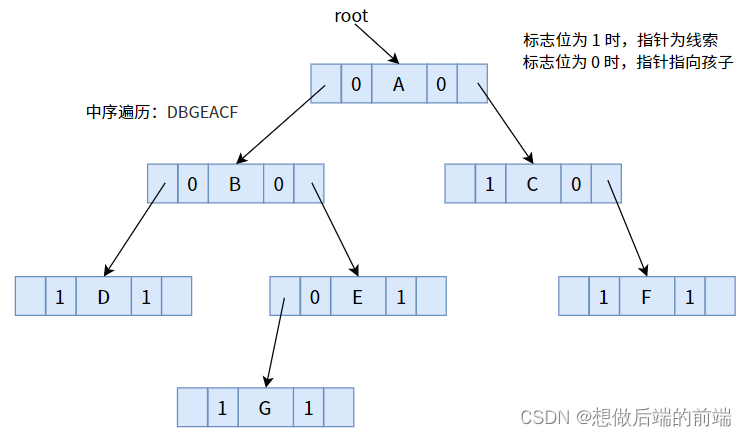
Utilice el puntero con el bit de bandera 1 para recorrer la secuencia en orden para que apunte al predecesor o sucesor:
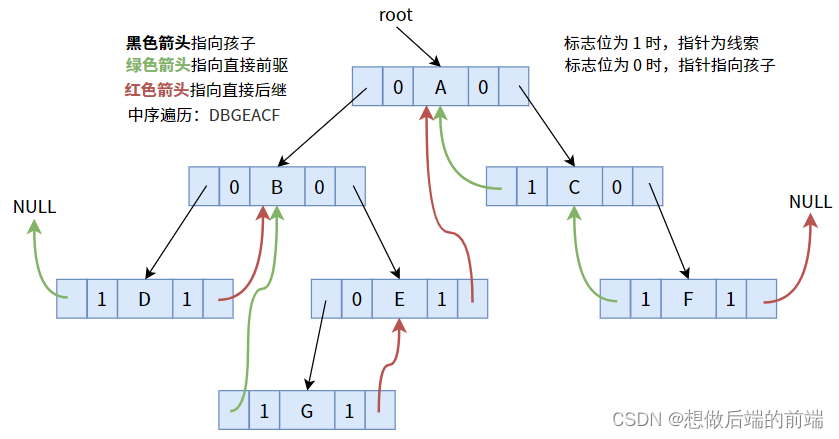
entre ellos , el nodo D no tiene un predecesor directo y el nodo F no tiene un sucesor directo, por lo que el puntero es NULL.
En este punto, hemos resuelto el desperdicio causado por n + 1 campos de puntero nulo en un árbol binario con n nodos. La solución es agregar un bit de bandera al puntero de cada nodo para hacer uso del campo de puntero nulo. El bit de bandera almacena un valor booleano de 0 o 1, que es relativamente rentable en comparación con el campo de puntero nulo desperdiciado. Además, el árbol binario tiene una nueva característica: las relaciones predecesoras y sucesoras entre nodos en un determinado orden transversal se pueden guardar en el árbol binario.
4. Realización de pistas
Tenga en cuenta que el árbol binario de pistas se obtiene del árbol binario ordinario y se obtiene en un determinado orden transversal. Debido a que solo se pueden establecer pistas después de conocer el predecesor y el sucesor de un nodo, y la relación entre el predecesor y el sucesor no se puede reflejar directamente a través del árbol binario, la relación solo se puede obtener a través de la secuencia lineal obtenida al atravesar el árbol binario. Por lo tanto, después de obtener la secuencia con la relación predecesora y sucesora mediante algún tipo de método transversal, se puede modificar el puntero nulo del nodo y luego se puede establecer la pista.
Es decir: la esencia del subproceso es el proceso de modificar el puntero nulo de un nodo durante el proceso de atravesar un árbol binario en un determinado orden transversal para que apunte a su predecesor inmediato o sucesor directo en ese orden transversal.
Entonces, la estructura general del código sigue siendo la misma, solo necesitamos reemplazar el código de impresión en el código transversal con el código de subproceso y realizar algunos otros cambios.
La siguiente figura es un ejemplo para introducir tres tipos de pistas:
Un árbol binario sin subprocesos tiene todos los indicadores por defecto en 0.
4.1 Roscado entre secuencias
Después de realizar una pista de acuerdo con el orden transversal, se puede obtener la siguiente figura:
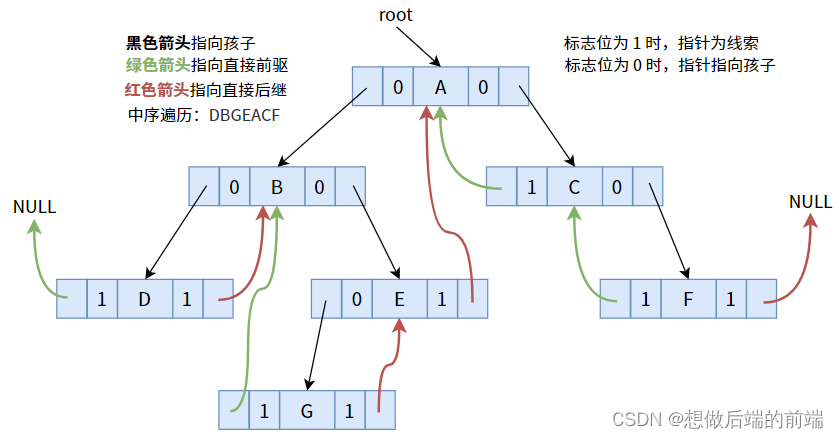
Primero aclaremos nuevamente el siguiente contenido:
- Realizamos subprocesos mientras atravesamos el árbol binario.
- El orden del recorrido en orden es: subárbol izquierdo >> raíz >> subárbol derecho.
- El subprocesamiento modifica dos cosas: el campo del puntero nulo y su correspondiente bit de bandera.
- ¿Cómo modificar? Establece el campo de puntero nulo al predecesor o sucesor inmediato.
Entonces nuestra pregunta es:
- Encuentra todos los campos de puntero nulo.
- Encuentre el nodo al que pertenece el campo de puntero nulo, el predecesor directo y el sucesor directo en orden de reserva.
- Modifique el contenido del campo del puntero nulo y su bandera para que el puntero se llame pista.
Nota: Usamos recursividad al atravesar el árbol binario, por lo que también la usaremos al enhebrar.
El código específico es el siguiente:
//全局变量 prev 指针,指向刚访问过的结点
TTreeNode *prev = NULL;
/**
* 中序线索化
*/
void inorder_threading(TTreeNode *root)
{
if (root == NULL) {
//若二叉树为空,做空操作
return;
}
inorder_threading(root->left_child);
if (root->left_child == NULL) {
root->left_flag = 1;
root->left_child = prev;
}
if (prev != NULL && prev->right_child == NULL) {
prev->right_flag = 1;
prev->right_child = root;
}
prev = root;
inorder_threading(root->right_child);
}
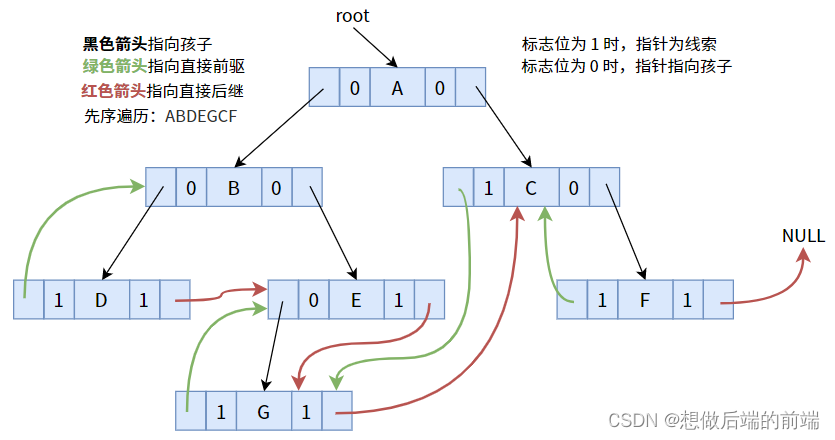
4.2. Enhebrado de pedidos anticipados
Después de seguir la secuencia de pedido anticipado, se puede obtener la siguiente imagen:
El código específico es el siguiente:
// 全局变量 prev 指针,指向刚访问过的结点
TTreeNode *prev = NULL;
/**
* 先序线索化
*/
void preorder_threading(TTreeNode *root)
{
if (root == NULL) {
return;
}
if (root->left_child == NULL) {
root->left_flag = 1;
root->left_child = prev;
}
if (prev != NULL && prev->right_child == NULL) {
prev->right_flag = 1;
prev->right_child = root;
}
prev = root;
if (root->left_flag == 0) {
preorder_threading(root->left_child);
}
if (root->right_flag == 0) {
preorder_threading(root->right_child);
}
}
4.3 Enhebrado posterior al pedido
Después de realizar una pista de acuerdo con el orden transversal posterior al pedido, se puede obtener la siguiente figura:
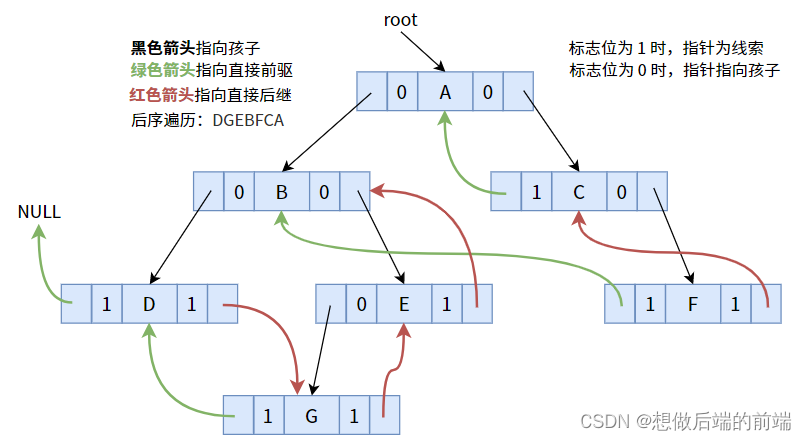
El código específico es el siguiente:
//全局变量 prev 指针,指向刚访问过的结点
TTreeNode *prev = NULL;
/**
* 后序线索化
*/
void postorder_threading(TTreeNode *root)
{
if (root == NULL) {
return;
}
postorder_threading(root->left_child);
postorder_threading(root->right_child);
if (root->left_child == NULL) {
root->left_flag = 1;
root->left_child = prev;
}
if (prev != NULL && prev->right_child == NULL) {
prev->right_flag = 1;
prev->right_child = root;
}
prev = root;
}
5. Resumen
El árbol binario subproceso hace un uso completo del campo de puntero nulo en el árbol binario y le da al árbol binario una nueva característica: después de pasar un recorrido, las relaciones predecesoras y sucesoras entre sus nodos se pueden guardar en el árbol binario.
Por lo tanto, si necesitamos recorrer con frecuencia el árbol binario para encontrar el nodo predecesor o sucesor directo de un nodo, es muy apropiado utilizar el árbol binario de pistas.