Autor: Yu Fan
fondo
Los sistemas complejos de espacio-tiempo modelados mediante ecuaciones diferenciales parciales son omnipresentes en muchas disciplinas, como las matemáticas aplicadas, la física, la biología, la química y la ingeniería. En la mayoría de los casos, no podemos obtener soluciones analíticas de las PDE utilizadas para describir estos sistemas físicos complejos, por lo que se han estudiado ampliamente los métodos de solución numérica, que incluyen: elementos finitos, diferencias finitas, análisis isogeométrico (IGA) y otros métodos. Aunque estos métodos numéricos tradicionales pueden aproximarse a la solución exacta de la ecuación mediante funciones básicas, todavía existe una enorme sobrecarga computacional en la asimilación de datos y la resolución del problema inverso.
En los últimos años, han surgido en una corriente interminable varios métodos de aprendizaje profundo para resolver problemas directos e inversos de sistemas no lineales. La investigación sobre el uso de DNN para modelar sistemas físicos se puede dividir aproximadamente en las dos categorías siguientes: redes continuas y redes discretas. Un representante típico de las redes continuas son los PINN: el residual de PDE se usa como una restricción suave de la red neuronal y se usa una capa completamente conectada para aproximar la solución de la ecuación, y el modelo se puede realizar en una escala de datos pequeña o incluso datos muestreados sin etiquetar. No obstante, los PINN a menudo se limitan a parametrizaciones de baja dimensión y se estiran cuando se enfrentan a sistemas PDE con gradientes pronunciados y morfologías locales complejas. Recientemente, una pequeña cantidad de estudios piloto han descubierto que las redes discretas tienen una mejor escalabilidad y una velocidad de convergencia más rápida que el aprendizaje continuo. Por ejemplo, CNN se puede utilizar como modelo proxy en el dominio rectangular para sistemas independientes del tiempo; Para resolver geométricamente adaptativamente ecuaciones diferenciales parciales de estado estacionario a través de la transformación de coordenadas, para sistemas dependientes del tiempo, la mayoría de los métodos de solución de redes neuronales todavía se basan en datos y en malla.
PhyCRNet[1], propuesto por el equipo del profesor Sun Hao en la Escuela de Inteligencia Artificial Hillhouse de la Universidad Renmin de China, en colaboración con la Universidad Northeastern (EE.UU.) y la Universidad de Notre Dame, es un método no supervisado para resolver PDE en dominios espaciotemporales multidimensionales. a través del conocimiento físico previo y la arquitectura de red recursiva convolucional, que combina ConvLSTM (extracción de características espaciales de baja dimensión y aprendizaje de la evolución del tiempo), conexión residual global (mapeo estricto de cambios en las soluciones de ecuaciones en el eje del tiempo) y diferencias finitas de alto orden. El filtrado espaciotemporal (que determina la construcción de una función de pérdida residual y la capacidad de las derivadas de PDE requeridas) lo convierte en una solución básica cuando se enfrentan problemas inversos y cuando hay datos escasos y ruidosos.
1. Definición del problema
Considerando ecuaciones diferenciales parciales paramétricas no lineales multidimensionales, la forma general es la siguiente:
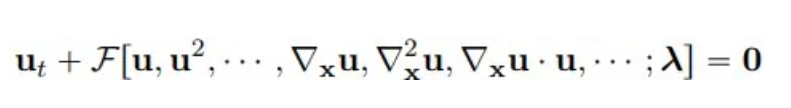
donde u(x, t) representa la solución de la ecuación en el dominio del tiempo T y el dominio del espacio Ω, y F es un funcional no lineal con parámetro λ.
**2. ** Método modelo
ConvLSTM
ConvLSTM es un marco de aprendizaje espaciotemporal de secuencia a secuencia que se extiende desde LSTM y su variante de arquitectura de predicción codificador-decodificador LSTM (que tiene la ventaja de modelar dependencias de períodos largos que evolucionan con el tiempo). En esencia, la unidad de memoria se actualiza con la información de entrada y de estado a la que se accede, y la acumulación y el borrado de la memoria se completa a través de puertas de control inteligentemente diseñadas. Con base en esta configuración, se alivia el problema de desaparición de gradiente de las redes neuronales recurrentes ordinarias (RNN). ConvLSTM hereda la estructura básica de LSTM (es decir, unidades celulares y puertas) para controlar el flujo de información y modifica la red neuronal completamente conectada (FC-NN) para tener en cuenta que CNN tiene mejores capacidades de representación de conexión espacial y realiza operaciones de puerta en CNN. . Como tipo especial de RNN, LSTM se puede utilizar como método numérico implícito para resolver ecuaciones PDE dependientes del tiempo. El diagrama de estructura de una única unidad ConvLSTM es el siguiente:
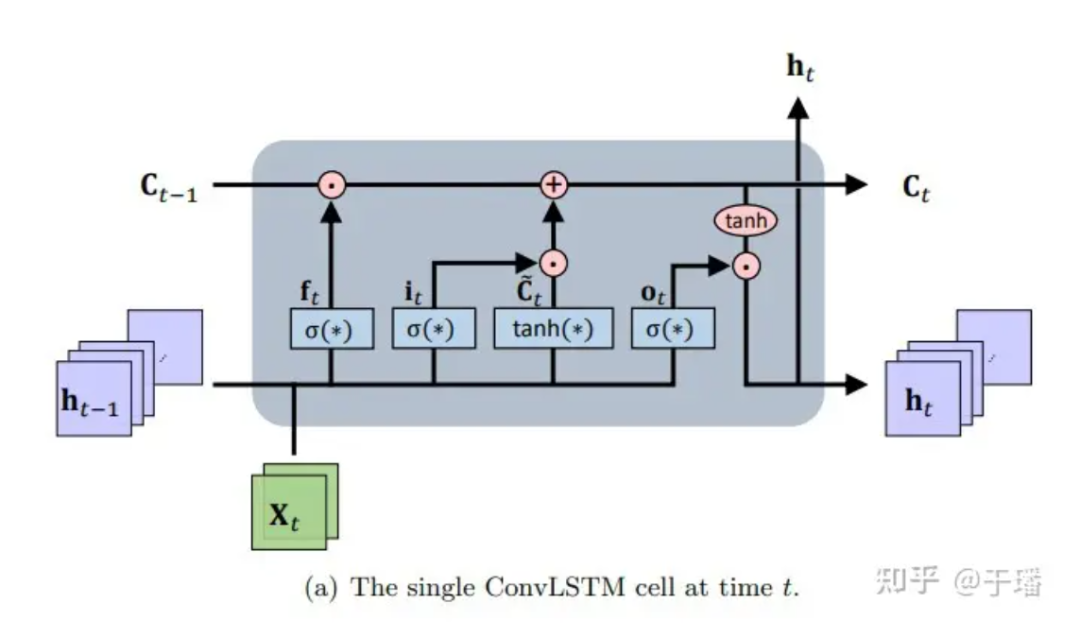Figura 1: Celda ConvLSTM única en el momento t
La representación matemática de la actualización de una unidad ConvLSTM es la siguiente:
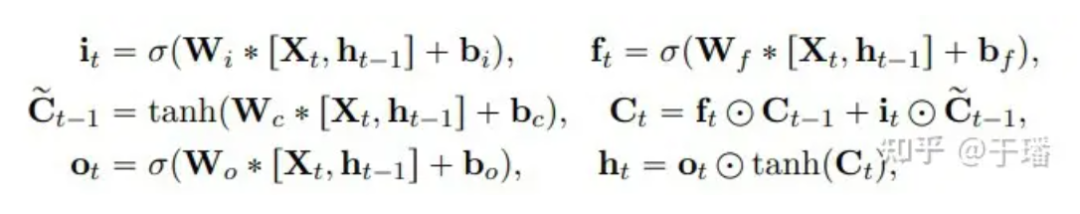
Entre ellos, * representa la operación de convolución, ⊙ representa el producto de Hadamard; W es el parámetro de peso del filtro y b representa el vector de polarización.
Mezcla de píxeles
Pixel Shuffle es una operación eficiente de convolución de subpíxeles que muestra una imagen de baja resolución (LR) a una imagen de alta resolución (HR). Supongamos que las dimensiones de un tensor de características LR son (C Un tensor HR con dimensiones (C, H xr, W xr).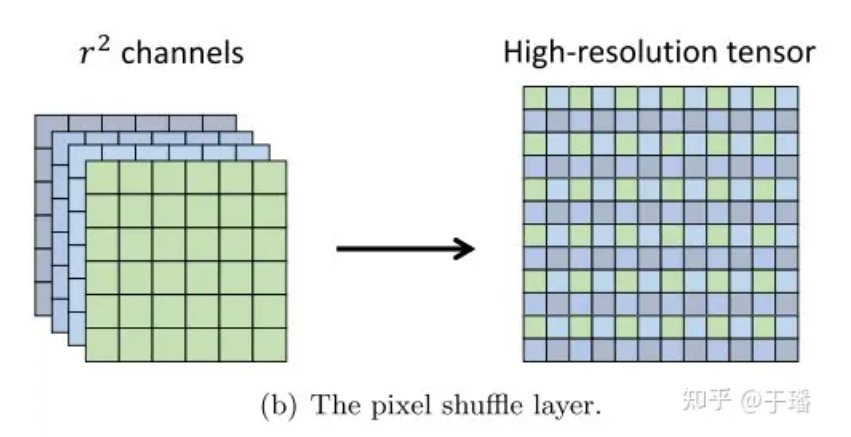 
Figura 2: capa Pixel Shuffle
La eficiencia de Pixel Shuffle se refleja en: (1) aumentar solo la resolución en la última capa de convolución, lo que puede evitar la necesidad de usar más capas de convolución para aumentar la imagen a la resolución objetivo, como la deconvolución (2); Todas las capas de extracción de características antes de la capa de muestreo ascendente, se pueden usar filtros más pequeños para procesar estos tensores de baja resolución.
PhyCRNet
PhyCRNet consta de módulos codificadores-decodificadores, conexiones residuales, procesos autorregresivos y un método diferencial basado en filtros. El codificador contiene tres capas convolucionales para aprender características latentes de baja dimensión de la variable de estado Ui en un momento determinado y dejar que evolucione con el tiempo a través de ConvLSTM. Dado que la transformación se realiza en variables de baja dimensión, la sobrecarga de memoria se reducirá en consecuencia. Además, inspirados en el método directo de Euler, podemos agregar una conexión residual global entre la variable de entrada Ui y la variable de salida Ui+1, y el proceso de aprendizaje de un solo paso se puede expresar como Ui+1 = Ui + δt x N [Ui; θ], donde N[·] representa el operador de red neuronal entrenado y δt es el intervalo de tiempo unitario. Por tanto, esta relación recursiva puede verse como un proceso autorregresivo simple.
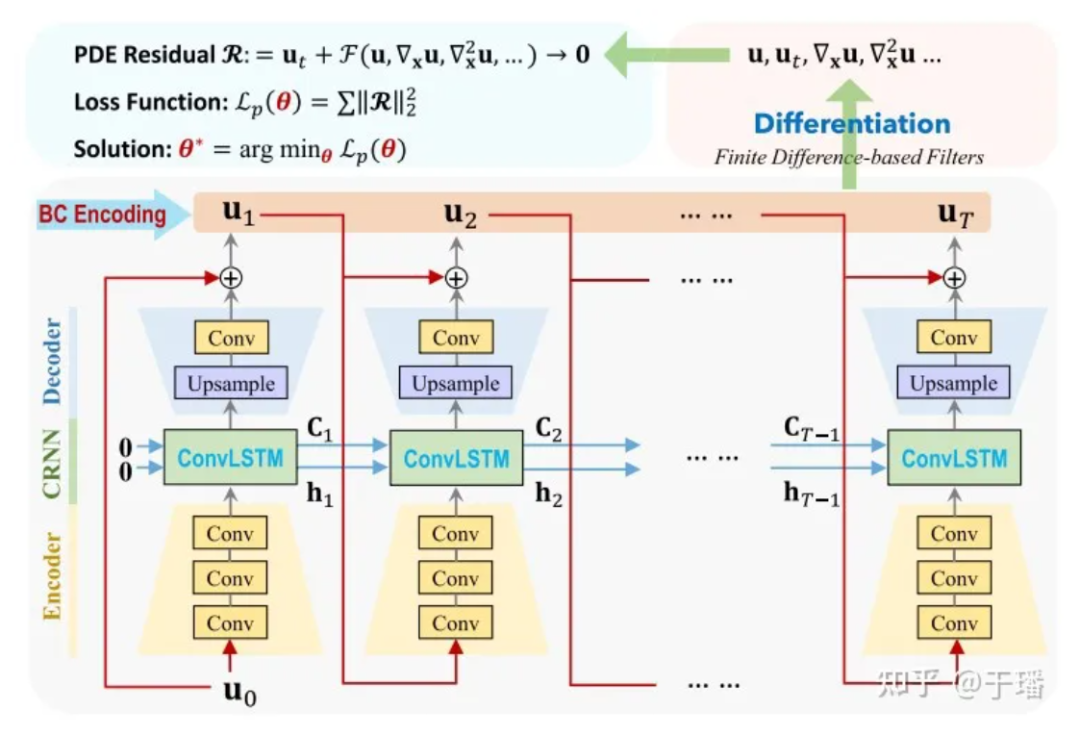Figura 3: Diagrama de estructura de la red PhyCRNet
Aquí U0 es la condición inicial, U1 a UT son las soluciones discretas que el modelo debe predecir y la evolución del tiempo desde la entrada hasta la salida. En comparación con los métodos numéricos tradicionales, ConvLSTM puede utilizar un intervalo de tiempo mayor. Para el cálculo de cada término diferencial, utilizamos un núcleo de convolución fijo [1] para representar sus valores de diferencia. En PhyCRNet, los términos de diferencia de segundo y cuarto orden se utilizan para calcular las derivadas de U con respecto al tiempo y el espacio. Para optimizar aún más el rendimiento informático, podemos omitir la parte del codificador en un ciclo de tamaño T, excepto el primer momento de cada ciclo. El diagrama esquemático es el siguiente:
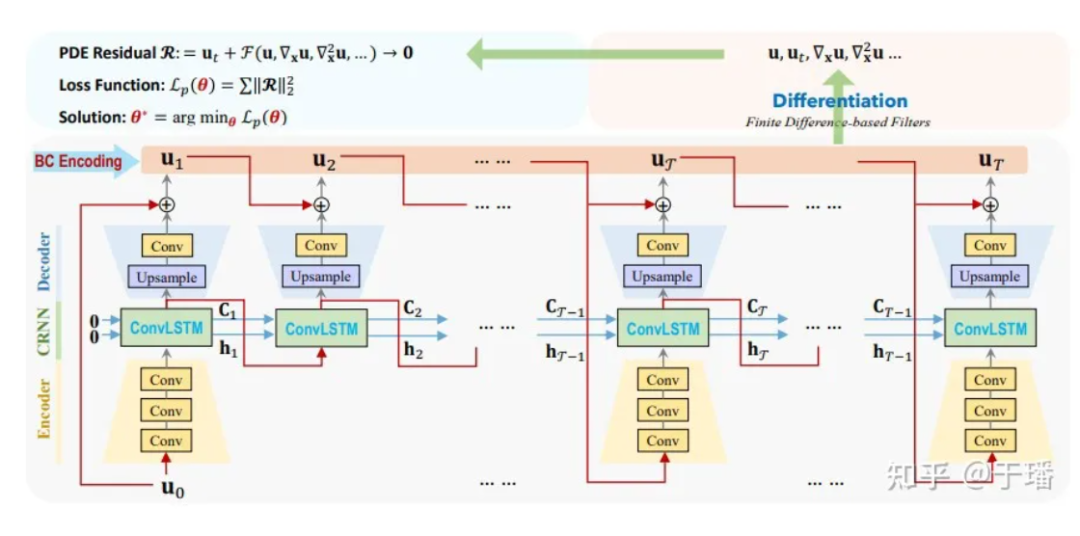Figura 4: Diagrama de estructura de red de PhyCRNet
Restricciones estrictas I/BC
En comparación con el método PINN, que utiliza condiciones de contorno iniciales físicas como restricciones suaves (sus residuos se optimizan como parte de Loss), PhyCRNet utiliza el método de codificación I/BC en el modelo (las condiciones iniciales se utilizan como entrada U0 de ConvLSTM, y las condiciones de contorno se codifican mediante relleno), de modo que las condiciones físicas ya no sean una restricción suave, mejorando así la precisión y la velocidad de convergencia del modelo. Para Dirichlet BC, los valores de límite constantes conocidos se pueden llenar directamente como relleno en el dominio espacial, mientras que para Neumann BC, se puede agregar una capa de elementos fantasma alrededor del dominio espacial, sus valores son. aproximado por diferencias durante el proceso de entrenamiento.
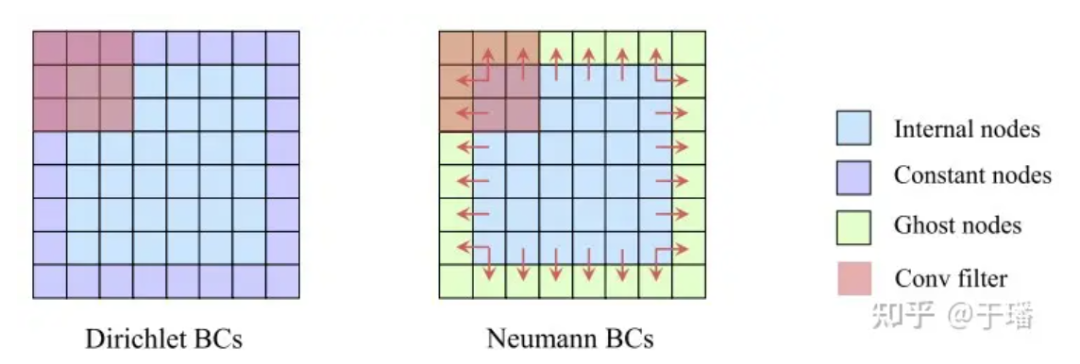Figura 5: Ilustración de restricciones estrictas en condiciones de contorno
función de pérdida
Dado que I/BC ha sido restringido rígidamente en el modelo, la función de pérdida solo necesita incluir el término residual de la PDE. Tomando como ejemplo un sistema PDE bidimensional, la función de pérdida se puede expresar como:
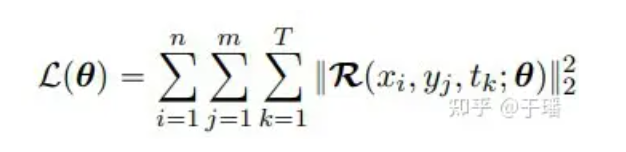
donde n y m representan la altura y el ancho de la cuadrícula, T es el número total de pasos de tiempo y R (x, t; θ) es el residual de PDE:
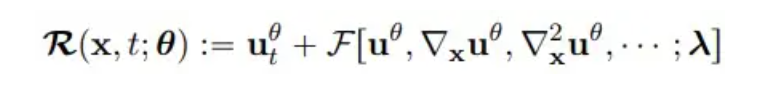
**3. ** Análisis de resultados
Para evaluar el error del modelo en todo el dominio, el error cuadrático medio acumulado (a-RMSE) en el momento τ se calcula de la siguiente manera:
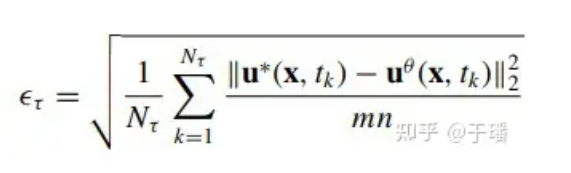
donde Nτ es el número de pasos de tiempo en [0, τ] y u*(x, t) es la solución de referencia de la ecuación.
Ecuación de hamburguesas bidimensional
Considere un problema clásico en mecánica de fluidos, dada la ecuación de Burgers bidimensional de la siguiente forma:
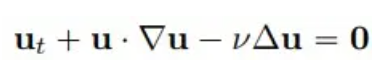
Seleccionamos 4 puntos de tiempo: entrenamiento (t = 1.0, 2.0) y extrapolación (t = 3.0, 4.0) para comparar la precisión de la solución y las capacidades de extrapolación de los métodos PhyCRNet y PINN:
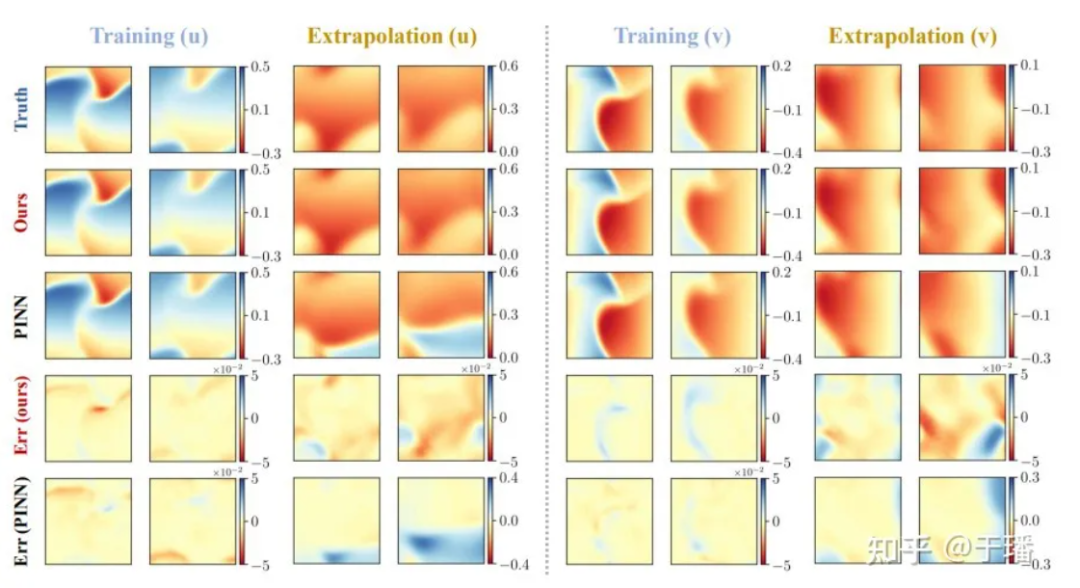Figura 6: Resultados de entrenamiento y extrapolación de PhyCRNet versus PINN para la ecuación bidimensional de Burgers
Ecuación λ-ω RD
Como segundo caso, considere un sistema bidimensional λ-ω RD (usado a menudo para representar procesos bioquímicos de múltiples escalas):
Entre ellos, u y v son dos variables de campo que satisfacen:
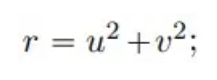
λ y ω son dos funciones de valor real:
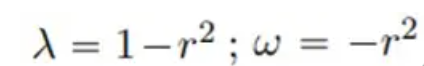
La solución de referencia para un total de 801 pasos de tiempo en el área [-10, 10] se genera mediante el método espectral después del entrenamiento para 200 pasos de tiempo en el período de tiempo [0, 5], la solución de referencia para [5, 10]; ] La predicción se realiza durante el período y los resultados de la predicción que comparan PhyCRNet y PINN son los siguientes:
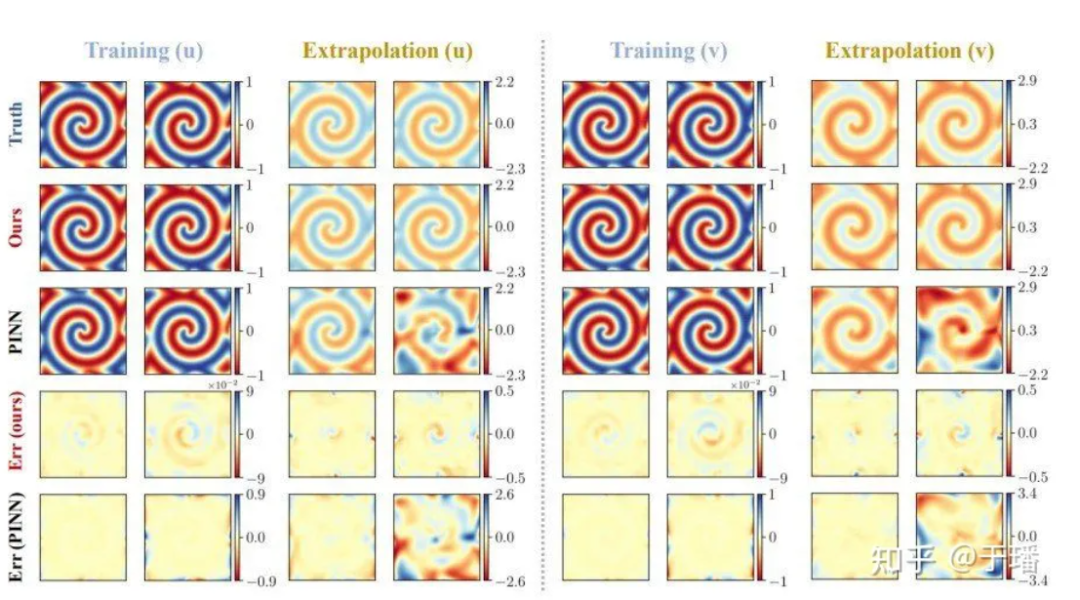Figura 7: Resultados de extrapolación y entrenamiento de PhyCRNet versus PINN para la ecuación λ-ω RD
La siguiente figura muestra las curvas de propagación de errores de PhyCRNet y PINN durante el entrenamiento y la extrapolación en los dos sistemas PDE mencionados anteriormente. Se puede ver claramente que PhyCRNet funciona mejor en ambas etapas (especialmente en la etapa de extrapolación).
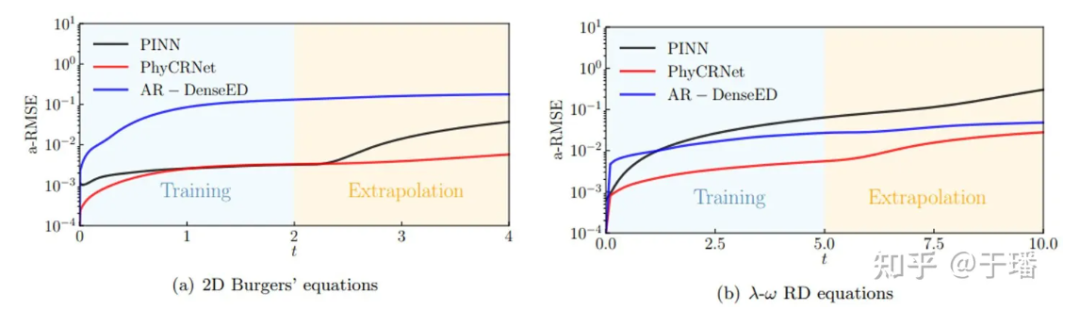Figura 8: Comparación de la propagación de errores de PhyCRNet y PINN
referencias
[1] Ren P, Rao C, Liu Y, et al. PhyCRNet: red convolucional recurrente basada en la física para resolver PDE espaciotemporales [J]. Métodos informáticos en ingeniería y mecánica aplicada, 2022, 389: 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
Un programador nacido en los años 90 desarrolló un software de portabilidad de vídeo y ganó más de 7 millones en menos de un año. ¡El final fue muy duro! Google confirmó despidos, relacionados con la "maldición de 35 años" de los codificadores chinos en los equipos Python Flutter Arc Browser para Windows 1.0 en 3 meses oficialmente GA La participación de mercado de Windows 10 alcanza el 70%, Windows 11 GitHub continúa disminuyendo. GitHub lanza la herramienta de desarrollo nativo de IA GitHub Copilot Workspace JAVA. es la única consulta de tipo fuerte que puede manejar OLTP + OLAP. Este es el mejor ORM. Nos encontramos demasiado tarde.