table des matières
Algorithme euclidien (algorithme euclidien)
L'algorithme euclidien est également appelé méthode de lancer et de division, qui est principalement utilisée pour calculer le plus grand diviseur commun de deux entiers a et b.
Parlez simplement du principe de l'algorithme: le plus grand diviseur commun de deux entiers est égal au plus grand diviseur commun du plus petit et le plus grand divisé par le petit reste.
Soit: pgcd (a, b) = pgcd (b, a mod b).
Donnez un exemple simple: par
exemple, trouvez le plus grand diviseur commun a = pgcd (10, 24) de 10 et 24:
- Trouver le plus grand diviseur commun de 10 et 24 équivaut à trouver le plus grand diviseur commun de 10 et 4:
a = pgcd (10, 24) = pgcd (10, 4) - Trouver le plus grand diviseur commun de 10 et 4 équivaut à trouver le plus grand diviseur commun de 4 et 2, qui est 2:
a = pgcd (10, 24) = pgcd (10, 4) = pgcd (4, 2) = 2
# python
def gcd(a, b):
return a if b == 0 else gcd(b, a % b)
print(gcd(10,24)) # 2
Algorithme euclidien étendu
Principe de l'algorithme: Si a et b sont des entiers positifs, il existe des entiers x, y tels que gcd (a, b) = ax + by; en
termes simples, gcd (a, b) peut être exprimé comme une combinaison linéaire d'entiers de a et b.
Donnez un exemple simple:
gcd (10, 24) = 2
2 = 10 * (- 7) + 24 * 3
Les principales applications sont les suivantes:
-
Résoudre l'équation indéterminée;
exemple: trouver un ensemble de solutions entières de 435x + 783y = 87:Commencez par parcourir l'algorithme d'Euclid:
783 = 1× 435 + 348 435 = 348×1 + 87 348 = 87 × 4 + 0 ∴ 87 = 435 – 348 87 = 435 – (783 – 435) 87 = (–1)(783) + 2(435) ∴ x = 2, y = −1是此不定方程的一组整数解。 -
Résoudre l'élément inverse du module (élément inverse multiplicatif), se référer à l'article précédent sur les équations de congruence, les fonctions d'Euler, les éléments inverses multiplicatifs et l'inversion de matrice définie sur Zm ;
-
Résoudre des équations linéaires modulaires (équations de congruence linéaire);
-
Résoudre l'équation de congruence ax ≡ b (mod m), x =?
Prenons un exemple extrêmement représentatif: 15x = 1 mod 26 Ce
problème est transformé en 15x-26y = 1 peut être utilisé comme 1 pour résoudre l'équation indéfinie, ou comme 2 Trouvez l'inverse multiplicatif解法如下: 26 = 1× 15 + 11 15 = 11×1 + 4 11 = 4 × 2 + 3 4 = 1 × 3 + 1 3 = 1 × 3 ∴ 1 = 4 – 3 = 4 – (11 – 4×2) = 4×3 – 11 = (15-11) ×3 - 11 = 15×3 - 11×4 = (26-11)×3 - 11 ×4 = 26×3 - (26 - 15)×7 =26×(-4) + 15×7 ∴ x = 7, y = −4 为此不定方程的一组整数解,15关于模26的乘法逆元为7 -
Résolvez le système d'équations de congruence et continuez à regarder le théorème du reste chinois
-
Théorème du reste chinois
Il y a une question dans "Sun Tzu Suan Jing": "Aujourd'hui, il y a des choses qui ne connaissent pas le nombre, deux des trois ou trois sont laissées (divisez par 3 et restent 2), et
trois des cinq et cinq sont laissées (divisez par 5 et restez 3), sept ou sept. Deux des nombres restants (divisez par 7 restent 2), quel est le problème? "
Le mathématicien de la dynastie Song Qin Jiushao a fait une réponse complète et systématique au problème des «choses ne connaissent pas le nombre» dans les volumes 1 et 2 de «Neuf chapitres de mathématiques» en 1247. Le mathématicien de la dynastie Ming Cheng Dawei a compilé la solution dans le "Sun Tzu Ge Jue" facile à utiliser:
三人同行七十稀,
五树梅花廿一支,
七子团圆正半月,
除百零五便得知。
Cela signifie que tant qu'il reste un 1 après la division par 3, un 70 est ajouté;
tant qu'il reste un 1 après la division par 5, un 21 est ajouté;
tant qu'il reste un 1 après la division par 7, un 15 est ajouté. Puis additionnez.
Enfin, calculez le reste de cette somme divisé par 105.
Soit (2 × 70 + 3 × 21 + 15 × 2) mod 105 = 23
La solution est la suivante:
Découvrez d'abord les plus petits nombres 15, 21, 70 qui sont divisés par 7, 5 et 3 des multiples communs de 3 et 5, 3 et 7, 5 et 7, respectivement (cette étape est également appelée "modulo inverse" " Opération, reportez-vous à la solution d'élément inverse de multiplication). Soit:
15 ÷ 7 = 2 …… Restant 1,
21 ÷ 5 = 4 …… Restant 1,
70 ÷ 3 = 23 …… Restant 1.
Utilisez ensuite les trois plus petits nombres trouvés pour multiplier le nombre requis par 7. Le produit du reste obtenu en divisant, 5 et 3 est ajouté en continu,
15 × 2 + 21 × 3 + 70 × 2 = 233.
Enfin, divisez 233 par le plus petit commun multiple des trois diviseurs de 3, 5 et 7.
233 ÷ 105 = 2 ...... Le reste est 23,
ce reste 23 est le plus petit nombre qui remplit les conditions.
Étendre à la situation générale: en
supposant que les entiers m1, m2,…, mn sont mutuellement premiers, alors pour tout entier: a1, a2,…, un système d'équations:
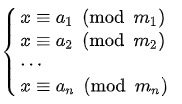
il existe des solutions entières, et si X, Y satisfont le système d'équations , Il doit y avoir X ≡ Y (mod N) où: La
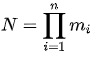
formule est la suivante:
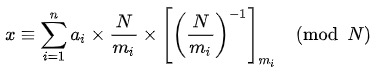
Je ne veux vraiment pas regarder les symboles de formule dans le manuel. Prenons les devoirs et donnons deux exemples.
Devoir 1:
Résoudre le système d'équations de congruence:
x ≡ 12 (mod 25)
x ≡ 9 (mod 26)
x ≡ 23 (mod 27)
Les équations ci-dessus sont équivalentes à x = 25a + 12 = 26b + 9 = 27c + 23.
Décalez les termes pour obtenir:
①: 25a-27c = 23-12 = 11
②: 26b-25a = 12-9 = 3
Tout d'abord, utilisez Euclidean pour développer Euclidean:
27 = 25×1 + 2
25 = 2×7 + 11
则:
11 = 25 - 2×7
= 25 - (27-25) ×7
= 25×8 - 27×7
所以a=8, c=7
代入x = 25a + 12 = 27c + 23 得:
x = 212
Obtenez l'équation combinée x = 212 + 25 × 27t, c'est-à-dire: x ≡ 212 (mod 675)
, puis fusionnez avec x ≡ 9 (mod 26)
x = 212 + 675t = 26b + 9
26b - 675t = 203
675 = 26×25+25
25 = 25×1
所以:
203 = (26-25)×203
= (26 - (675-26*25))×203
= 26×5278 - 675×203
b=5278 , t=203
代入得x = 137237
L'équation combinée x = 137237 + 25 × 27 × 26t est obtenue: x ≡ 137237 (mod 17550), x = 14387
x = 14387 + 17550n (n∈Z)
Mission 2:
Résolvez les équations de congruence suivantes:
13x ≡ 4 (mod 99)
15x ≡ 56 (mod 101)
Ce genre d'équations de congruence avec des coefficients rend les gens intimidants, mais cela n'empêche pas l'utilisation d'Euclidienne étendue,
supprimez d'abord les coefficients:
x ≡ 46 (mod 99)
x ≡ 98 (mod 101)
求解方法很多,这里列举利用二元一次不定方程方法:
13x ≡ 4 (mod 99) 转化为 13x-99y = 4
然后用拓展欧几里德:
13×46-99×6 = 4
x=46, y=6
所以不定方程13x-99y = 4 的所有解为
x=46 + 99t
y=6+13t
所以原同余方程解为:x ≡ 46 (mod 99)
Éliminez x pour obtenir: 99a-101b = 52
Développez Euclidienne pour vous accompagner: x = 7471 (mod 9999)
x = 9999 n + 7471 (n ∈ Z)