Table des matières
Étape 1 : Construisez une pile
Concernant les questions Top-k :
Avant-propos :
Dans le blog précédent, nous avons déjà un concept préliminaire de "Heap", nous pouvons ensuite utiliser "Heap" pour résoudre les problèmes de notre vie quotidienne. Dans cet article, nous donnons respectivement deux scénarios d'application couramment utilisés. Il s'agit de "Trier " et "Top-k Problem". Le blog précédent se trouve dans : Simulation Implémentation du "Heap" -CSDN Blog
À propos du « Tri par tas » :
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(int* arr, int sz, int parent)
{
int child = parent * 2 + 1;
while (child < sz)
{
if (child + 1 < sz && arr[child] < arr[child + 1])
{
child++;
}
if (arr[child] > arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void AdjustUp(int* arr, int sz, int child)
{
while (child > 0)
{
int parent = (child - 1) / 2;
if (arr[parent] < arr[child])
{
swap(&arr[parent], &arr[child]);
}
child = parent;
}
}
int main()
{
int arr[] = { 2, 6, 9, 3, 1, 7 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sz, i);
}//向下调整算法
//for (int i = 1; i<sz; i++)
//{
// AdjustUp(arr, sz, i);
//}//向上调整算法
int end = sz - 1;
while (end > 0)
{
swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
--end;
}
return 0;
}Étape 1 : Construisez une pile
L'utilisation de "Heap" peut nous faciliter le tri d'un tableau donné dans le désordre. Tout d'abord, nous devons sélectionner un grand tas pour l'opération de tri.
Pourquoi ne choisissons-nous pas d'utiliser un petit tas pour construire un tas ?
Selon l'explication précédente du blog sur "Tas", un petit tas signifie que l'élément supérieur est le plus petit élément et que le nombre d'autres nœuds est plus petit que le premier élément. Donc s'il s'agit d'un petit tas, le plus petit nombre est déjà le premier élément. Si vous souhaitez trouver le plus petit élément suivant, vous devez construire un tas parmi les éléments restants et répéter le cycle pour terminer le tri. Cela a une complexité temporelle élevée et n'est pas propice au tri.
Par conséquent, nous choisissons d'utiliser un grand tas pour construire un tas. Après avoir réalisé un grand tas, nous échangeons le premier et le dernier élément, puis utilisons la méthode d'ajustement vers le bas pour ajuster les n-1 éléments restants, puis les échangeons. peut réaliser le tri.
int arr[] = { 2, 6, 9, 3, 1, 7 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = 1; i<sz; i++)
{
AdjustUp(arr, sz, i);
}Ajustez le tableau comme indiqué dans la figure vers le haut pour créer un tas :

Étape 2 : Trier
Nous échangeons d’abord le premier et le dernier élément :
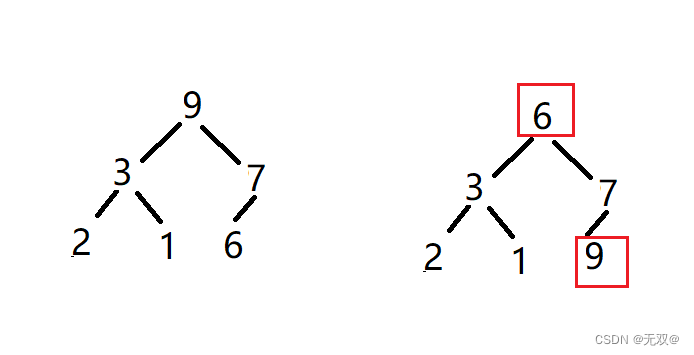
Ajustez vers le bas sur tous les éléments sauf le dernier pour continuer dans une grosse pile


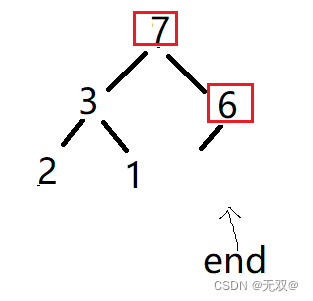
Répétez les étapes ci-dessus
Le tas final est :

Ceci termine le tri en tas.
"Problème Top-K"
Concernant les questions Top-k :
Il s'agit de trouver les K premiers éléments les plus grands ou les plus petits éléments d'une combinaison de données.En général, la quantité de données est relativement importante .
Par exemple : les 10 meilleurs professionnels, Fortune 500, liste riche, les 100 meilleurs joueurs actifs dans le jeu, etc. Prenons l'exemple de la recherche des K premiers éléments les plus grands dans n données pour illustrer : (en supposant n=10 000) (en supposant k=10)
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
const char* file = "data.txt";
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(int* arr, int sz, int parent)
{
int child = 2 * parent + 1;
while (child < sz)
{
if (child + 1 < sz && arr[child + 1] < arr[child])
{
child++;
}
if (arr[child] < arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void CreateFile()
{
//创建随机数的种子
srand((unsigned int)time(NULL));
FILE* Fin = fopen(file, "w");
if (Fin == NULL)
{
perror("Fopen error");
exit(-1);
}
int n = 10000000;
for (int i = 0; i < n; i++)
{
int x = (rand() + i) % n;
fprintf(Fin, "%d\n", x);
}
fclose(Fin);
Fin = NULL;
}
void Print()
{
FILE* Fout = fopen(file, "r");
if (Fout == NULL)
{
perror("Fout error");
exit(-1);
}
//取前k个数进小堆
int* minheap = (int*)malloc(sizeof(int) * 5);
if (minheap == NULL)
{
perror("minheap -> malloc");
return;
}
for (int i = 0; i < 5; i++)
{
fscanf(Fout, "%d", &minheap[i]);
}
for (int i = (5-1-1)/2; i >=0; --i)
{
AdjustDown(minheap, 5, i);
}
//读取数据
int x = 0;
while (fscanf(Fout, "%d", &x) != EOF)
{
if (minheap[0] < x)
{
minheap[0] = x;
}
AdjustDown(minheap, 5, 0);
}
for (int i = 0; i < 5; i++)
{
printf("%d ", minheap[i]);
}
fclose(Fout);
Fout = NULL;
}
int main()
{
//CreateFile();
Print();
return 0;
}Tout d'abord, nous créons 1 000 000 de nombres aléatoires, puis modifions les nombres, sélectionnons au hasard 5 nombres et les modifions comme
10000001,10000002,10000003,10000004,10000005
Construisez un autre petit tas . Notez qu’il doit s’agir d’un petit tas !
Si nous construisons un grand tas, si les données sont recherchées en premier et que 10000005 est trouvé, alors le nombre doit être en haut du tas. Lorsque nous trouvons le plus petit nombre suivant, nous ne pouvons pas entrer dans le tas, nous utilisons donc un petit tas !
Ensuite, placez les 5 premiers éléments des données dans le petit tas,
Ensuite, parcourez et comparez les nombres 9999995 restants. S'ils sont supérieurs à l'élément supérieur du tas, remplacez-les directement.
Après le remplacement, ajustez à nouveau vers le bas. Après avoir parcouru toutes les données, le tas sera inséré.
10000001,10000002,10000003,10000004,10000005