Ouvrir la boîte noire des réseaux de neurones

L'équipe de la communauté open source chinoise a réalisé sa première diffusion en direct, racontant l'histoire de la communauté open source chinoise au nom du partage.

réseau neuronal convolutif

Chaque noyau de convolution extrait différentes caractéristiques . Chaque noyau de convolution convolutionne l'entrée pour générer une carte de fonctionnalités reflète les fonctionnalités extraites par le noyau de convolution à partir de l'entrée. Différentes cartes de fonctionnalités montrent différentes fonctionnalités dans l'image.

1. Extraction du noyau de convolution superficielle : caractéristiques des pixels sous-jacentes telles que les bords, les couleurs et les correctifs ;
2. Extraction du noyau de convolution de niveau intermédiaire : caractéristiques de texture de niveau intermédiaire telles que des rayures, des lignes, des formes, etc. ;
3. Extraction du noyau de convolution de haut niveau : fonctionnalités sémantiques de haut niveau telles que les yeux, les pneus, le texte, etc.

Enfin, la couche de sortie de classification génère le résultat de classification le plus abstrait.

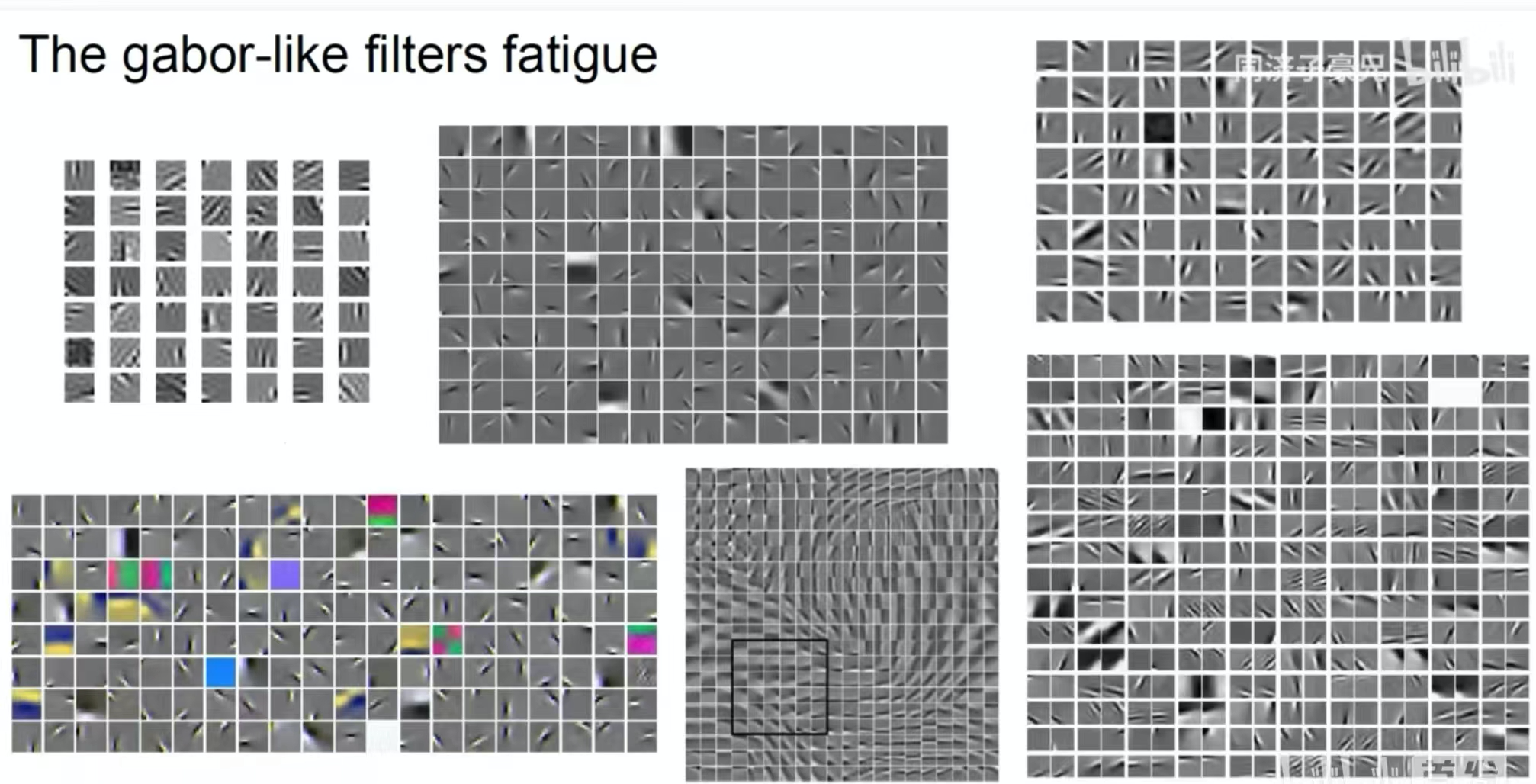
L'image ci-dessus montre les caractéristiques extraites par un noyau de convolution superficiel. Nous pouvons voir que certains noyaux de convolution extraient des formes et d'autres des couleurs. Il s'agit d'une fonctionnalité de convolution similaire au filtre de Gabor.

L'image ci-dessus montre les caractéristiques extraites par les noyaux de convolution moyenne et profonde. Le noyau de convolution intermédiaire extrait des blocs de couleur et de texture plus grands ; les caractéristiques extraites par le noyau de convolution profonde peuvent inclure des humains ou des choses concrètes.

Interprétabilité CAM

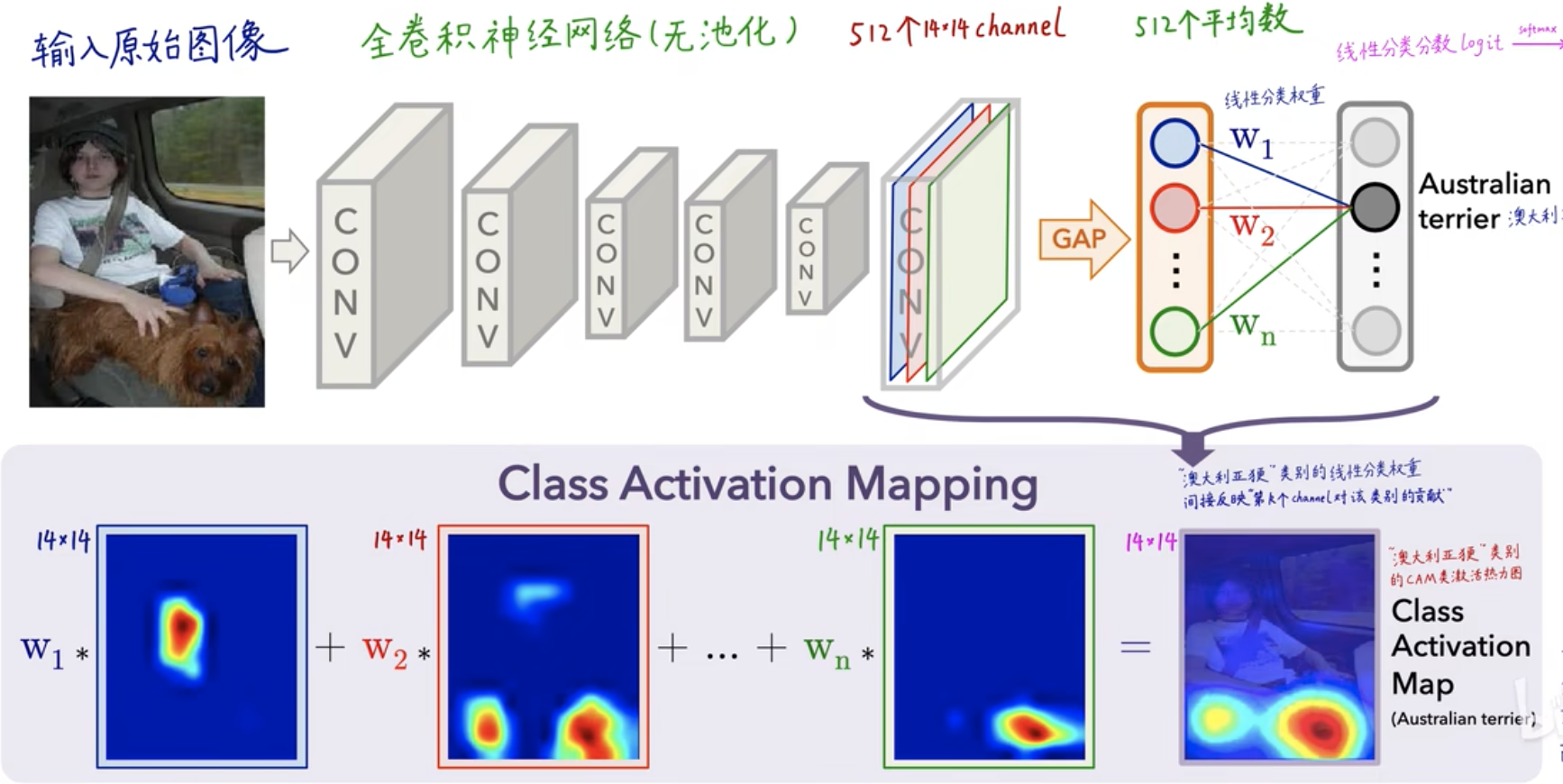
Dans la figure ci-dessus, l'image originale d'entrée a été convoluée couche par couche. Au niveau de la dernière couche, il y aura 512 noyaux de convolution et 512 canaux, c'est-à-dire que 512 caractéristiques profondes ont été extraites . Après GAP (global Average Pooling), le Une moyenne est calculée pour chaque caractéristique de canal, puis le poids (coefficient) de chaque valeur de caractéristique est obtenu via la couche FC (couche entièrement connectée) - \(W_1, W_2, W_3,..., W_n\) , pour chaque catégorie Vous pouvez obtenir une valeur de score (score), qui est obtenue par

\(score=W_1*valeur propre bleue+W_2*valeur propre rouge+...+W_n*valeur propre verte\)

Obtenu, et enfin calculé une valeur de probabilité via softmax, qui est un processus de classification CNN pour la carte thermique CAM, cela se reflète principalement dans \(W_1, W_2, W_3,..., W_n\)le poids de la valeur de la caractéristique .

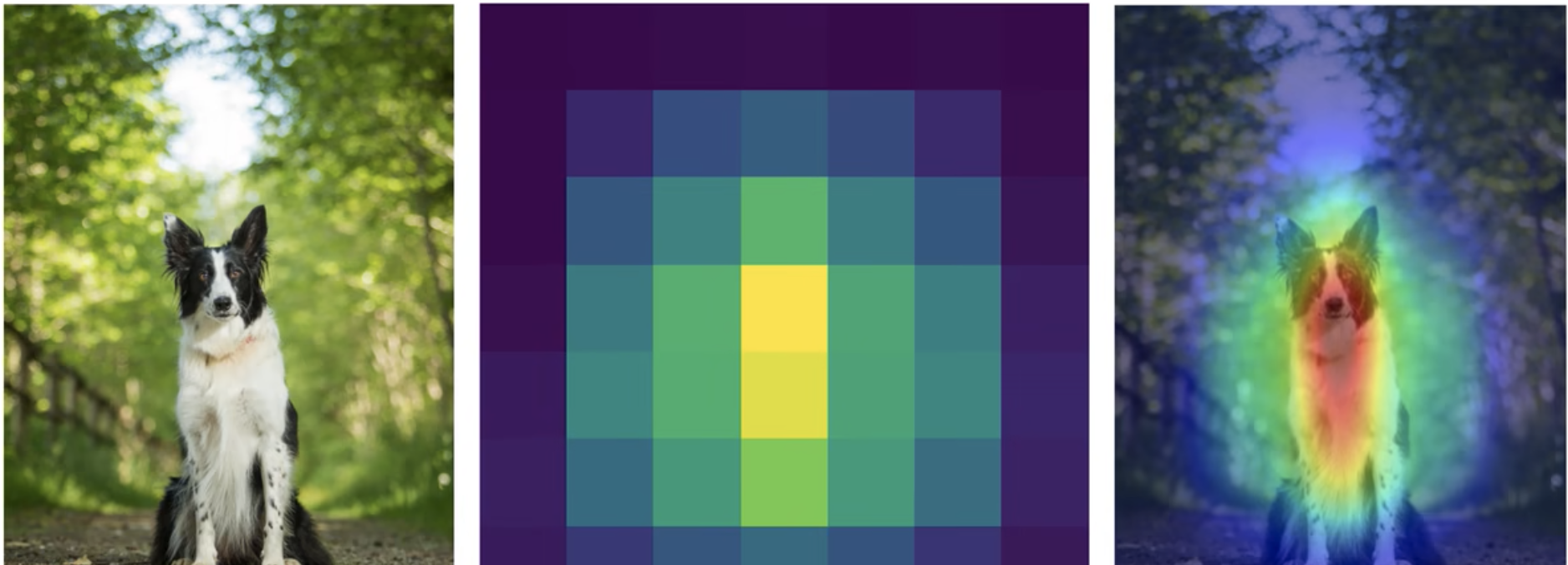
• Inconvénients de la CAM

1. Il doit y avoir une couche GAP, sinon la structure du modèle doit être modifiée et recyclée.
2. Seule la sortie de la dernière couche convolutive peut être analysée et la couche intermédiaire ne peut pas être analysée.
3. Tâches de classification d'images uniquement

DiplôméCAM

Dans GradCAM, au lieu d'utiliser la couche GAP, vous pouvez utiliser entièrement la couche FC pour sortir la partition via la couche entièrement connectée, représentée par \(y^c\) .

• Dérivée d'une matrice

1. La dérivée d'une fonction scalaire par rapport à un vecteur :

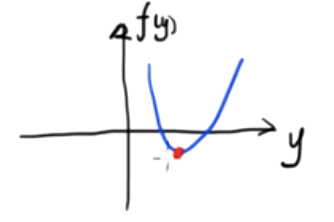
Il s'agit d'une fonction scalaire bidimensionnelle. Nous savons que la valeur minimale de cette fonction est.

\({df(y)\over dy}=0\)

Si cette fonction est une fonction scalaire tridimensionnelle composée de deux variables indépendantes, l'image est la suivante

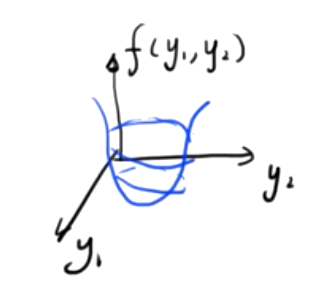
Trouver la valeur minimale de cette fonction binaire, simultanément

1. \({∂f(y_1,y_2)\over ∂y_1}=0\)
2. \({∂f(y_1,y_2)\over ∂y_2}=0\)

Si une fonction scalaire a n variables indépendantes \(f(y_1,y_2,y_3,...,y_n)\) , on définit un vecteur

Oui=[ ]

Alors la dérivée partielle de la fonction par rapport au vecteur Y peut être définie comme

\({∂f(Y)\over ∂Y}=\) \([\) \(]\)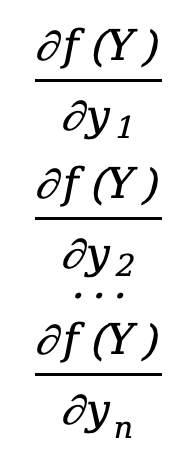

Il s'agit d'un vecteur colonne n*1, et nous constatons que son nombre de lignes est le même que le dénominateur Y. Cette disposition est appelée disposition du dénominateur .

De même, on peut également définir la dérivée partielle de la fonction par rapport au vecteur Y comme

\({∂f(Y)\sur ∂Y}=[{∂f(Y)\sur ∂y_1}{∂f(Y)\sur ∂y_2}...{∂f(Y)\sur ∂y_n }]\)

Il s'agit d'un vecteur de ligne 1*n, et nous constatons que son nombre de lignes est le même que le numérateur f(Y) (un scalaire 1*1. Une telle disposition est appelée disposition du numérateur .

La disposition du dénominateur et la disposition du numérateur sont les transposées l'une de l'autre .

Exemple 1 : \(f(y_1,y_2)=y_1^2+y_2^2\)

Disposition du dénominateur :

Soit Y=[ ]

mais

\({∂f(Y)\over ∂Y}=\) [ ]=[ ]

Disposition moléculaire :

令\(Y=[y_1 y_2]\)

mais

\({∂f(Y)\over ∂Y}=[​{∂f(Y)\over ∂y_1} {∂f(Y)\over ∂y_2}]=[2y_1 2y_2]\)

2. Dérivée de la fonction vectorielle par rapport au vecteur

Si notre fonction est aussi un vecteur

F(Y)=[ ]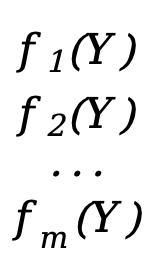

Chaque \(f_x(Y)\) (x=1,2,3,...,m) équivaut ici à une fonction scalaire f(Y) ci-dessus (la variable indépendante est le vecteur Y), F(Y ) est une fonction vectorielle de m*1.

Premier exemple :

1. Oui=[ ]
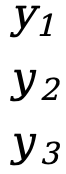2. F(Y)=[ ]=[ ]

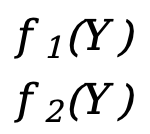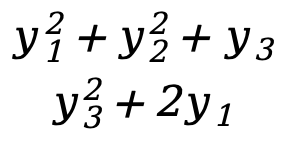Dérivée partielle d'une fonction vectorielle par rapport à un vecteur, la disposition du dénominateur est

\({∂F(Y)\over ∂Y}=\) [ ]=[ ]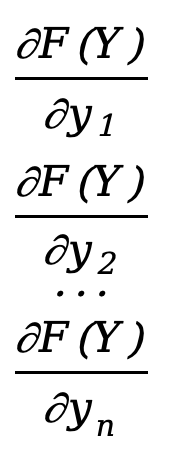   

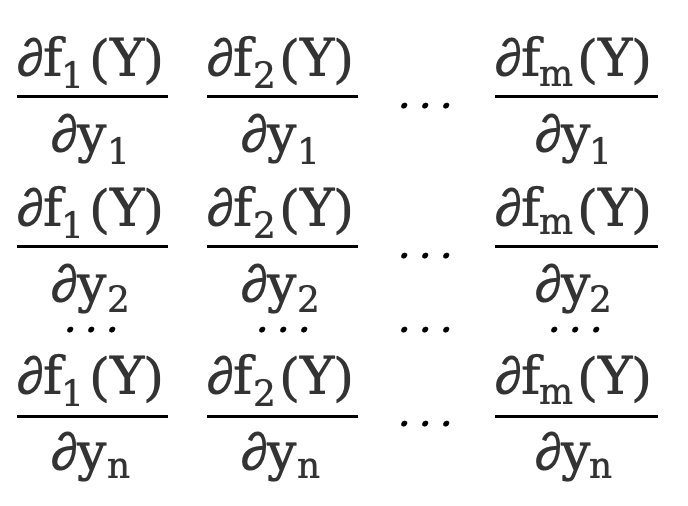Comme dans l'exemple 1, il y a

\({∂F(Y)\over ∂Y}=\) [ ]=[ ]=[ ]

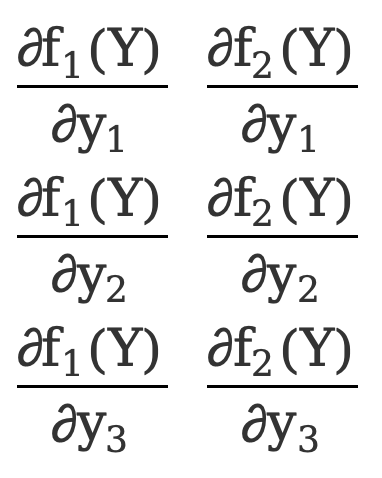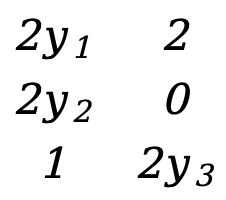Il s'agit d'une matrice 3*2.

 

Un programmeur né dans les années 1990 a développé un logiciel de portage vidéo et en a réalisé plus de 7 millions en moins d'un an. La fin a été très éprouvante ! Google a confirmé les licenciements, impliquant la « malédiction des 35 ans » des codeurs chinois des équipes Flutter, Dart et . Python Arc Browser pour Windows 1.0 en 3 mois officiellement la part de marché de GA Windows 10 atteint 70 %, Windows 11 GitHub continue de décliner l'outil de développement natif d'IA GitHub Copilot Workspace JAVA. est la seule requête de type fort capable de gérer OLTP+OLAP. C'est le meilleur ORM. Nous nous rencontrons trop tard.

{{o.name}}

{{m.nom}}