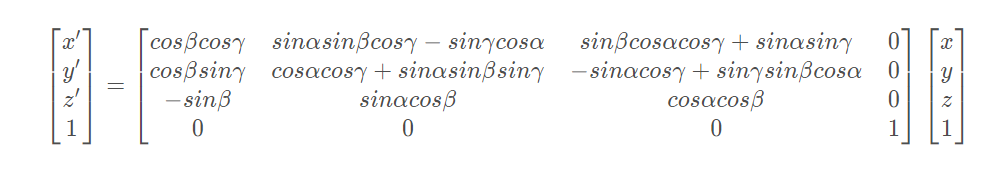カメラキャリブレーション（2）4つの座標系とそれらの変換関係の深い理解

I.はじめに

ビジョンシステムには、ピクセル平面座標系（u、v）、画像座標系（x、y）、カメラ座標系（Xc、Yc、Zc）、世界座標系（Xw、Yw、Zw）の4つの座標系があります。下に示された。各座標系の間には接続があるため、画像のピクセル座標を介して世界座標系の座標を見つける方法は、カメラのキャリブレーションによって解決する必要があります。重要なアルゴリズムの部分は座標系の変換であり、変換は均一に合格する必要があります。コーディネート完了する方法を表現します。

2、座標系の変換

2.1ピクセル座標系と画像座標系の変換

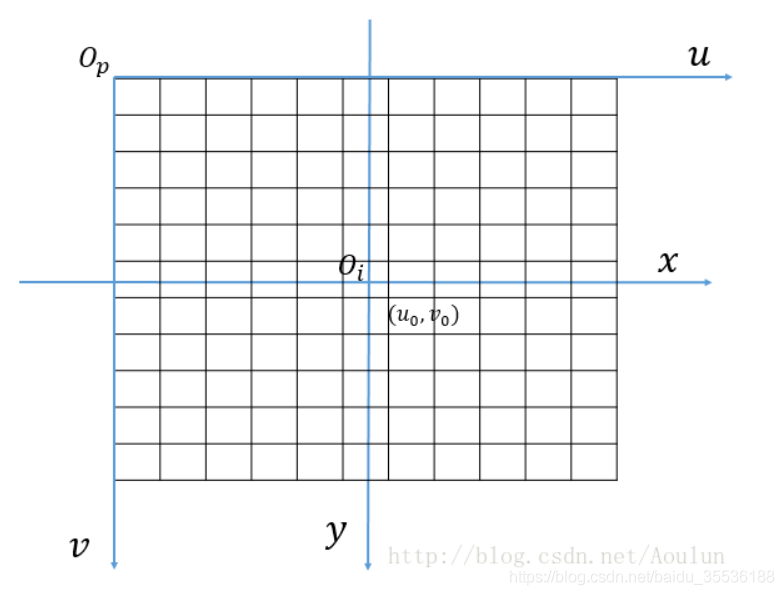
ピクセル座標は、画像内のピクセルの位置です。ピクセル座標系は画像内で確立されており、カメラ座標系で変換する必要があり、その単位はピクセルです。左上隅の頂点が原点（Op）、右の水平方向がu、下向きの垂直方向がv軸です。
画像座標系の単位はミリメートルです。これは、ピクセル座標が画像内の点の特定のサイズを反映できないため、それを表すために画像座標系が必要になるためです。原点はOiであり、これは光軸とイメージング平面。
両方の座標系はイメージング平面上にありますが、それらの原点と測定単位は異なります。変換中に2つのパラメータ（dx、dy）を知る必要があります。これらはそれぞれ、感光チップ上のピクセルの実際のサイズを表します。

2つの間の変換には、単位変換が必要です。この図では、画像の中心のピクセル座標が（u0、v0）であると仮定すると、画像の座標系の座標（x、y）とピクセル座標系の座標（u、v）の関係は次のようになります。次のように表現されます：
$u=x/dx+u0$
$v=y/dy+v0$
を同次座標に変換します：
$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$= $\left[\begin{array}{ccc}1/dx& 0& u0\\ 0& 1/dy& v0\\ 0& 0& 1\end{array}\right]$* $\left[\begin{array}{c}バツ\\ Y\\ 1\end{array}\right]$

2.2カメラ座標系と画像座標系間の変換

カメラの座標系は、カメラの光軸をZ軸とします。カメラの光学系における光の中心位置は、原点Oc（実際にはレンズの中心）です。横軸Xcと縦軸Ycはカメラの座標系はそれぞれ画像の座標系にあります。X軸とY軸は平行で、OcOi間の距離はfです。
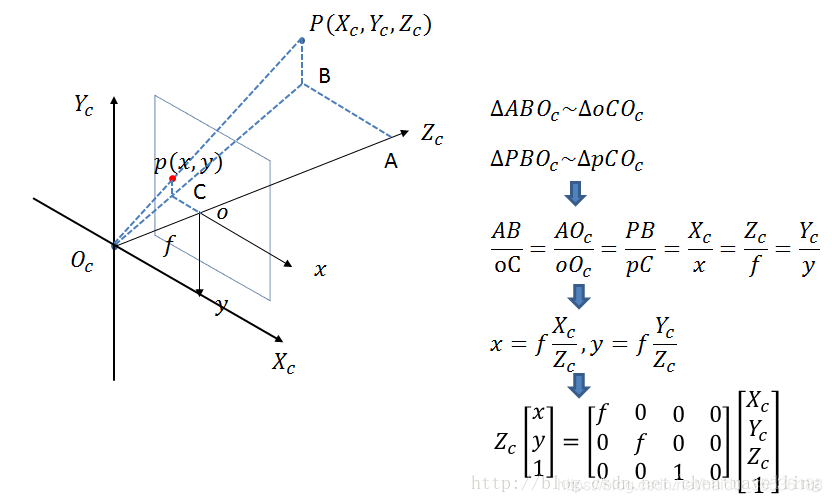上図の点Pは画像点の座標、Bはカメラ座標系の物体の座標であり、上図に示すように同様の三角形で解き、最終的に同次座標で表すことができます。最後の式は、カメラの座標系が3次元であり、画像の座標系が2次元であることを示しています。これは、同次座標変換の形式でのみアップグレードできます。
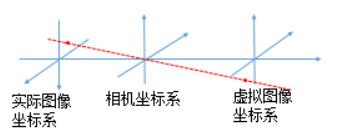
では、なぜピクセル座標系がカメラ座標系の前にあるのでしょうか。概略図
から、像面が鏡の右側にあることがわかります。カメラ校正の座標系の関係を導き出すとき、光は最初に像面を通過し、次に収束すると考えられます。カメラの座標系上のポイント。その理由は、導出において、像面が虚像面に置き換えられるためである。

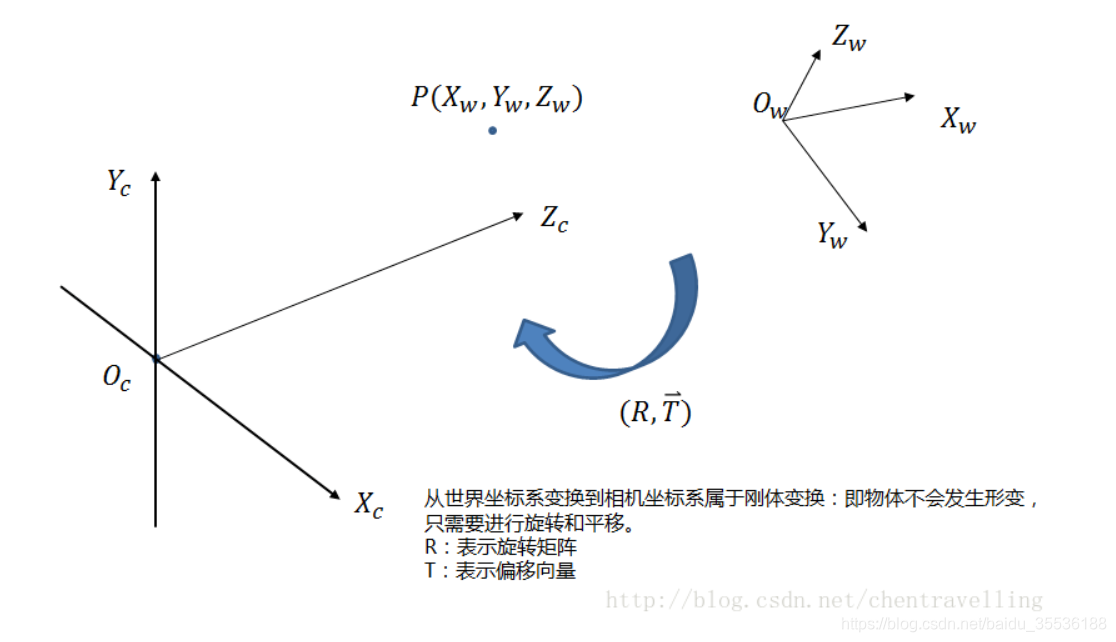
2.3世界座標系とカメラ座標系間の変換

ワールド座標系は、対象物の位置の基準系であり、計算の都合に合わせて自由に配置できます。単位は、mmなどの長さの単位です。ワールド座標系からカメラ座標系への変換には、回転と平行移動が含まれます（実際、すべての動きは回転行列と平行移動ベクトルで表すこともできます）。ワールド座標系とカメラ座標はどちらも右手座標系であるため、変形されません（剛体変換）。

計算プロセス：
平行移動、カメラ座標点（Xc、Yc、Zc）から世界座標点（Xw、Yw、Zw）までの平行移動距離（tx、ty、tz）：
$\left[\begin{array}{c}Xw\\ ワット\\ wから\\ 1\end{array}\right]$= $\left[\begin{array}{cccc}1& 0& 0& tx\\ 0& 1& 0& ty\\ 0& 0& 1& tz\\ 0& 0& 0& 1\end{array}\right]$* $\left[\begin{array}{c}Xc\\ そしてc\\ Zc\\ 1\end{array}\right]$
座標点（Xc、Yc、Zc）は、変換プロセス中にワールド座標点（Xw、Yw、Zw）に対して特定の角度で回転します。
最初に、基本回転行列と基本行列が与えられます
。R= $\left[\begin{array}{cc}COS\theta & sの私のn\theta \\ -sの私のn\theta & -COS\theta \end{array}\right]$
基本着阵：
$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$
座標点（Xc、Yc、Zc）がそれぞれX、Y、Z軸を中心にα、β、γ度回転した場合、最終的な式は次のようになります（笑、アフィン変換を導出したくない）自分で式を作成し、最終結果を出すだけです。リンクは以下のとおりです）：

次に、変換変換を次のように組み合わせることができます。

2.4ピクセル座標系から世界座標系への変換（最終変換）

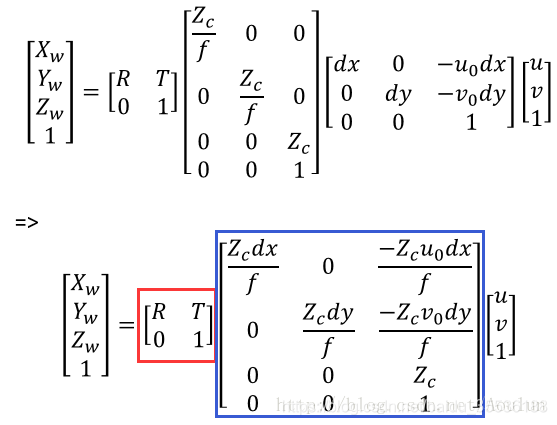
赤いボックスは外部パラメータ、RとTはそれぞれ回転と平行移動です。
内部パラメータはカメラの固有のプロパティであり、実際には焦点距離f、ピクセルサイズdx、dyです。
Zcは明らかです、それは光軸からの点の距離を意味します。

参考記事：
カメラのキャリブレーションと
3D変換でのキャリブレーション結果の使用方法基本：平行移動、回転、ズーム（アフィン変換）の詳細な説明-式の導出
コンピュータービジョン：カメライメージングの原理：世界座標系、カメラ座標系、画像間の変換座標系とピクセル座標系