ハルビン工業大学 2022 機械学習実験 1: カーブ フィッティング

この実験の要件は非常に明確です (前学期と比較して)。このブログは python で実装されており、科学計算ライブラリが使用されnumpy、図面が使用されていmatplotlib.pyplotます。簡単にするために、ファイルの先頭に次のものをインポートします。

import numpy as np
import matplotlib.pyplot as plt

この実験で使用した numpy 関数

一般に(import numpy as np)numpyと略されます。np以下は、実験で使用された numpy 関数の簡単な紹介です。次のコードを先頭に追加する必要がありますimport numpy as np。

np.array

この関数は、numpy.ndarray多次元配列として理解できるオブジェクトを返します (この実験では、1 次元 (列ベクトルと見なすことができる) と 2 次元 (行列) のみが使用されます)。\pmb x の下に小文字の x を使用します$バツx$は列ベクトル、大文字$A$は行列を表します。AAA.Tを意味します$A$の転置ペアndarrayは、通常、要素単位です。

>>> x = np.array([1,2,3])
>>> x
array([1, 2, 3])
>>> A = np.array([[2,3,4],[5,6,7]])
>>> A
array([[2, 3, 4],
       [5, 6, 7]])
>>> A.T # 转置
array([[2, 5],
       [3, 6],
       [4, 7]])
>>> A + 1
array([[3, 4, 5],
       [6, 7, 8]])
>>> A * 2
array([[ 4,  6,  8],
       [10, 12, 14]])

np.ランダム

np.randomこのモジュールには、乱数を生成するための関数がいくつか含まれています。この実験では、ランダムな初期化パラメーター (勾配降下法) を使用して、データにノイズを追加します。

>>> np.random.rand(3, 3) # 生成3 * 3 随机矩阵，每个元素服从[0,1)均匀分布
array([[8.18713933e-01, 5.46592778e-01, 1.36380542e-01],
       [9.85514865e-01, 7.07323389e-01, 2.51858374e-04],
       [3.14683662e-01, 4.74980699e-02, 4.39658301e-01]])
      
>>> np.random.rand(1) # 生成单个随机数
array([0.70944563])
>>> np.random.rand(5) # 长为5的一维随机数组
array([0.03911319, 0.67572368, 0.98884287, 0.12501456, 0.39870096])
>>> np.random.randn(3, 3) # 同上，但每个元素服从N(0, 1)（标准正态）

数学関数

この実験でのみ使用されnp.sinます。これらの数学関数np.ndarrayは要素ごとに動作します。

>>> x = np.array([0, 3.1415, 3.1415 / 2]) # 0, pi, pi / 2
>>> np.round(np.sin(x)) # 先求sin再四舍五入: 0, 0, 1
array([0., 0., 1.])

さらに、python のライブラリに似たnp.log関数があります (多次元配列の要素単位の操作のみ)。np.expmath

np.dot

2 つの行列の積を返します。線形代数の行列乗算と一致します。最初の行列の列は、2 番目の行列の行数と同じである必要があります。特に、そのうちの 1 つが 1 次元配列の場合、形状は自動的に$n\times 1$または$1\times n.$

>>> x = np.array([1,2,3]) # 一维数组
>>> A = np.array([[1,1,1],[2,2,2],[3,3,3]]) # 3 * 3矩阵
>>> np.dot(x,A)
array([14, 14, 14])
>>> np.dot(A,x)
array([ 6, 12, 18])

>>> x_2D = np.array([[1,2,3]]) # 这是一个二维数组（1 * 3矩阵）
>>> np.dot(x_2D, A) # 可以运算
array([[14, 14, 14]])
>>> np.dot(A, x_2D) # 行列不匹配
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<__array_function__ internals>", line 5, in dot
ValueError: shapes (3,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)

np.eye

np.eye(n)次数 n の単位行列を返します。

>>> A = np.eye(3)
>>> A
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

線形代数相関

np.linalg線形代数関連のライブラリです。

>>> A
array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])
>>> np.linalg.inv(A) # 求逆（本实验不考虑逆不存在）
array([[1.        , 0.        , 0.        ],
       [0.        , 0.5       , 0.        ],
       [0.        , 0.        , 0.33333333]])
>>> x = np.array([1,2,3])
>>> np.linalg.norm(x) # 返回向量x的模长（平方求和开根号）
3.7416573867739413
>>> np.linalg.eigvals(A) # A的特征值
array([1., 2., 3.])

データの生成

データを生成するには、ノイズ (エラー) を追加する必要があります。クラスで与えられた例は正弦関数で、標準の正弦関数$よ=罪x.$ (ノイズを追加すると、$よ=罪バツ+\epsilon 、$ ε ∼ N ( 0 ,$ϵ～N(0,p^2)$、$罪x$の最大値$1$では、誤差の分散が小さくなるように設定します。ここでは$\frac{}{25}$）。

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1], 默认为(0, 10)
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    # np.random.rand 产生[0, 1)的均匀分布，再根据l, r缩放平移
    # 这里sort是为了画图时不会乱，可以去掉sorted试一试
    x = sorted(np.random.rand(N) * (r - l) + l)
	
	# np.random.randn 产生N(0,1)，除以5会变为N(0, 1 / 25)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

結果のデータセットには、行ごとに平面上のポイントがあります。結果のデータは次のようになります。

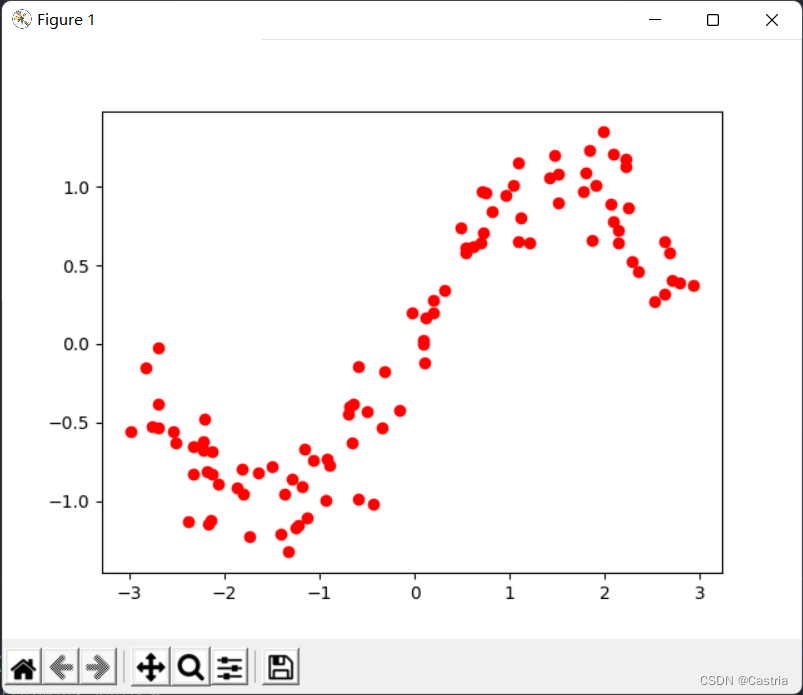
漠然と正弦関数の形になっています。上記の画像を生成するコードは次のとおりです。

dataset = get_dataset(bound = (-3, 3))
# 绘制数据集散点图
for [x, y] in dataset:
    plt.scatter(x, y, color = 'red')
plt.show()

最小二乗フィッティング

以下では、4 つの方法 (最小二乗、正則項/リッジ回帰、勾配降下、共役勾配) を使用して、上記の摂動正弦波を多項式で近似します。

分析ソリューションの導出

最小二乗法の原理を思い出してください$次数m$の多項式
$$f\left(x\right)={の}_{}+{の}_{}バツ+{の}_{}{バツ}^2+...+{の}_{}{バツ}^m$$
を使用して、真の関数$よ=罪x.$私たちの目標は、データセット$({\times }_{}、{よ}_{})、({\times }_{}、{よ}_{})、...,({\times }_{}、{よ}_{})$損失$L$ (損失)、ここで、損失関数は二乗誤差を取ります:
$$L=\sum _{私は=1}[{と}_{}-f(x_{}){]}^2$$
パラメータ${の}_{}、{の}_{}、...,{の}_{}、$損失$L$关于${の}_{}、{の}_{}、...,{の}_{}$の導関数。便宜上、線形代数表記を使用します:
$$バツ={⎝\begin{array}{ccccc}1& {バツ}_{}& {バツ}_1^{}& \cdots & {バツ}_1^{}\\ 1& {バツ}_{}& {バツ}_2^{}& \cdots & {バツ}_2^{}\\ ⋮& & & & ⋮\\ & {バツ}_{}& {バツ}_N^{}& & {バツ}_N^{}\end{array}⎠}_{N\times (m+1}、よ={⎝\begin{array}{c}{よ}_{}\\ {よ}_{}\\ ⋮\\ {よ}_{}\end{array}⎠}_{N\times }、の={⎝\begin{array}{c}{の}_{}\\ {の}_{}\\ ⋮\\ {の}_{}\end{array}⎠}_{(m+1)\times }.$$
この表現の下では、
$$⎝\begin{array}{c}f\left(x_{}\right)\\ f\left(x_{}\right)\\ ⋮\\ f(x_{}\end{array}⎠=XW.$$
疑問がある場合は、行列の乗算で自分で確認できます。続いて、誤差項の合計は次のように表すことができます
$$⎝\begin{array}{c}f\left(x_{}\right)-{よ}_{}\\ f\left(x_{}\right)-{よ}_{}\\ ⋮\\ f\left(x_{}\right)-{よ}_{}\end{array}⎠=XW-Y.$$
したがって、損失関数
$$L=(XW-と{）}^T(XW-Y).$$
(ベクトル$バツバツ=({\times }_{}、{バツ}_{}、...,{バツ}_{}{)}^{}$x \pmb x${}^{に使用できるT}$のコンポーネントの二乗和$バツx$は内積、つまり${バツバツ}^Tバツx.$ )LL
を得るために$L$最小$w$ (この$W$は列ベクトルです)、私たちはする必要があり$L$の偏導関数を$0:$
$$\begin{array}{rl}\frac{\partial L}{\partial W}& =\frac{}{\partial W}[(XW-と{）}^T(XW-や）]\\ & =\frac{}{\partial W}[(W^T{X}^T-{よ}^T\left)\right(XW-や）]\\ & =\frac{}{\partial W}({W.}^T{X}^T\times W-{の}^T{X}^{T}Y-{よ}^T\times W+{よ}^{T}Y)\\ & =\frac{}{\partial W}({W.}^T{X}^T\times W-2{年}^T\times W+{よ}^{T}Y)(簡単に確認できます。{の}^T{X}^{T}Y={よ}^T\times W、したがって、組み合わせることができます）\\ & =2{\times }^T\times W-2{\times }^T\end{array}$$
説明: (1) WTXTYW^TX^TY
により、3 行目から 4 行目まで${の}^T{X}^{T}Y$和${よ}^{T}XW$はすべて数字 (または$1\times 1$行列)、2つは互いに転置されるため、値は同じであり、1つの項目に結合できます。
(2) 行 4 から行 5 までの行列の導出、第 1 項$\frac{}{\partial W}\left({W.}^T\right(X^{T}X\left)W\right)$は$W$の二次形式で、その導関数は$2{\times }^{T}XW.$
(3) 一次項の場合$-2{年}^{T}XW$は、実数体による導出の場合、$-2{年}^{T}X.$しかし、行列の型が正しくないことを確認してください. 転置を行う必要があります$-2{\times }^{T}Y.\_$

行列線形代数は、クラスで体系的に教えられていません。ここに表示される内容を説明するためだけです。(それ以上ある場合はしません)
偏導関数を 0 とすると、
$${バツ}^T\times W={よ}^{T}X、$$
左乗算$(X^{T}X{)}^{-1}$（${バツ}^{T}X$の可逆性については、以下の補足を参照してください
$$の=(X^{T}X{)}^{-1}{\times }^{T}Y.$$
これが私たちの$W$の解析解については、関数を呼び出してこの値を計算するだけです。

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)

コードを少し説明します。最初の行は、上記で同意したXXを生成しますデータセット( x 1 , x 2 , . . . , x N ) T (x_1,x_2,...,x_N)^Tdataset[:,0]の 0 番目の列である$X$行列$({\times }_{}、{バツ}_{}、...,{バツ}_{}{)}^T$ ; 2 行目は$Y$行列。3 行目は上記の解析解を返します。(Python の構文やnumpyライブラリに慣れていない場合は、かなり不親切です)

完了した関数の結果を確認するだけです。これを行うには、まず、取得したWWdrawを変換する関数を記述します。$W$に対応する多項式$f\left(x\right)$pyplotをライブラリ イメージ描画

'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

次に、主な機能:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 最小二乘
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')
    
	# 绘制图像
    plt.legend()
    plt.show()

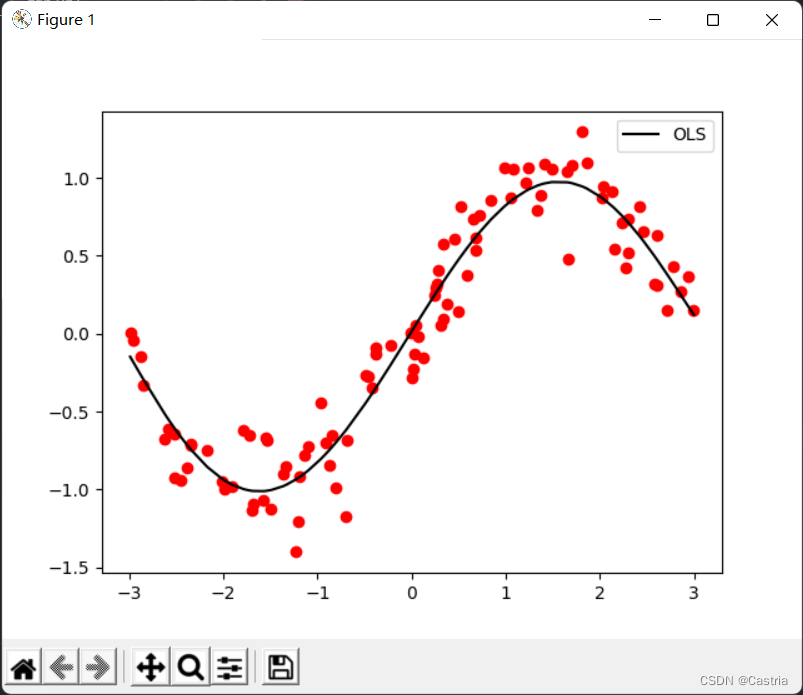
5 次多項式フィッティングの効果が非常に優れていることがわかります (データ セットは毎回ランダムに生成されるため、最初の図とは異なります)。

この部分のすべてのコードの時点で、同じ名前の次の関数は記述されていません。

import numpy as np
import matplotlib.pyplot as plt

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1]
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    x = sorted(np.random.rand(N) * (r - l) + l)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)
'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

if __name__ == '__main__':

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')

    plt.legend()
    plt.show()

補足説明

上記の部分はそれほど厳密ではありません: 行列$X$の場合、${バツ}^{T}X$は必ずしも可逆ではありません。ただし、この実験では、それが可逆行列であることを示すことができます。このクラスは線形代数のクラスではないので、これにはあまり多くのスペースを割きません
。$X$は$N\times (メートル+1)$行列の。ここで、データ数は$N$は多項式の次数mmよりもはるかに大きい$m$、$N>メートル+1;$
(2)${バツ}^{T}X$は可逆です。説明が必要です$(X^{T}X{)}_{(m+1)\times (m+1}$フルランク、つまり$R\left(X^{T}X\right)=メートル+1;$
(3) 線形代数では、$R\left(X\right)=R\left(X^T\right)=R\left(X^{T}X\right)=R\left(X{X}^T\right);$
（4）$X$はランクがmin { N , m + 1 } = m + 1. min\{N,m+1\}=m+1 にヴァンデルモンド行列$私の\{N、メートル+1\}=メートル+1.$

正規化項を追加 (リッジ回帰)

最小二乗法は過適合になりやすいです。この欠陥を説明するために、生成されたデータ セットの最初の 50 ポイントをトレーニングに使用し (サンプリングが十分に均一にならないように、ここではオーバーフィッティングを説明するだけです)、パラメーターを取得し、関数イメージ全体を描画します。フィッティング効果を確認するには:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 取前50个点进行训练
    coef1 = fit(dataset[:50], m = 3)
    # 再画出整个数据集上的图像
    draw(dataset, coef1, color = 'black', label = 'OLS')

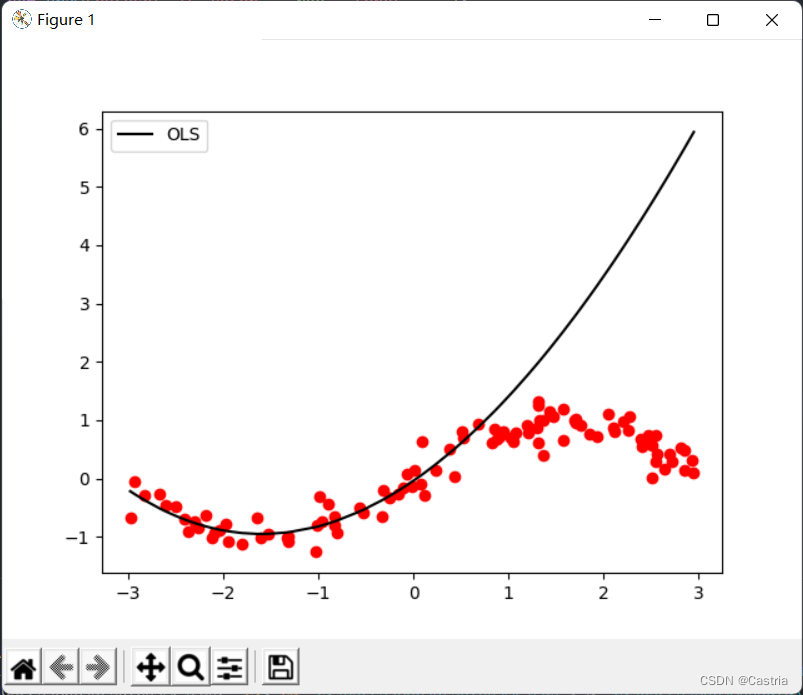
過適合 ( $これは、\; m$が大きい場合に特に深刻$メートル=3$時）。多項式の次数が増加するにつれて、与えられたデータセットにできるだけ近づけるために、計算された係数の大きさがますます大きくなり、目に見えないサンプルのパフォーマンスが低下します。上記のように、最初の 50 点 (横座標$[-3,0]$ ) は非常に良好ですが、テスト セットのパフォーマンスは非常に悪いです ($[0,3]$）。オーバーフィッティングを防ぐために、正則化項を導入できます。このとき、損失関数$L$变は
$$L=(XW-と{）}^T(XW-と）+\lambda ||W|{|}_2^{}$$
どこで$||\cdot |{|}_2^{}$L 2 L_2を示します$L_{}$ノルムの二乗、この場合は${の}^{TW};\_\lambda$は正則化係数です。この式はリッジ回帰とも呼ばれます。その考え方は、損失関数と結果のパラメーターWWを考慮に入れることです。$W$のモジュロ長($L_{}$正常)、 WWを防止$W$のパラメータが大きすぎます。

例 (数字はランダムに作成されます): 正則化係数が$1$、データセットのスキーム 1 の二乗誤差が$0.5、$このとき$の=(100,-200,300,150{）}^T$ ; データセットのスキーム 2 の二乗誤差は$10、$このとき$の=(1,-3,2、1)$の場合、 W.W.を選択します$W.$正則化係数$\lambda$はこれをWWで特徴付けます$W$係数の長さの重要性:$\lambda$が大きい$W$のモジュール長が大きいほど、ペナルティが大きくなります。λ = 0 のとき$l=0の場合、$リッジ回帰は通常の最小二乗法になります。リッジ回帰に似ているのは LASSO で、正規化項を$L_{}$標準。

上記の導出を繰り返すと、 W = ( XTX + λ E m + 1 ) − 1 XTY . W=(X^TX+\lambda E_{m+1})^{-1}X^TYとして解析解を得ることができます。
$$の=(X^{T}X+\lambda E{\_}_{m+}{)}^{-1}{\times }^{T}Y.$$
ここで${と}_{m+}$は$メートル+一$次単位行列。簡単に$(X^{T}X+\lambda E{\_}_{m+}）$もリバーシブルです。

コードのこの部分は次のとおりです。

'''
岭回归求解析解, m 为多项式次数, l 为 lambda 即正则项系数
岭回归误差为 (XW - Y)^T*(XW - Y) + λ(W^T)*W
- dataset 数据集
- m 多项式次数, 默认为 5
- l 正则化参数 lambda, 默认为 0.5
'''
def ridge_regression(dataset, m = 5, l = 0.5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + l * np.eye(m + 1)), X.T), Y)

2 つの方法の比較は次のとおりです。

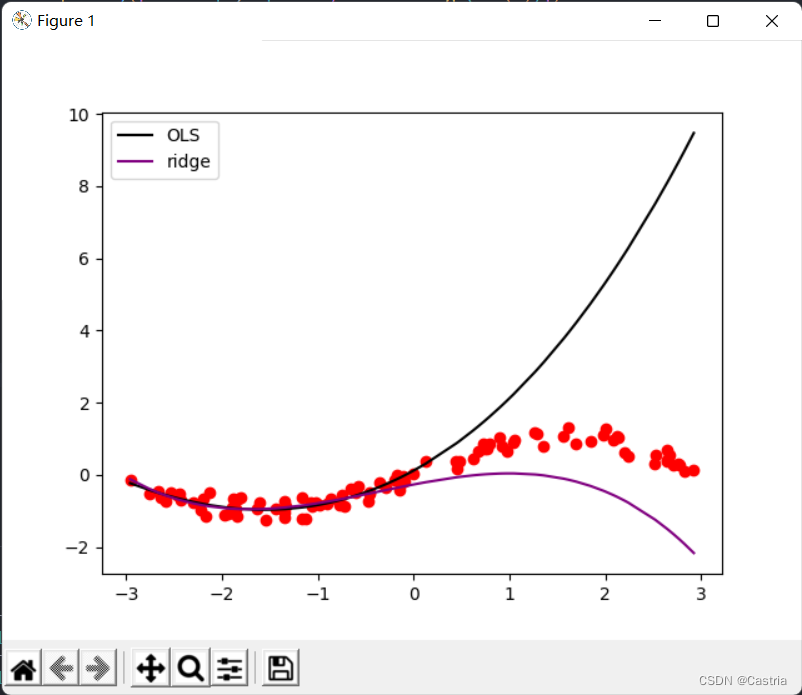
比較から、リッジ回帰がオーバーフィッティングを大幅に削減することがわかります (このとき$メートル=3、l=0.3$ )。

勾配降下法

勾配降下法は、この問題を解決する最良の方法ではなく、簡単に収束に失敗する可能性があります。最初に、勾配降下法の基本的な考え方を簡単に紹介します。複素関数f ( x ) f(x)を見つけたい場合$f\left(x\right)$の最小値 (最大点)$x$はベクトルなど)、つまり
$${バツ}_{}=\underset{バツ}{\mathrm{引数}}f\left(x\right)$$
勾配降下は次の操作を繰り返します:
(0) (ランダムに) 初期化${バツ}_{}(t=0)$ ;
(1)$f\left(x\right)$ in${バツ}_{}$での勾配 ( $x$が 1 次元の場合は微分)$\nabla f\left(x_{}\right)$；
（2）${バツ}_{t+}={バツ}_{}-\eta \nabla f\left(x_{}\right)$
(3)${バツ}_{t+}$xt x_tで${バツ}_{}$差がほとんどない（設定範囲に達する）か、反復回数が設定上限に達した場合はアルゴリズムを停止し、そうでない場合は (1) (2) を繰り返します。

其中$\eta$は勾配降下のステップ サイズを決定する学習率です。以下は、 y = x 2 y=x^2
を求める勾配降下法です。$よ={バツ}^{}$最小点${}^{2のプログラム例:}$

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return x ** 2

def draw():
    x = np.linspace(-3, 3)
    y = f(x)
    plt.plot(x, y, c = 'red')

cnt = 0
# 初始化 x
x = np.random.rand(1) * 3
learning_rate = 0.05

while True:
    grad = 2 * x
    # -----------作图用，非算法部分-----------
    plt.scatter(x, f(x), c = 'black')
    plt.text(x + 0.3, f(x) + 0.3, str(cnt))
    # -------------------------------------
    new_x = x - grad * learning_rate
    # 判断收敛
    if abs(new_x - x) < 1e-3:
        break

    x = new_x
    cnt += 1

draw()
plt.show()

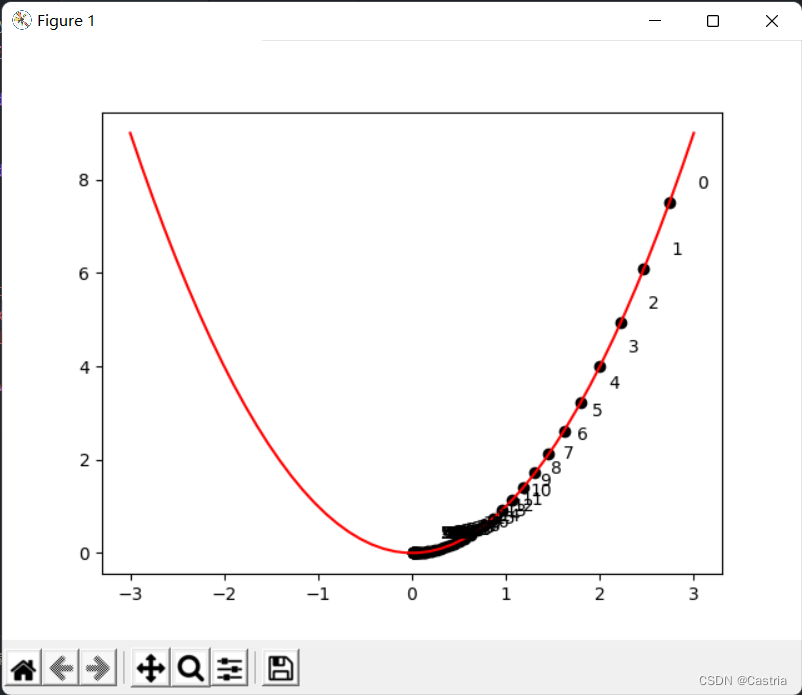
上の図はxxを示しています$x$反復が進むにつれて、$x$は、正の半軸に沿ってゼロに近づき続けます。なお、学習率はあまり大きくできませんが（上記のプログラムでは学習率を少し小さく設定していますが）、手動で調整する必要があります$x$は正と負の半軸で前後に振動し、収束しにくくなります。

最小二乗法では、最適化する必要がある関数は損失関数
$$L=(XW-と{）}^T(XW-Y).$$
次に、勾配降下法で問題を解きます。上記の導出では、
$$\begin{array}{r}\frac{\partial L}{\partial W}=2{\times }^T\times W-2{\times }^T\end{array}、$$したがって、 WW
でイテレーションを実行するたびに$W$は、パラメーターWWまでこの勾配を減算します。$W$は収束します。しかし、実験の後、二乗誤差は勾配を大きくしすぎてプロセスが収束できないため、平均二乗誤差 (MSE) を使用してそれを置き換え、元の式を$N$ :

'''
梯度下降法(Gradient Descent, GD)求优化解, m 为多项式次数, max_iteration 为最大迭代次数, lr 为学习率
注: 此时拟合次数不宜太高(m <= 3), 且数据集的数据范围不能太大(这里设置为(-3, 3)), 否则很难收敛
- dataset 数据集
- m 多项式次数, 默认为 3(太高会溢出, 无法收敛)
- max_iteration 最大迭代次数, 默认为 1000
- lr 梯度下降的学习率, 默认为 0.01
'''
def GD(dataset, m = 3, max_iteration = 1000, lr = 0.01):
    # 初始化参数
    w = np.random.rand(m + 1)

    N = len(dataset)
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = dataset[:, 1]

    try:
        for i in range(max_iteration):
            pred_Y = np.dot(X, w)
            # 均方误差（省略系数2）
            grad = np.dot(X.T, pred_Y - Y) / N
            w -= lr * grad
    '''
    为了能捕获这个溢出的 Warning，需要import warnings并在主程序中加上：
    warnings.simplefilter('error')
    '''
    except RuntimeWarning:
        print('梯度下降法溢出, 无法收敛')

    return w

このとき$m$を少し大きく (たとえば 4) 設定すると、反復中に勾配がオーバーフローし、パラメーターが収束できなくなります。収束すると、フィッティング効果は OK です。

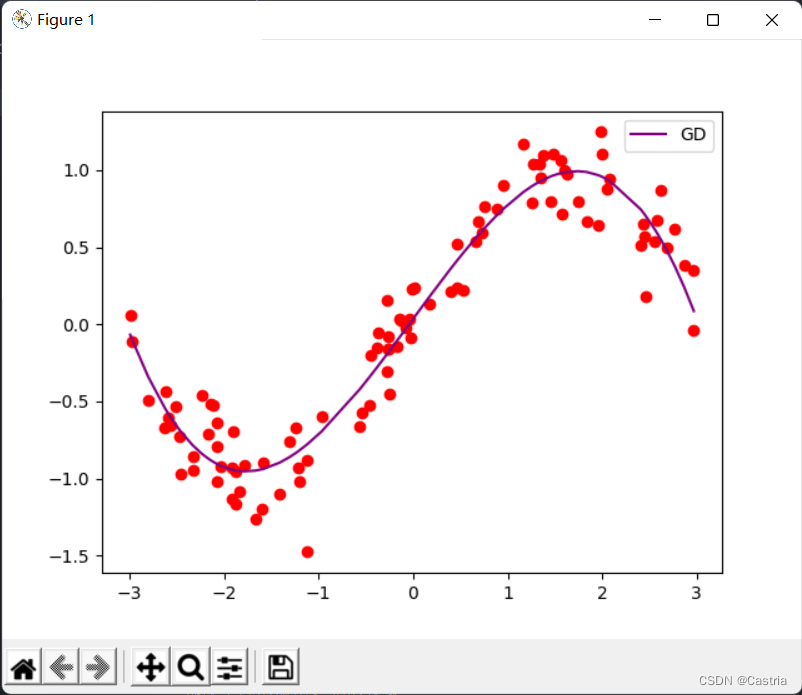
共役勾配法

共役勾配は、フォームA x = b A\pmb x=\pmb bを解くために使用できます。$あバツバツ=bb$の連立方程式$f(バツ\times )=\frac{}{2}{バツバツ}^{TA}\_バツバツ-{bb}^Tバツバツ+c.$ (正定$A$、2つは同等です)$A$は正定行列です。この問題では、$${バツ}^T\times W={よ}^{T}X、$$
次に${あ}_{(m+1)\times (m+1}={バツ}^{T}X、bb={よ}^T.$正則項を追加したい場合、それは解
$$(X^{T}X+\lambda E)W={よ}^{T}X.$$
まず、説明させてください:${バツ}^{T}X$は必ずしも正定値ではありませんが、半正定値でなければなりません (参照)。しかし、実験では基本的にこの問題を心配する必要はありません${バツ}^{T}X$は正定である可能性が非常に高く、コードにアサーションを追加するだけで、この条件にはあまり注意を払いません。
共役勾配法のアイデアと証明プロセスは比較的長いです.このシリーズ. ここではアルゴリズムの手順のみを示します (上記でリンクされた 3 番目の記事の冒頭):

(0) 初期化${バツ}_{(0};$
(1) 初期化$d_{(0}=r_{(0}=b-A{\times }_{(0};$
（2）令$$a_{(i}=\frac{r_{\left(i\right)}^{}{r}_{(i}}{d_{\left(i\right)}^{}アド\_{}_{(i}};$$
（3）迭代${バツ}_{(i+1}={バツ}_{(i}+a_{(i}{d}_{(i};$
（4）令$r_{(i+1}=r_{(i}-a_{(i}アド\_{}_{(i};$
（5）令$$b_{(i+1}=\frac{r_{(私+1)}^{}{r}_{(i+1}}{r_{\left(i\right)}^{}{r}_{(i}}、d_{(i+1}=r_{(i+1}+b_{(i+1}{d}_{(i}.$$
（6）当$\frac{||r_{(i}}{||r_{(0}||}<ϵ$の場合、アルゴリズムを停止します; そうでない場合は、(2) からの反復を続けます。$ϵ$は小さいプリセット値で、ここでは$10^{-5.}以下では、このプロセスに従ってコードを$
実装します。

'''
共轭梯度法(Conjugate Gradients, CG)求优化解, m 为多项式次数
- dataset 数据集
- m 多项式次数, 默认为 5
- regularize 正则化参数, 若为 0 则不进行正则化
'''
def CG(dataset, m = 5, regularize = 0):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    A = np.dot(X.T, X) + regularize * np.eye(m + 1)
    assert np.all(np.linalg.eigvals(A) > 0), '矩阵不满足正定!'
    b = np.dot(X.T, dataset[:, 1])
    w = np.random.rand(m + 1)
    epsilon = 1e-5

    # 初始化参数
    d = r = b - np.dot(A, w)
    r0 = r
    while True:
        alpha = np.dot(r.T, r) / np.dot(np.dot(d, A), d)
        w += alpha * d
        new_r = r - alpha * np.dot(A, d)
        beta = np.dot(new_r.T, new_r) / np.dot(r.T, r)
        d = beta * d + new_r
        r = new_r
        # 基本收敛，停止迭代
        if np.linalg.norm(r) / np.linalg.norm(r0) < epsilon:
            break
    return w

単純な勾配降下法と比較して、共役勾配法は迅速かつ安定して収束します。ただし、多項式の次数が増加するにつれて、適合は悪化します: $メートル=図7$を最小二乗法と比較すると、次のようになり

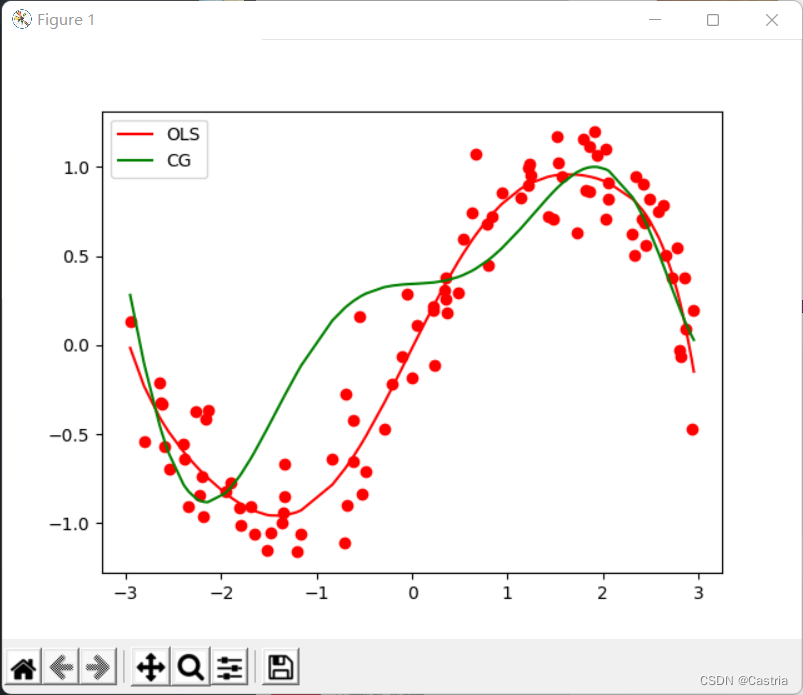
ます$メートル=7,l=1$ ):

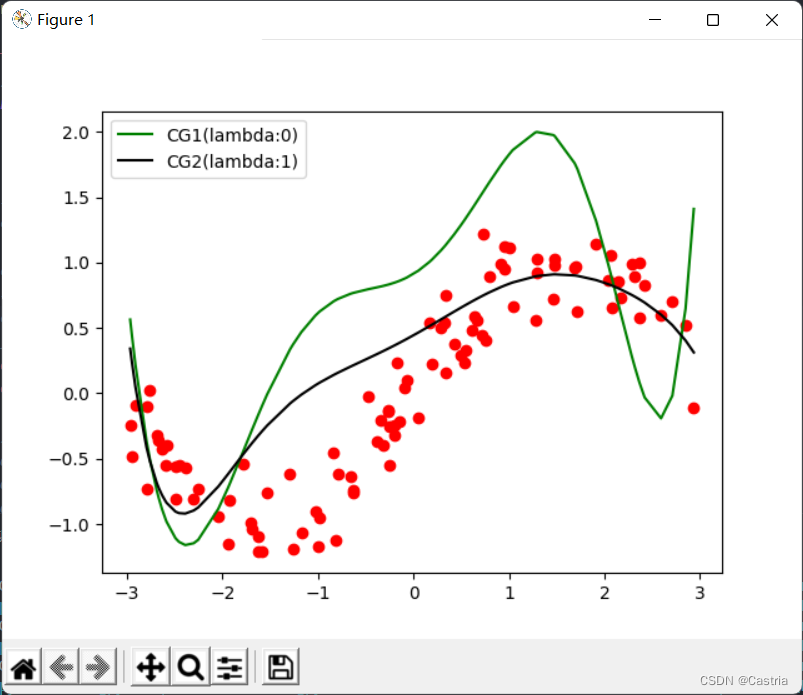
最後に、4 つの方法 (基本的には同じ) のフィッティング画像とメイン関数が添付され、実験要件に従ってパラメーターを調整できます。

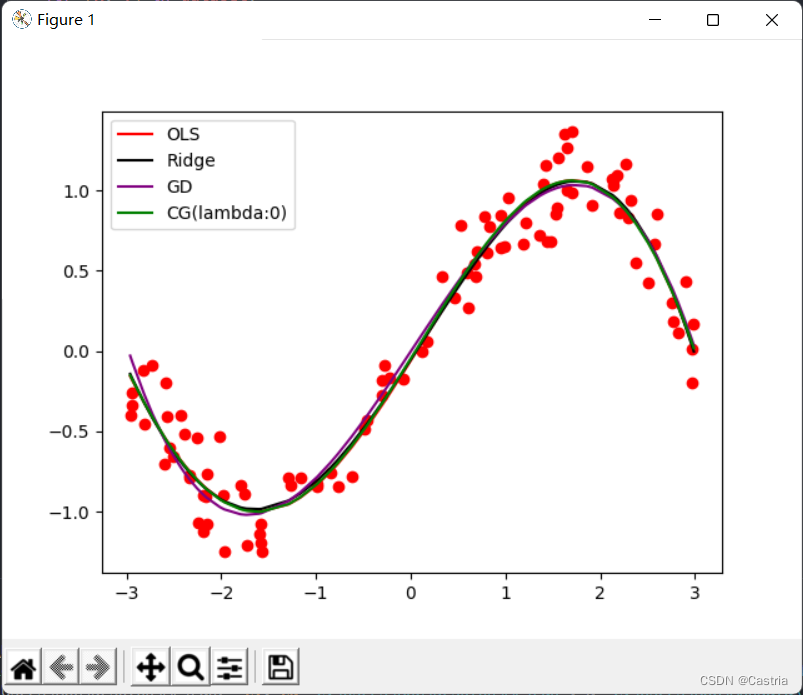
if __name__ == '__main__':
    warnings.simplefilter('error')

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    
    # 最小二乘法
    coef1 = fit(dataset)
    # 岭回归
    coef2 = ridge_regression(dataset)
    # 梯度下降法
    coef3 = GD(dataset, m = 3)
    # 共轭梯度法
    coef4 = CG(dataset)
    
    # 绘制出四种方法的曲线
    draw(dataset, coef1, color = 'red', label = 'OLS')
    draw(dataset, coef2, color = 'black', label = 'Ridge')
    draw(dataset, coef3, color = 'purple', label = 'GD')
    draw(dataset, coef4, color = 'green', label = 'CG(lambda:0)')

    # 绘制标签, 显示图像
    plt.legend()
    plt.show()