ターゲット検出モデルの評価指標とコード実装の詳細な説明

要約: モデルの汎化能力、つまりモデルの良し悪しを判断するためには、それを測定するための特定の指標を使用する必要があります.評価指標を使用すると、モデルの長所と短所を比較できます.このインデックスを使用して、モデルをさらに最適化します。

この記事は、Huawei クラウド コミュニティ「ターゲット検出モデルの評価指標とコード実装の詳細な説明」、著者: Embedded Vision から共有されています。

序文

モデルの一般化能力、つまりモデルの良し悪しを判断するには、特定の指標を使用してそれを測定する必要があります.評価指標を使用すると、さまざまなモデルの長所と短所を比較できます. 、このインデックスを使用してモデルをさらに最適化します。分類と回帰の 2 種類の教師ありモデルには、個別の評価基準があります。

問題やデータセットが異なれば、分類問題などのモデル評価指標も異なります.バランスの取れたデータセットカテゴリの場合、精度を評価指標として使用できますが、実際には、ほとんどすべてのデータセットがアンバランスなカテゴリであるため、一般的に、APは分類の評価指標として使用され、各カテゴリのAPが個別に計算され、次にmAPが計算されます。

1. 適合率、再現率、F1

1.1、正解率

Accuracy (precision) – Accuracy は、サンプル全体で予測された正しい結果のパーセンテージであり、次のように定義されます。

精度 = ( TP + TN )/( TP + TN + FP + FN )

エラー率と精度は一般的に使用されていますが、すべてのタスク要件を満たしているわけではありません。スイカの問題を例に取ります. メロン農家がスイカのカートを持ってきたと仮定すると, 訓練されたモデルを使用してスイカを識別します. 精度は、正しいカテゴリ (2 つのカテゴリ:良いメロンと悪いメロン) ). しかし、「収穫されたスイカのどのくらいの割合が良いメロンであるか」、または「すべての良いメロンのうちどれだけの割合が収穫されたか」にもっと関心がある場合、精度とエラー率の指標は明らかに十分ではありません.

正解率は全体の正解率を判断することはできますが、サンプルが偏っている場合は結果を測る良い指標にはなりません。簡単な例を挙げると、たとえば、サンプル全体では、ポジティブ サンプルが 90%、ネガティブ サンプルが 10% と、サンプルの偏りが深刻です。この場合、すべてのサンプルを陽性サンプルとして予測するだけで 90% の高い精度を得ることができますが、実際には、慎重に分類したわけではなく、何気なく分類しただけです。これは、サンプルの偏りの問題により、得られた高精度の結果には多くの水が含まれていることを示しています。つまり、サンプルのバランスが取れていない場合、正解率は無効になります。

1.2、適合率、再現率

適合率 (precision rate) P と再現率 (recall rate) R の計算には、混同行列の定義が含まれます。混同行列の表は次のとおりです。

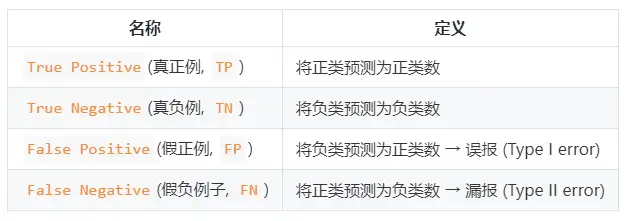
適合率と再現率の式:

• 精度率（精度率） P=TP/(TP+FP) P = TP /( TP + FP )
• 再現率（再現率） R=TP/(TP+FN) R = TP /( TP + FN )

精度率と精度率は似ていますが、まったく異なる概念です。精度率はポジティブ サンプルの結果の予測精度を表し、精度率はポジティブ サンプルとネガティブ サンプルの両方を含む全体的な予測精度を表します。

適合率は、モデルの正確さ、つまり、予測された正のサンプルのうちのいくつが真のサンプルであるかを示します。再現率は、モデルの完成度、つまり、モデルによって予測された真のサンプルの数を示します。ポジティブな例。適合率と再現率の違いは、分母の違いにあります. 1 つの分母は、陽性であると予測されるサンプルの数であり、もう 1 つは、元のサンプル内のすべての陽性サンプルの数です。

1.3、F1スコア

PとRのバランスを見つけたい場合は、新しい指標であるF 1 スコアが必要です。F 1 スコアは、適合率と再現率の両方を考慮して、2 つが同時に最高に達するようにバランスを取ります。F 1 の計算式は次のとおりです。    

ここでのF 1 の計算は二項分類モデル用です。多分類タスクのF 1 の計算については、以下を参照してください。  

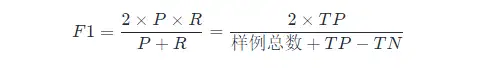
F 1 メトリクスの一般的な形式: Fβ。適合率/再現率に対するバイアスを表すことができます。Fβ は次のように計算されます。

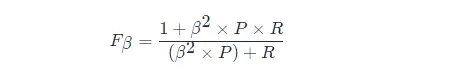
その中で、β > 1 は再現率への影響が大きく、β < 1 は適合率への影響が大きくなります。

コンピュータ ビジョンの問題が異なれば、2 種類のエラーの好みも異なり、特定の種類のエラーが特定のしきい値を超えない場合は、他の種類のエラーを減らそうとすることがよくあります。ターゲット検出では、mAP (平均平均精度) は両方のエラーを統一された指標として考慮します。

多くの場合、混同行列を取得できるたびに、複数のトレーニング/テストなど、複数の混同行列を使用するか、アルゴリズムの「グローバルな」パフォーマンスを推定することを期待して、複数のデータ セットでトレーニング/テストを行います。多分類タスクでは、 2 つのカテゴリの各組み合わせが混同行列に対応します; ...一般に、n n 個の 2 カテゴリ混同行列の適合率と再現率を総合的に検討したいと考えています 。

直接的なアプローチは、最初に各混同行列の適合率と再現率を計算することです。これらは ( P 1 , R 1 ), ( P 2 , R 2 ),...,( Pn , Rnとして記録されます。) 次に平均を取ると、「Macro Precision (Macro-P)」、「Macro Precision (Macro-R)」、および対応する「Macro F1 F 1 (Macro- F1 )」が得られます。

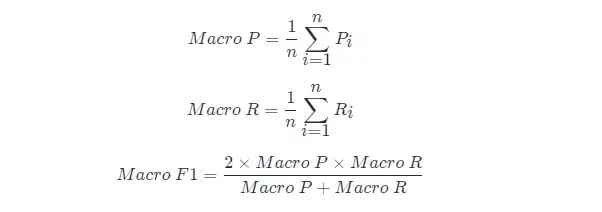
別の方法は、各混同行列の対応する要素を平均して TP、FP、TN、FN TP 、 FP 、 TN 、およびFNの平均値を取得し、「 マイクロ精度率」を計算することです (Micro-P ）、「マイクロリコール」（マイクロR）、「マイクロF1」（マイロF1） 

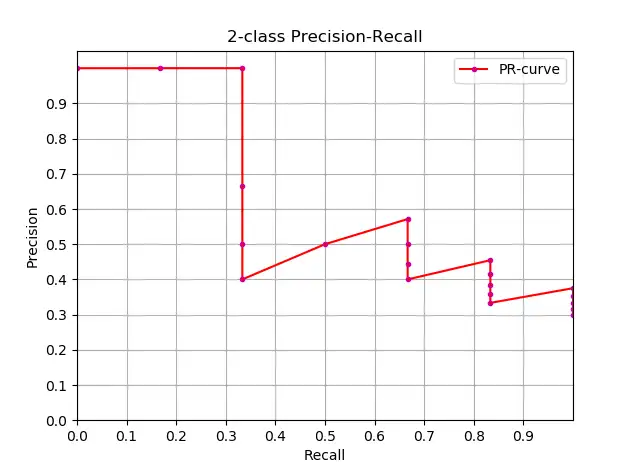
1.4、PR曲線

適合率と再現率の関係はPRグラフで表すことができます.適合率Pを縦軸に再現率Rを横軸にとると,適合率-再現率曲線が得られます. PR曲線として. PR 曲線の下の領域は AP として定義されます。  

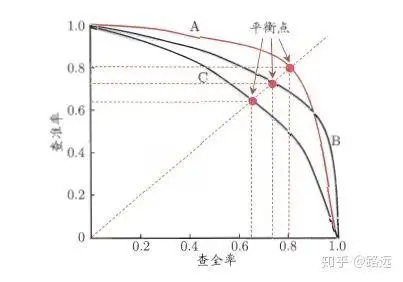
1.4.1、PR曲線の見方

ランキングモデルや分類モデルから理解できます。ロジスティック回帰を例にとると、ロジスティック回帰の出力は 0 と 1 の間の確率数です。したがって、この確率に従ってユーザーが良いか悪いかを判断したい場合は、しきい値を定義する必要があります。一般的に言えば、ロジスティック回帰の確率が高いほど 1 に近くなり、悪いユーザーである可能性が高くなります。たとえば、0.5 のしきい値を定義します。つまり、確率が 0.5 未満のすべてのユーザーを良いユーザーと見なし、確率が 0.5 を超えるユーザーを悪いユーザーと見なします。したがって、しきい値が 0.5 の場合、対応する適合率と再現率のペアを取得できます。

しかし、問題は、このしきい値が私たちによって恣意的に定義されており、このしきい値が要件を満たしているかどうかわからないことです。したがって、要件を満たす最適なしきい値を見つけるには、0 と 1 の間のすべてのしきい値をトラバースする必要があり、各しきい値は適合率と再現率のペアに対応するため、PR 曲線が得られます。

最後に、最適なしきい値ポイントを見つける方法は? まず、これら 2 つの指標の要件を説明する必要があります。適合率と再現率の両方が同時に非常に高いことを願っています。しかし実際には、この 2 つの指標は相反するものであり、2 倍の高値を達成することは不可能です。グラフから、一方が非常に高い場合、もう一方は非常に低いに違いないことが明らかです。適切なしきい値ポイントの選択は、実際のニーズに依存します. たとえば、高い再現率が必要な場合は、精度率を犠牲にします. 高い再現率を確保する場合、精度率はそれほど低くありません. .

1.5、ROC曲線とAUC面積

• PR曲線は横軸にRecall、縦軸にPrecisionをとり、ROC曲線は横軸にFPR、縦軸にTPRをとります**。PR 曲線が右上隅に近いほど、パフォーマンスが向上します。PR曲線の両方の指標は、ポジティブな例に焦点を当てています
• PR 曲線は Precision vs Recall 曲線を示し、ROC 曲線は FPR (x 軸: 偽陽性率) vs TPR (真陽性率、TPR) 曲線を示します。

1. [ ] ROC曲線
2. [ ] AUCエリア

2.APとmAP

2.1、AP および mAP 指標の理解

AP は各カテゴリのトレーニング済みモデルの品質を測定し、mAP はすべてのカテゴリのモデルの品質を測定します. AP を取得した後、mAP の計算は非常に単純になり、すべての AP の平均を取ることになります. APの計算式は比較的複雑なので（別章）、詳しくは以下を参照してください。

mAP という用語にはさまざまな定義があります。このメトリックは、情報検索、画像分類、およびオブジェクト検出の分野で一般的に使用されます。ただし、2 つのフィールドは異なる方法で mAP を計算します。ここでは、オブジェクト検出における mAP 計算方法についてのみ説明します。

mAP はターゲット検出アルゴリズムの評価指標としてよく使用されます. 具体的には, 各画像検出モデルが複数の予測フレームを出力する (実際のフレーム数をはるかに超える) ため, IoU (Intersection Over Union) を使用して、マークの予測は正確です。マーキングが完了した後, 再現率 R は予測フレームの増加とともに常に増加します. 正解率P は、異なる再現率 R レベルで平均化されて AP を取得し、最後にすべてのカテゴリがその比率に従って平均化されます.つまり、mAP インデックスが取得されます。

2.2、APの概算

AP の定義を知っている, 次のステップは、AP 計算の実現を理解することです. 理論的には, AP は積分によって計算できます. 式は次のとおりです:

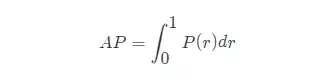
しかし、通常、 APの計算には近似法または補間法が使用されます。 

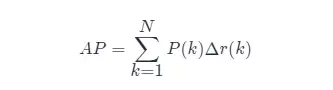
• APの近似計算(近似平均精度)、この計算方法は近似形式です。  
• 明らかに、垂直線上にあるポイントはAP の計算には寄与しません。  
• ここで、Nはデータの総量、kは各サンプル ポイントのインデックス、Δ r ( k ) = r ( k )− r ( k −1) です。   

AP の近似計算 と PR 曲線の描画のコードは次のとおりです。

import numpy as np
import matplotlib.pyplot as plt
class_names = ["car", "pedestrians", "bicycle"]
def draw_PR_curve(predict_scores, eval_labels, name, cls_idx=1):
 """calculate AP and draw PR curve, there are 3 types
    Parameters:
    @all_scores: single test dataset predict scores array, (-1, 3)
    @all_labels: single test dataset predict label array, (-1, 3)
    @cls_idx: the serial number of the AP to be calculated, example: 0,1,2,3...
    """
 # print('sklearn Macro-F1-Score:', f1_score(predict_scores, eval_labels, average='macro'))
 global class_names
    fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 10))
 # Rank the predicted scores from large to small, extract their corresponding index(index number), and generate an array
 idx = predict_scores[:, cls_idx].argsort()[::-1]
 eval_labels_descend = eval_labels[idx]
 pos_gt_num = np.sum(eval_labels == cls_idx) # number of all gt
 predict_results = np.ones_like(eval_labels)
 tp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend == cls_idx) # ndarray
 fp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend != cls_idx)
 tp_cum = np.cumsum(tp_arr).astype(float) # ndarray, Cumulative sum of array elements.
 fp_cum = np.cumsum(fp_arr).astype(float)
 precision_arr = tp_cum / (tp_cum + fp_cum) # ndarray
 recall_arr = tp_cum / pos_gt_num
    ap = 0.0
 prev_recall = 0
 for p, r in zip(precision_arr, recall_arr):
      ap += p * (r - prev_recall)
 # pdb.set_trace()
 prev_recall = r
 print("------%s, ap: %f-----" % (name, ap))
 fig_label = '[%s, %s] ap=%f' % (name, class_names[cls_idx], ap)
 ax.plot(recall_arr, precision_arr, label=fig_label)
 ax.legend(loc="lower left")
 ax.set_title("PR curve about class: %s" % (class_names[cls_idx]))
 ax.set(xticks=np.arange(0., 1, 0.05), yticks=np.arange(0., 1, 0.05))
 ax.set(xlabel="recall", ylabel="precision", xlim=[0, 1], ylim=[0, 1])
 fig.savefig("./pr-curve-%s.png" % class_names[cls_idx])
 plt.close(fig)

2.3、補間計算AP

内挿平均精度 AP APの式の進化過程についてはここでは説明しません. 詳細についてはこちらの記事を参照してください. ここにある式と図もこの記事を参照しています.  AP を計算する 11 点補間計算方法AP 式は次のとおりです。

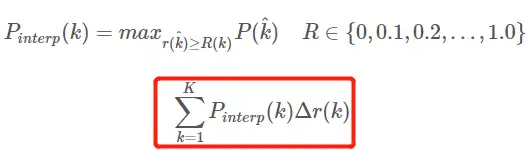
• これは、11 ポイントの通常の意味での AP です_補間形式、固定 0,0.1,0.2,…,1.00,0.1,0.2,…,1.0 11 のしきい値を選択、これは PASCAL2007 で使用されます
• ここでは、計算に含まれるポイントが 11 個しかないため、K = 11、11 points_Interpolated と呼ばれ、kはしきい値インデックスです。  
• Pinterp ( k )は、k 番目のしきい値に対応するサンプル ポイントの後のサンプルで最大値を取ります。中身。  

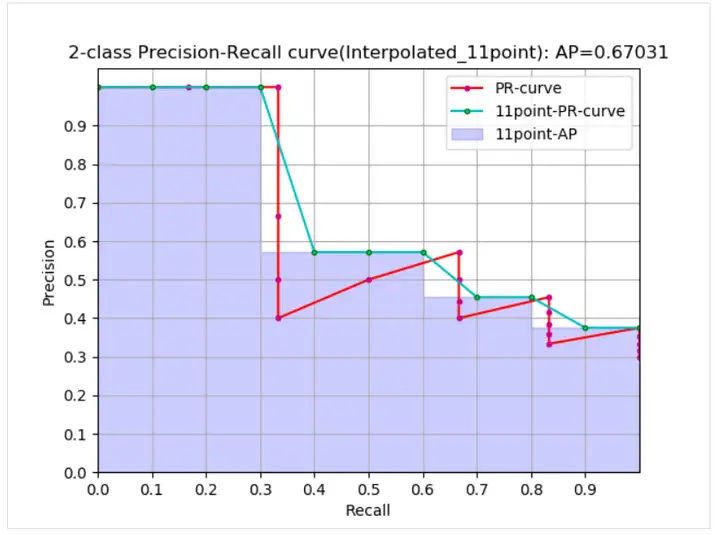
曲線から、実際の AP < 近似 AP < 補間 AP であり、11 点補間 AP は大きい場合も小さい場合もあり、データ量が多い場合は補間 AP に近くなります. 補間 AP とは異なり、AP は で計算されます.前の式. これは PR 曲線の面積推定値です. PASCAL 論文で与えられた式はより単純でより粗雑であり、11 のしきい値で精度の平均値を直接計算します. PASCAL 論文で与えられた AP を計算するための 11 点式は次のとおりです。

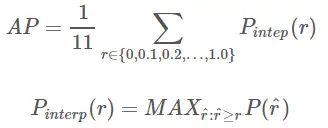
1. 特定の再現率と精度の条件下で AP を計算します。

def voc_ap(rec, prec, use_07_metric=False):
 """ 
    ap = voc_ap(rec, prec, [use_07_metric])
    Compute VOC AP given precision and recall.
    If use_07_metric is true, uses the
    VOC 07 11 point method (default:False).
    """
 if use_07_metric:
 # 11 point metric
        ap = 0.
 for t in np.arange(0., 1.1, 0.1):
 if np.sum(rec >= t) == 0:
                p = 0
 else:
                p = np.max(prec[rec >= t])
            ap = ap + p / 11.
 else:
 # correct AP calculation
 # first append sentinel values at the end
 mrec = np.concatenate(([0.], rec, [1.]))
 mpre = np.concatenate(([0.], prec, [0.]))
 # compute the precision envelope
 for i in range(mpre.size - 1, 0, -1):
 mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
 # to calculate area under PR curve, look for points
 # where X axis (recall) changes value
 i = np.where(mrec[1:] != mrec[:-1])[0]
 # and sum (\Delta recall) * prec
        ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
 return ap

2. AP 与えられたターゲット検出結果ファイルとテスト セット ラベル ファイル xml を計算します。

def parse_rec(filename):
 """ Parse a PASCAL VOC xml file 
 Return : list, element is dict.
    """
    tree = ET.parse(filename)
    objects = []
 for obj in tree.findall('object'):
 obj_struct = {}
 obj_struct['name'] = obj.find('name').text
 obj_struct['pose'] = obj.find('pose').text
 obj_struct['truncated'] = int(obj.find('truncated').text)
 obj_struct['difficult'] = int(obj.find('difficult').text)
 bbox = obj.find('bndbox')
 obj_struct['bbox'] = [int(bbox.find('xmin').text),
 int(bbox.find('ymin').text),
 int(bbox.find('xmax').text),
 int(bbox.find('ymax').text)]
 objects.append(obj_struct)
 return objects
def voc_eval(detpath,
 annopath,
 imagesetfile,
 classname,
 cachedir,
 ovthresh=0.5,
             use_07_metric=False):
 """rec, prec, ap = voc_eval(detpath,
 annopath,
 imagesetfile,
 classname,
                                [ovthresh],
                                [use_07_metric])
    Top level function that does the PASCAL VOC evaluation.
 detpath: Path to detections result file
 detpath.format(classname) should produce the detection results file.
 annopath: Path to annotations file
 annopath.format(imagename) should be the xml annotations file.
 imagesetfile: Text file containing the list of images, one image per line.
 classname: Category name (duh)
 cachedir: Directory for caching the annotations
    [ovthresh]: Overlap threshold (default = 0.5)
    [use_07_metric]: Whether to use VOC07's 11 point AP computation
        (default False)
    """
 # assumes detections are in detpath.format(classname)
 # assumes annotations are in annopath.format(imagename)
 # assumes imagesetfile is a text file with each line an image name
 # cachedir caches the annotations in a pickle file
 # first load gt
 if not os.path.isdir(cachedir):
 os.mkdir(cachedir)
 cachefile = os.path.join(cachedir, '%s_annots.pkl' % imagesetfile)
 # read list of images
 with open(imagesetfile, 'r') as f:
        lines = f.readlines()
 imagenames = [x.strip() for x in lines]
 if not os.path.isfile(cachefile):
 # load annotations
        recs = {}
 for i, imagename in enumerate(imagenames):
            recs[imagename] = parse_rec(annopath.format(imagename))
 if i % 100 == 0:
 print('Reading annotation for {:d}/{:d}'.format(
 i + 1, len(imagenames)))
 # save
 print('Saving cached annotations to {:s}'.format(cachefile))
 with open(cachefile, 'wb') as f:
 pickle.dump(recs, f)
 else:
 # load
 with open(cachefile, 'rb') as f:
 try:
                recs = pickle.load(f)
 except:
                recs = pickle.load(f, encoding='bytes')
 # extract gt objects for this class
 class_recs = {}
 npos = 0
 for imagename in imagenames:
        R = [obj for obj in recs[imagename] if obj['name'] == classname]
 bbox = np.array([x['bbox'] for x in R])
        difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
        det = [False] * len(R)
 npos = npos + sum(~difficult)
 class_recs[imagename] = {'bbox': bbox,
 'difficult': difficult,
 'det': det}
 # read dets
 detfile = detpath.format(classname)
 with open(detfile, 'r') as f:
        lines = f.readlines()
 splitlines = [x.strip().split(' ') for x in lines]
 image_ids = [x[0] for x in splitlines]
    confidence = np.array([float(x[1]) for x in splitlines])
    BB = np.array([[float(z) for z in x[2:]] for x in splitlines])
 nd = len(image_ids)
 tp = np.zeros(nd)
 fp = np.zeros(nd)
 if BB.shape[0] > 0:
 # sort by confidence
 sorted_ind = np.argsort(-confidence)
 sorted_scores = np.sort(-confidence)
        BB = BB[sorted_ind, :]
 image_ids = [image_ids[x] for x in sorted_ind]
 # go down dets and mark TPs and FPs
 for d in range(nd):
            R = class_recs[image_ids[d]]
            bb = BB[d, :].astype(float)
 ovmax = -np.inf
            BBGT = R['bbox'].astype(float)
 if BBGT.size > 0:
 # compute overlaps
 # intersection
 ixmin = np.maximum(BBGT[:, 0], bb[0])
 iymin = np.maximum(BBGT[:, 1], bb[1])
 ixmax = np.minimum(BBGT[:, 2], bb[2])
 iymax = np.minimum(BBGT[:, 3], bb[3])
 iw = np.maximum(ixmax - ixmin + 1., 0.)
 ih = np.maximum(iymax - iymin + 1., 0.)
                inters = iw * ih
 # union
 uni = ((bb[2] - bb[0] + 1.) * (bb[3] - bb[1] + 1.) +
 (BBGT[:, 2] - BBGT[:, 0] + 1.) *
 (BBGT[:, 3] - BBGT[:, 1] + 1.) - inters)
                overlaps = inters / uni
 ovmax = np.max(overlaps)
 jmax = np.argmax(overlaps)
 if ovmax > ovthresh:
 if not R['difficult'][jmax]:
 if not R['det'][jmax]:
 tp[d] = 1.
                        R['det'][jmax] = 1
 else:
 fp[d] = 1.
 else:
 fp[d] = 1.
 # compute precision recall
 fp = np.cumsum(fp)
 tp = np.cumsum(tp)
    rec = tp / float(npos)
 # avoid divide by zero in case the first detection matches a difficult
 # ground truth
 prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
    ap = voc_ap(rec, prec, use_07_metric)
 return rec, prec, ap

2.4、mAP計算方法

mAP値の計算は、データ セット内のすべてのカテゴリのAP値を平均することであるため、 mAPを計算するには、まず特定のカテゴリのAP値を見つける方法を知る必要があります。異なるデータ セットの特定のカテゴリのAP計算方法は類似しており、主に 3 つのタイプに分けられます。         

(1) VOC2007 では、Recall>=0,0.1,0.2,...,1 Recall >=0,0.1,0.2,...,1の場合、Precision の最大値を選択するだけで、合計 11 になります。 AP AP は これら 11 の精度の平均であり、mAP mAP はすべてのカテゴリのすべての AP AP 値の平均です。VOC データセットでAP APを計算するためのコード(補間計算方法を使用して、コードはpy-faster-rcnn ウェアハウスから取得されます)  

(2) VOC2010 以降では、異なる Recall 値 (0 と 1 を含む) ごとに、これらの Recall 値以上の場合の Precision の最大値を選択し、PR の下の面積を計算する必要があります。 AP 値としての曲線、mAP mAP はすべてカテゴリAP値の平均です。     

(3) COCO データセットに対して、複数の IOU しきい値 (0.5-0.95、0.05 はステップ サイズ) を設定し、各 IOU しきい値の下に AP 値の特定のカテゴリがあり、異なる IOU しきい値の下で AP 平均を計算します。つまり、カテゴリーの望ましい最終 AP 値です。

3. ターゲット検出メトリクスのまとめ

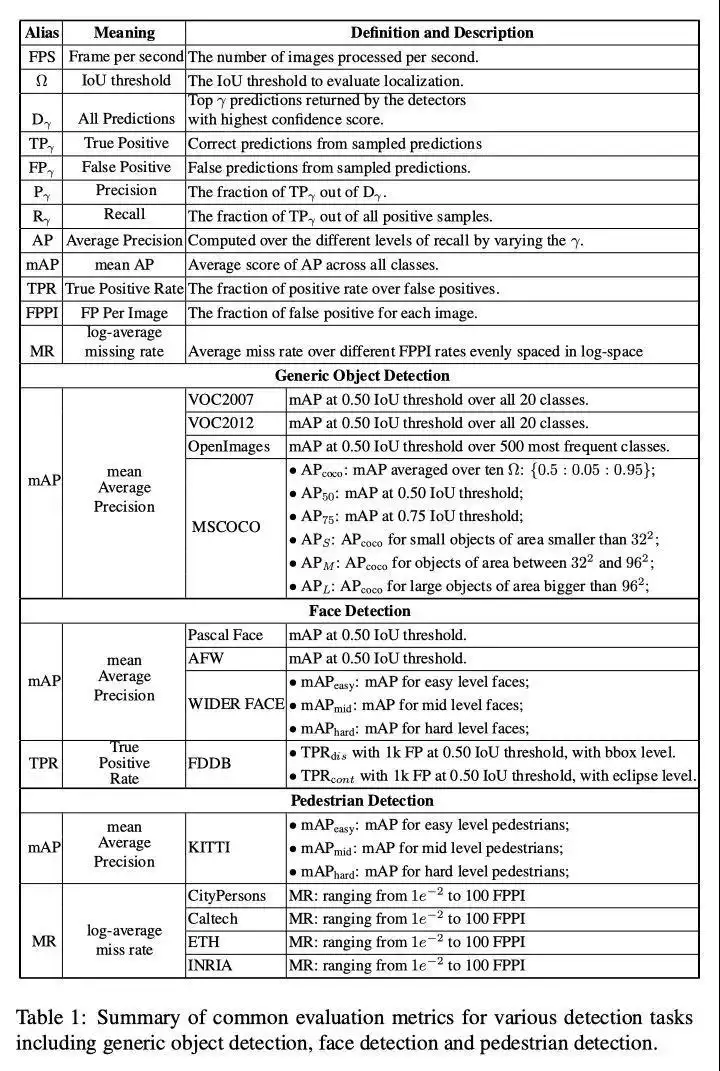
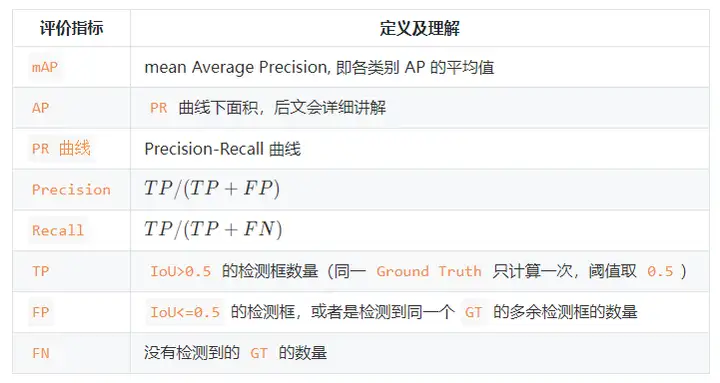
第四に、参考資料

• ターゲット検出評価基準-AP mAP
• 物体検出の性能評価指標
• ソフトNMS
• 物体検出のための深層学習の最近の進歩
• より高速な R-CNN のシンプルで高速な実装
• 分類モデルの評価指標 - 正解率、適合率、再現率、F1、ROC 曲線、AUC 曲線
• この記事では、精度、適合率、再現率、真率、偽陽性率、ROC/AUC を完全に理解できます。

 

クリックしてフォローし、Huawei Cloudの新しいテクノロジーについて初めて学びましょう〜

{{o.name}}

{{m.name}}