ニューラルネットワークにおけるバックプロパゲーションと勾配降下の詳細な説明

要約: バックプロパゲーションは、ニューラルネットワークのパラメーターの勾配を計算する方法を指します。

この記事は、Huawei クラウドコミュニティ「バックプロパゲーションと勾配降下の詳細な説明」、著者: Embedded Vision から共有されています。

1. 順伝播と逆伝播

1.1、ニューラルネットワークのトレーニングプロセス

ニューラルネットワークのトレーニングプロセスは次のとおりです。

最初に、ランダムなパラメーターを介して結果 (モデルの順伝播プロセス) を「推測」します。これは、ここでは予測結果と呼ばれます。
次に、aとサンプルラベル値 y の間のギャップを計算します (つまり、損失関数の計算プロセス)。
次に、バックプロパゲーションアルゴリズムを介してニューロンのパラメーターを更新し、新しいパラメーターで再試行します. 今回は "推測" ではなく、根拠を持って正しい方向に近づいています. 結局、パラメーターの調整は戦略的です (に基づいて)勾配ドロップ戦略)。

予測結果と実際の結果の差がほとんどなくなるまで、つまり |a−y|→0 になるまで、上記の手順を何度も繰り返して、トレーニングを終了します。

1.2、順伝播

順伝播 (またはフォワードパス) とは、ニューラルネットワークの各層の結果を順番に (入力層から出力層まで) 計算して格納することを指します。

順伝播の計算プロセスをよりよく理解するために、ネットワーク構造に従ってネットワークの順伝播計算図を描くことができます。次の図は、単純なネットワークとそれに対応する計算グラフの例です。

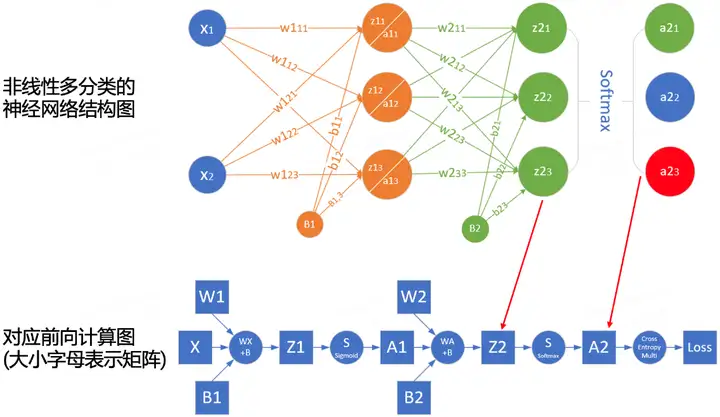
四角は変数を表し、丸は演算子を表します。データフローの方向は、左から右に順番に計算されます。

1.3、逆伝播

バックプロパゲーション (バックワードプロパゲーション、BP と呼ばれる) は、ニューラルネットワークパラメーターの勾配を計算する方法を指します。その原理は、微積分の連鎖律に基づいており、出力層から入力層までネットワークを逆順にたどり、各中間変数とパラメーターの勾配を順番に計算します。

勾配の自動計算 (自動微分) により、ディープラーニングアルゴリズムの実装が大幅に簡素化されます。

バックプロパゲーションアルゴリズムは、計算の繰り返しを避けるために、フォワードプロパゲーションに保存された中間値を再利用することに注意してください. したがって、フォワードプロパゲーションの中間結果を保存する必要があり、これにより、モデルのトレーニングに純粋な予測よりも多くのメモリが必要になります。（ビデオメモリ）。同時に、これらの中間結果が占有するメモリ (ビデオメモリ) のサイズは、ネットワーク層の数とバッチサイズ (batch_size) に比例するため、大きな batch_size を使用してより深いネットワークをトレーニングすると、アウトが発生する可能性が高くなります。メモリ (メモリ不足) エラー!

1.4、まとめ

順伝播は、中間変数を計算し、ニューラルネットワークによって定義された計算グラフに、入力層から出力層まで順番に格納します。
バックプロパゲーションは、ニューラルネットワークの中間変数とパラメーターの勾配を逆の順序 (出力層から入力層へ) で計算して格納します。
ニューラルネットワークをトレーニングする場合、モデルパラメーターを初期化した後、確率的勾配降下最適化アルゴリズム (または Adam などの他の最適化アルゴリズム) と組み合わせて、バックプロパゲーションによって計算された勾配に基づいて、フォワードプロパゲーションとバックプロパゲーションを交互に使用してモデルパラメーターを更新します。 .
ディープラーニングモデルのトレーニングには、予測よりも多くのメモリが必要です。

第二に、勾配降下法

2.1、深層学習における最適化

ほとんどの深層学習アルゴリズムには、何らかの形の最適化が含まれます。オプティマイザーの目的は、損失面で損失値の最小点にスムーズに到達できるように、ネットワークの重みパラメーターを更新することです。

深層学習の最適化には多くの課題があります。最も煩わしいのは、極小値、鞍点、および消失勾配です。

極小値: 任意の目的関数 f(x) について、x での f(x) の対応する値がx小さい場合、 f(x) は極小値である可能性があります。xでの f(x) の値が領域全体にわたる目的関数の最小値である場合、f ( x ) は大域的最小値です。
鞍点: 関数のすべての勾配が消失するが、グローバル最小値でもローカル最小値でもない任意の位置を指します。
消失勾配: 何らかの理由で、目的関数f の勾配がゼロに近くなります (つまり、勾配消失問題)。これが、ReLU 活性化を導入する前に深層学習モデルをトレーニングすることが非常に難しい理由の 1 つです。関数と ResNet。

深層学習では、目的関数のほとんどが複雑で、解析解がないため、数値最適化アルゴリズムを使用する必要があり、この論文の最適化アルゴリズム: SGD と Adam はこのカテゴリに属します。

2.2、勾配降下法を理解する方法

勾配降下 (GD) アルゴリズムは、ニューラルネットワークモデルのトレーニングで最も一般的なオプティマイザーです。勾配降下法が深層学習で直接使用されることはめったにありませんが、それを理解することは、確率的勾配降下法とミニバッチ確率的勾配降下法アルゴリズムを理解するための基本です。

ほとんどの記事では、勾配降下法を理解するために「山に閉じ込められた人が谷の底にすばやく降りる必要がある」という例を使用していますが、これは完全に正確ではありません. 自然界では、勾配降下の最も良い例は、湧き水が丘を下っていくプロセスです。

水は重力の影響を受けて、現在の位置で最も急な方向に流れ、滝を形成することがあります (勾配の反対方向は、関数値が最も速く低下する方向です)。
山を下る水の経路は一様ではなく、同じ場所に同じ急勾配の場所が複数ある場合があり、それが分流の原因となります（複数の解が得られます）。
くぼみに遭遇すると、湖が形成され、下り坂のプロセスが終了します (グローバルな最適解は得られませんが、局所的な最適解は得られます)。

例は AI-EDU: Gradient Descent を参照してください。

2.3、勾配降下の原理

勾配降下の数式:

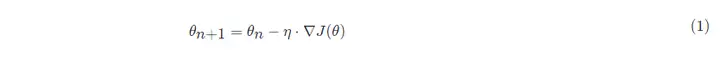
の：

θn+1 : 次の値 (ニューラルネットワーク内のパラメーターの更新された値);
θn : 現在の値 (現在のパラメーター値);
−: マイナス記号、勾配の逆方向 (勾配の逆方向は、関数値が最も速く減少する方向です)。
η: 学習率またはステップサイズ、各ステップで移動する距離を制御します。最高の景勝地を見逃すのを避けるために速すぎず、長時間を避けるために遅すぎないようにします (手動で調整する必要があるハイパーパラメーター)。
∇: 勾配、関数の現在の位置の最も速い上昇点 (勾配ベクトルは上り坂を指し、負の勾配ベクトルは下り坂を指します);
J(θ): 関数 (最適化されるのを待っている目的関数)。

下の図は、勾配降下法の手順を示しています。勾配降下法の目的は、x値を極値に近づけることです。

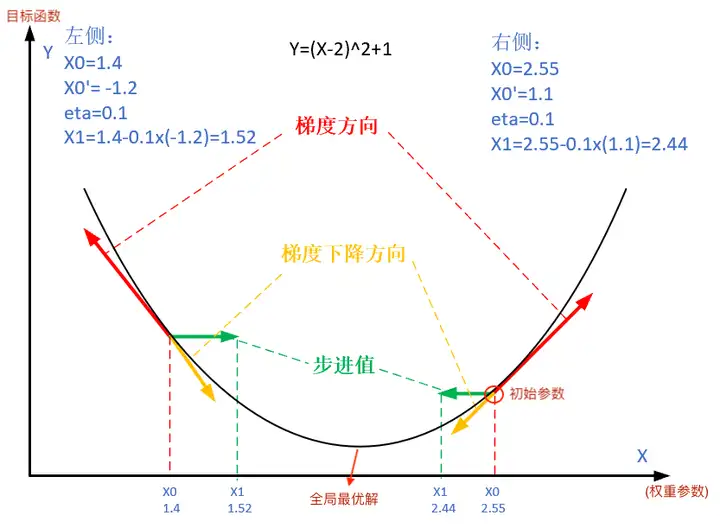
二変量であるため、勾配降下の反復プロセスは 3 次元プロットで説明する必要があります。表 2 は、勾配降下プロセスを 3D 空間で視覚化したものです。

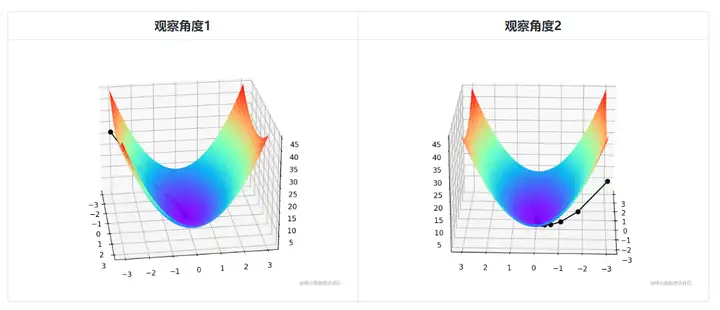
図の中央にあるかすかな黒い線は、赤い高地から坂道を下って青い窪みまでの勾配降下のプロセスを表しています。

二変量凸関数 J(x,y)=x2+2y2 の勾配降下最適化プロセスと可視化コードは次のとおりです。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def target_function(x,y):
    J = pow(x, 2) + 2*pow(y, 2)
 return J
def derivative_function(theta):
    x = theta[0]
    y = theta[1]
 return np.array([2*x, 4*y])
def show_3d_surface(x, y, z):
    fig = plt.figure()
    ax = Axes3D(fig)
    u = np.linspace(-3, 3, 100)
    v = np.linspace(-3, 3, 100)
    X, Y = np.meshgrid(u, v)
    R = np.zeros((len(u), len(v)))
 for i in range(len(u)):
 for j in range(len(v)):
 R[i, j] = pow(X[i, j], 2)+ 4*pow(Y[i, j], 2)
 ax.plot_surface(X, Y, R, cmap='rainbow')
 plt.plot(x, y, z, c='black', linewidth=1.5,  marker='o', linestyle='solid')
 plt.show()
if __name__ == '__main__':
    theta = np.array([-3, -3]) # 输入为双变量
    eta = 0.1 # 学习率
    error = 5e-3 # 迭代终止条件，目标函数值 < error
    X = []
    Y = []
    Z = []
 for i in range(50):
 print(theta)
        x = theta[0]
        y = theta[1]
        z = target_function(x,y)
 X.append(x)
 Y.append(y)
 Z.append(z)
 print("%d: x=%f, y=%f, z=%f" % (i,x,y,z))
 d_theta = derivative_function(theta)
 print("    ", d_theta)
        theta = theta - eta * d_theta
 if z < error:
 break
    show_3d_surface(X,Y,Z)

知らせ！要約すると、さまざまなステップサイズ η は、反復回数が増加するにつれて、最適化された関数 J の値にさまざまな変化をもたらします。

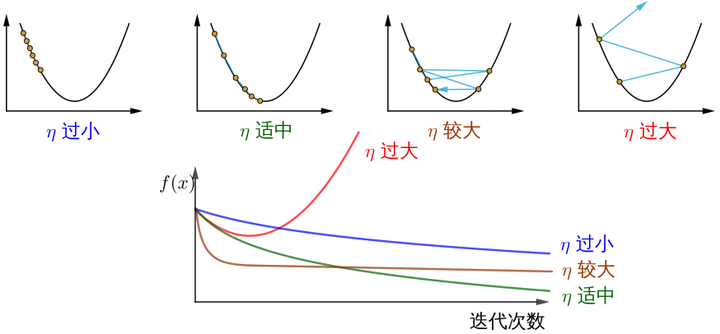
画像ソースは勾配降下法をどのように理解していますか? .

3、確率的勾配降下法と小バッチ確率的勾配降下法

3.1、確率的勾配降下

深層学習では、目的関数は通常、トレーニングデータセットの各サンプルの損失関数の平均です。勾配降下法を使用する場合、独立変数の反復ごとの計算コストは O(n) であり、n (サンプル数) に比例して増加します。したがって、トレーニングデータセットが大きい場合、反復ごとの勾配降下の計算コストが高くなります。

確率的勾配降下 (SGD) は、反復ごとの計算コストを削減します。確率的勾配降下法の各反復では、データサンプルをインデックス i (i ∈ 1,...,n) でランダムに一様にサンプリングし、勾配 ∇J(θ) を計算して重みパラメーター θ を更新します。

反復あたりの計算コストは、勾配降下の O(n) から定数 O(1) に低下します。また、確率的勾配 ∇J(θ) は完全な勾配 ∇J(θ) の偏りのない推定値であることも強調する価値があります。

偏りのない推定は、サンプル統計を使用して母集団パラメーターを推定する場合の偏りのない推論です。

実際のアプリケーションでは、確率的勾配降下 SGD 法を動的学習率法と組み合わせて使用する必要があります。そうしないと、固定学習率 + SGD の組み合わせにより、モデルの収束プロセスがより複雑になります。

3.2、ミニバッチ確率的勾配降下法

前述の勾配降下法 (GD) および確率的勾配降下法 (SGD) の方法は、完全なデータセットを使用して勾配を計算してパラメーターを更新するか、一度に 1 つのトレーニングサンプルのみを処理してパラメーターを更新するかのいずれかで、極端すぎます。実際のプロジェクトでは、この 2 つの妥協点、つまりミニバッチ勾配降下法が使用されますが、ミニバッチ勾配降下法を使用すると、計算効率も向上します。

ミニバッチのすべてのサンプルデータ要素はトレーニングセットからランダムに抽出され、サンプル数は batch_size (bs と省略) です。

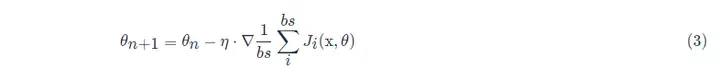
さらに、一般的なプロジェクトで使用される SGD 最適化アルゴリズムは、デフォルトで小さなバッチの確率的勾配降下を使用します。つまり、batch_size > 1 です。グラフィックカードのメモリが不十分でない限り、batch_size = 1 が設定されます。

参考文献

勾配降下法を理解するには？
AI-EDU: 勾配降下法
「ハンズオンディープラーニング第 11 章 - 最適化アルゴリズム」

クリックしてフォローし、Huawei Cloudの新しいテクノロジーについて初めて学びましょう〜