山の外の風雨の三尺剣
用事があるなら剣を持って山を下りなさい
雲の中の花と鳥の家 本
安心のパラパラ漫画の賢者がやってくる
1. 設定に関する質問
回帰を学ぶために、Web 広告とクリックの関係を例として取り上げます。
前提: 投資される広告料が多ければ多いほど、広告のクリック数も増加します。
過去の経験データによれば、次のような数値が得られます。

では、広告料として 200 元を投資するとします。どのくらいのクリック数が得られるでしょうか?
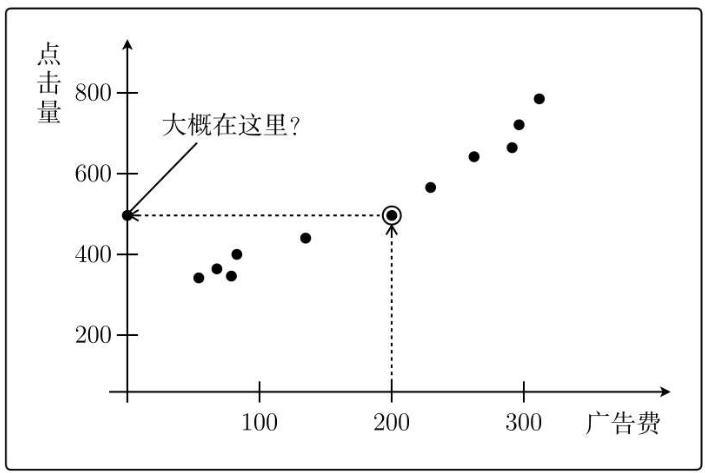
それは約500回です。
これが機械学習です。あなたがやっていることは、既知のデータから学習して予測を与えることです。
2. モデルを定義する
グラフの各点の関数形がわかれば、広告料に基づくクリック数を知ることができます。
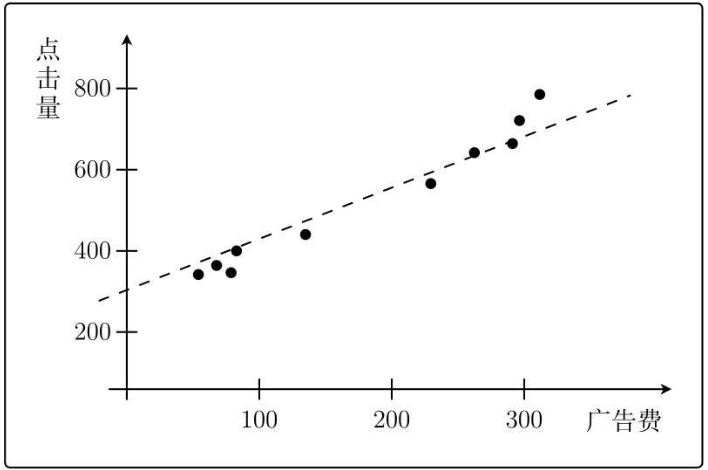
注: 「ヒットにはノイズが含まれる」ため、関数がすべてのポイントを通過することは不可能です。
関数を取得できます。
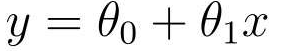
1 つは切片、もう 1 つは傾きです。
この関数から、x が広告料、y がクリック数であることがわかります。
上記の一次関数は、広告費の投資額に基づいてクリック数を予測できるモデルとして想像でき、θ0とθ1はそのモデルのパラメータ値です。モデルの品質 (つまり、予測結果の精度) は、モデルのパラメーター値と密接に関係しています。
現在、これら 2 つのパラメーターの値がいくつこのモデルに最適であるかはわかりません。
数学の仮説法によると、分からないからまずは適当に仮説を立ててみましょう。まず θ0=1、θ1=2 と仮定すると、上記の一次関数は次のようになります。

この仮説モデルによると、広告料金として x=100 元を投資し、予測されるクリック数は次のようになります。
y = 1 + 2 * 100 =201
前のデータの実際の状況を見てください。
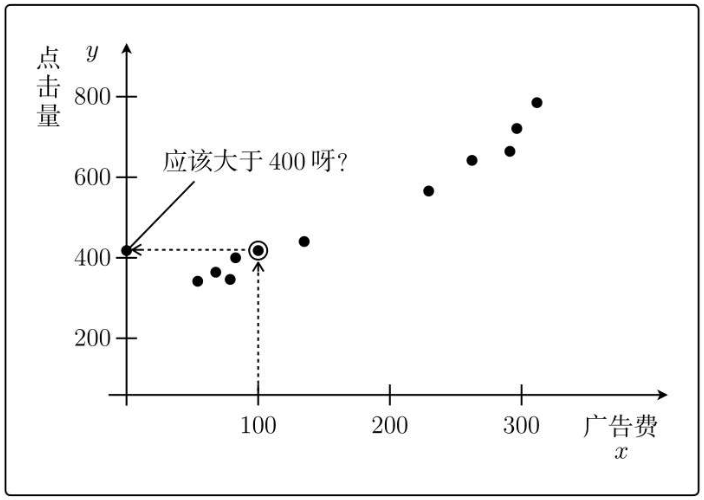
したがって、仮定した θ0=1 および θ1=2 は完全に誤りであり、これら 2 つのパラメータに基づいて得られたモデルは正しい結果を得ることができません。
次に、機械学習を使用して、正しい θ0 と θ1 を見つけます。
3 最小二乗法
まず、関数の式を 1 回変換します。
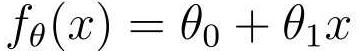
このように、パラメータθを持ち、変数xに関係する関数であることが一目でわかります。
以前、次のような広告費用とクリック数の間の実際のデータがありました。
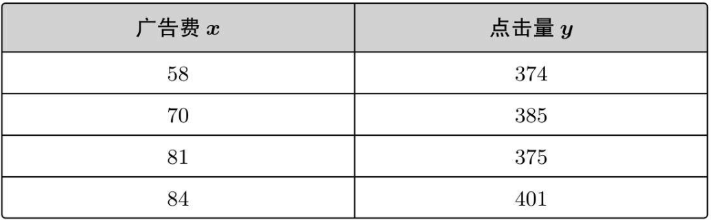
図で表すと次のようになります。

何気なく仮定したパラメータによると、fθ(x)=1+2x が得られます。
実際の広告コストを予測クリック数に代入します。
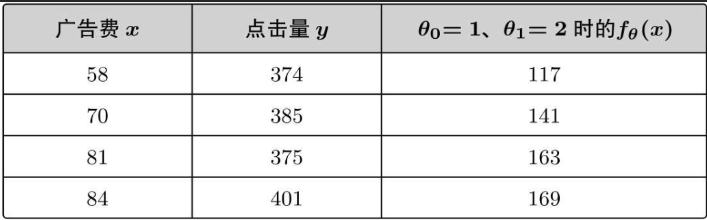
ランダムに仮定されたパラメータに基づく予測値は実際の状況とは大きく異なり、ランダムに決定されたパラメータを使用して計算された値と実際の値の間には偏差があることがわかります。
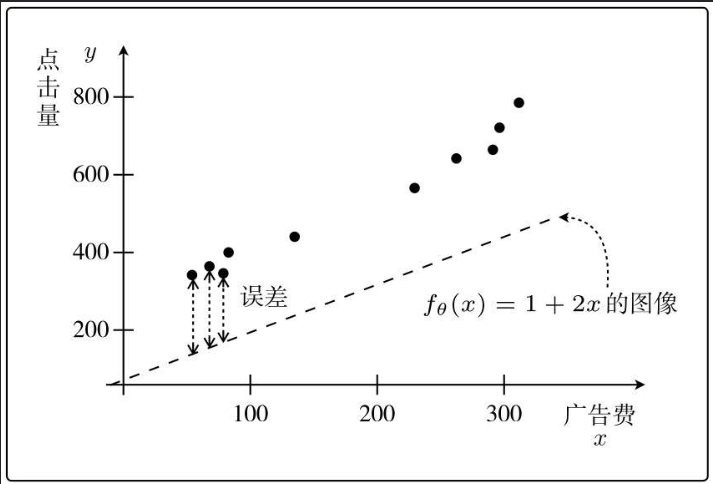
理想的には、予測値は実際の値、つまり y-fθ(x)=0 と一致します。これは、y と fθ(x) の間の誤差が 0 であることを意味します。
ただし、すべての誤差を 0 にすることは不可能なので、すべての点の誤差の合計をできるだけ小さくする必要があります。
式で表すと次のようになります。

この式を目的関数(コア)といい、E(θ)のEは英語のErrorの頭文字であり、このような問題を最適化問題といいます。
注意点:
1. x(i) と y(i) の i は i のべき乗を意味するものではなく、i 番目の学習データを指します。
2. 誤差の 2 乗を計算するには、誤差が負の場合を除外します。
3. 1/2 を掛けると、式はより適切に微分され、関数自体が最小値を取る点には影響しません。
初期広告料とクリック数データを代入すると、次の結果が得られます。
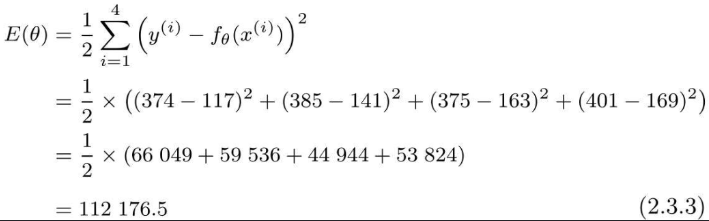
誤差が大きすぎる場合は、誤差を小さくして予測値が実際の値に近づくようにする必要があります。この誤差を求める方法は、最小二乗法とも呼ばれます。
E(θ)をどんどん小さくするには、パラメータθの値を保持し、実際の値と何度も比較・修正する必要があり、面倒なので微分を使うのが正しい方法です。
例:
g(x)=(x-1)*2 という二次関数があります。

まず g(x) を微分します。

その増減表を知ることができます。

x=3 で、g(x) の値を小さくするには、x を左に移動する必要があります。つまり、x を減らす必要があります。

反対側の x=-1 の点で、g(x) の値を小さくするには、x を右に移動する、つまり x を大きくする必要があります。
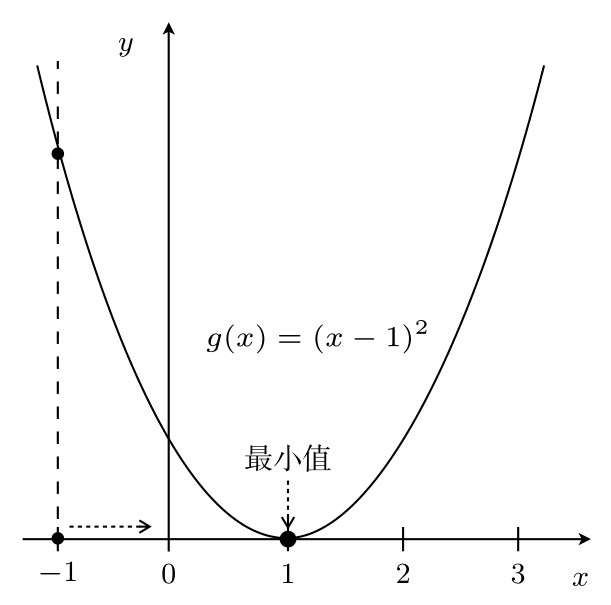
つまり、x の移動方向は微分値の符号に応じて決まり、微分値の符号と逆方向に移動する場合、g(x) は最小値の方向に進みます。
上記の内容を要約すると、次の式で表現できます。
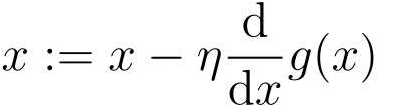
これは最急降下法または勾配降下法です。
A:=B この書き方は、A が B を通じて定義され、パラメータが自動的に更新されることを意味します。簡単に言えば、前の x は新しい x を定義するために使用されます。
η は学習率と呼ばれ、「イタ」と発音されます。学習率に応じて、最小値に達するまでの更新回数も異なります。つまり、収束速度が異なります。場合によっては、まったく収束できず、常に発散する状況さえあります。
したがって、x=3 から始まる η=1 など、η の値は非常に重要です。

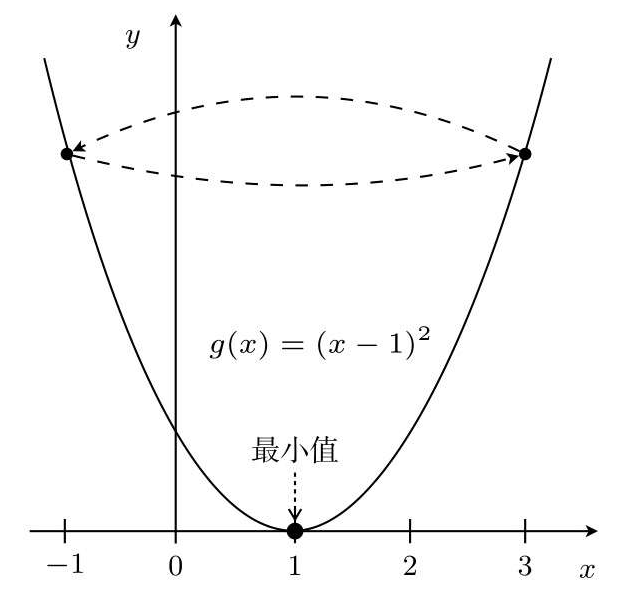
これは無限ループにつながります。
η=0.1 とし、同じく x=3 から開始します。


η が大きい場合、x:=x-η(2x-2) は 2 つの値を中心にジャンプし、場合によっては最小値から大きく外れることもあります。これがダイバージェント状態です。そしてηが小さいと移動量も小さいので更新回数は多くなりますが、確かに値は収束する方向に進みます。
ここで、広告コストとクリック数の目的関数について説明します。
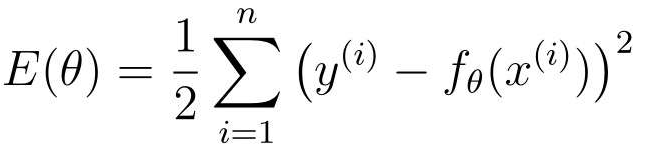
ただし、この目的関数には fθ(x) が含まれており、fθ(x) には 2 つのパラメータ θ0 と θ1 があります。つまり、この目的関数は θ0 と θ1 の二変量関数なので、常微分は使えず偏微分が使えます。
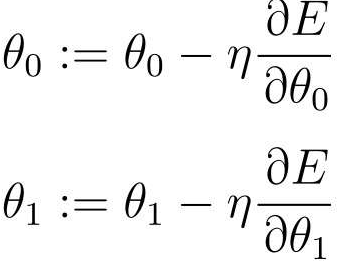
式 θ0 の偏微分を求めます。
E(θ)にはfθ(x)、fθ(x)にはθ0があるので複合関数が使えます
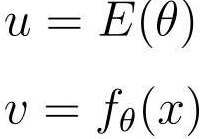
段階的に微分する
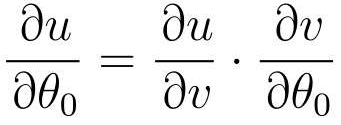
u と v を微分したところから計算を開始します。
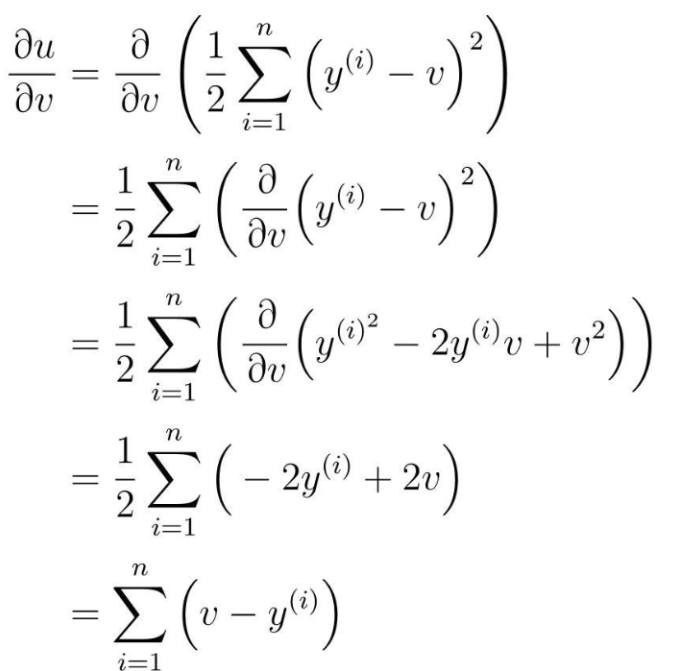
次に、v で θ0 を微分します。
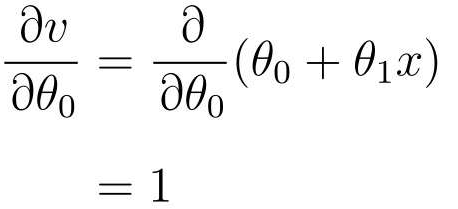
v は fθ(x) を元に戻します

次に、v で θ0 を微分します。
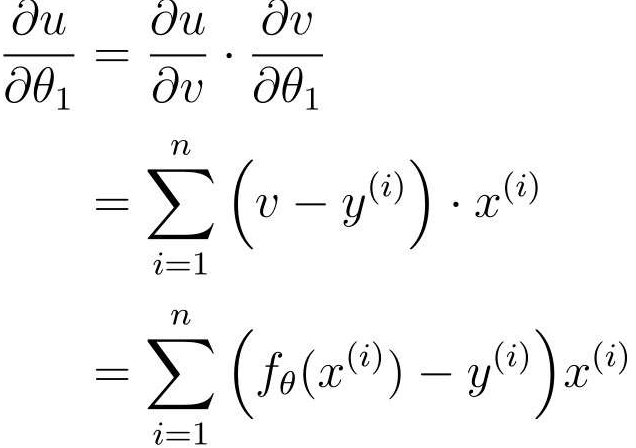
最後に、パラメータ θ0 と θ1 の更新式が得られます。

この式に従ってθ0とθ1を更新すれば正しい一次関数fθ(x)を求めることができます。
この方法を使用して正しい fθ(x) を見つけ、広告料金を入力して対応するクリック数を取得します。このようにして、広告費用に基づいてクリック数を予測できます。
4 多項式回帰
以前は、画像は直線にフィットしていましたが、実際には、直線よりも曲線の方がよくフィットします。

曲線に対応する二次関数:
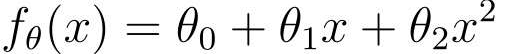
あるいは、より高次の表現も可能です。
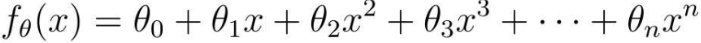
ただし、関数の次数が優れているほどフィッティングが向上するわけではなく、オーバーフィッティングの問題が発生する可能性があります。
最後のパラメータ更新式は次のとおりです。

このように関数内の多項式の次数を増やしてその関数を利用する解析方法を多項式回帰といいます。
5 重回帰
従来は広告料を基にクリック数を予測していましたが、変数は広告料 x の 1 つだけでしたが、実際には変数が 2 つ以上ある複雑な問題が多くなりました。
例えば、クリック数は、広告料金以外にも、広告の掲載位置や広告ページのサイズなどの複数の要因、すなわち複数の変数xの影響を受ける。
問題をできるだけ単純にするために、今回は広告ページのサイズだけを考えます。広告料を x1、広告欄の幅を x2、広告列の高さを x3 として、 fθ は次のように表すことができます。

その後、関数を微分することができますが、その前に、式の簡略化された形式を理解することができます。
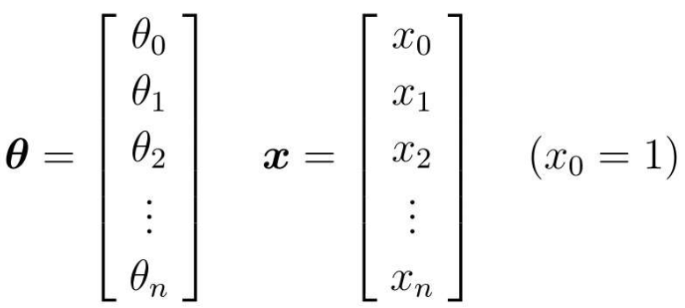
簡略化方法: パラメータ θ と変数 x をベクトルとして扱う

計算を容易にするために、両側を揃えます
θを転置し、xを掛けた結果
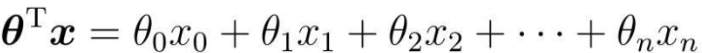
したがって、実際のプログラミングでは、通常の 1 次元配列で表現するだけで済みます。

微分は前と同じなので、v から θj までの微分だけが必要です。

次に、j 番目のパラメータの更新式は次のようになります。
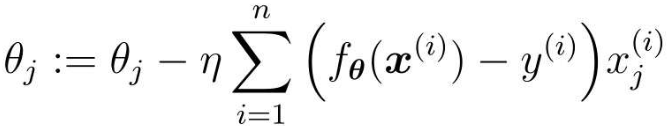
このような複数の変数を含む回帰は、重回帰と呼ばれます。
6 確率的勾配降下法
上記の勾配降下アルゴリズムには、x を何度も更新するのに時間がかかること、もう 1 つは局所最適解に陥りやすいという 2 つの欠点があります。
たとえば、次の関数:
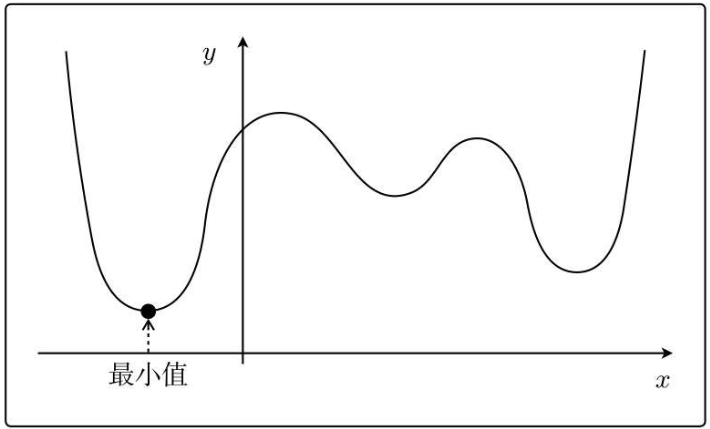
さまざまな場所から最初の x を選択すると、局所的な最適解が得られます。
確率的勾配降下法は、最急降下法に基づいています。
最急降下法のパラメータ更新式:
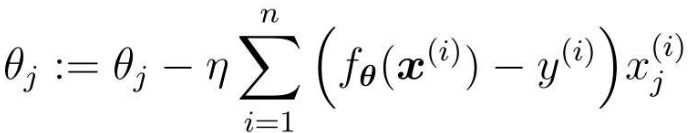
この式はすべてのトレーニング データの誤差を使用します。一方、確率的勾配降下法では、トレーニング データがランダムに選択され、パラメーターの更新に使用されます。

式内の k は、ランダムに選択されたデータのインデックスです。最急降下法ではパラメーターを 1 回更新するのにかかる時間、確率的勾配降下法では n 回更新できます。また、確率的勾配降下法は、学習データがランダムに選択され、パラメータ更新時に使用される勾配がデータ選択時の勾配となるため、目的関数の局所最適解に陥りにくい。
さらに、m 個のトレーニング データをランダムに選択してパラメータを更新する方法もあります。
ランダムに選択された m 個のトレーニング データのインデックス セットを K とします。
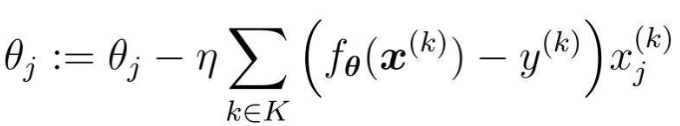
トレーニング データが 100 個あると仮定すると、m=10 の場合、10 個の乱数を含むインデックスのセットを作成します (例: K={61, 53, 59, 16, 30, 21, 85,31, 51, 10})。その後、ライン上のパラメータを繰り返し更新します。
この方法は、ミニバッチ勾配降下法と呼ばれます。