著者:ユー・ファン
背景
シュレディンガー方程式は量子力学の基本方程式であり、この方程式を解くことにより、ほとんどの物理的および化学的問題を解決できます。しかし、問題は、分子系の次元が増加するにつれて、シュレーディンガー方程式の基底関数の数が指数関数的に増加することです。たとえば、メタン分子には 5 つの原子があり、その次元は 9=3*5 – 6 であり、その数は次のようになります。基底関数は 10 の 9 乗です。
シュレーディンガー方程式は正確に解くことができないため、高精度の近似解を使用して分子の化学的性質を予測できます。コンフィギュレーション インタラクション法と結合クラスター法は精度が高くなりますが、計算コストは指数関数的に増加します。密度汎関数理論 (DFT) 法は計算コストが比較的低いものの、精度には限界があります。深層学習の強力な非線形フィッティング能力により、DeepMind は波動関数の近似解を達成するために FermiNet を提案しました。
分子内の電子は、原子核や他の電子と相互作用するだけでなく、パウリの排他原理に従う必要があります。つまり、2 つのフェルミオンは同じ量子状態になることはできず、フェルミオン交換後の波動関数は非対称性を持ちます。つまり、2 つのフェルミオンが交換されるときです。状態では、波動関数は反対の符号を持たなければなりません。波動関数の反対称性に関しては、行列式は当然一貫しているため、波動関数を表すためにスレーター行列式を使用することが量子化学では広く使用されています。
**1. **ネットワークアーキテクチャ
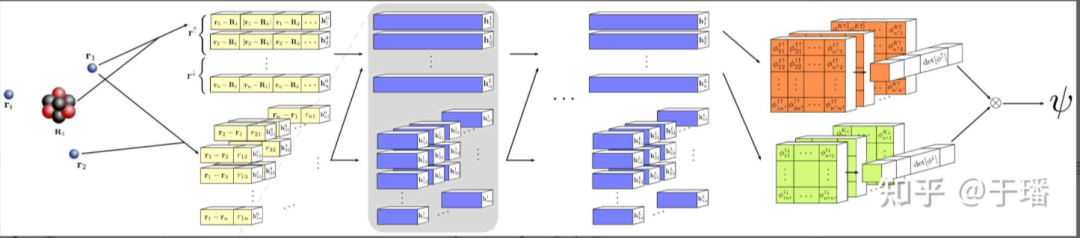図1 FermiNetネットワークの全体構成
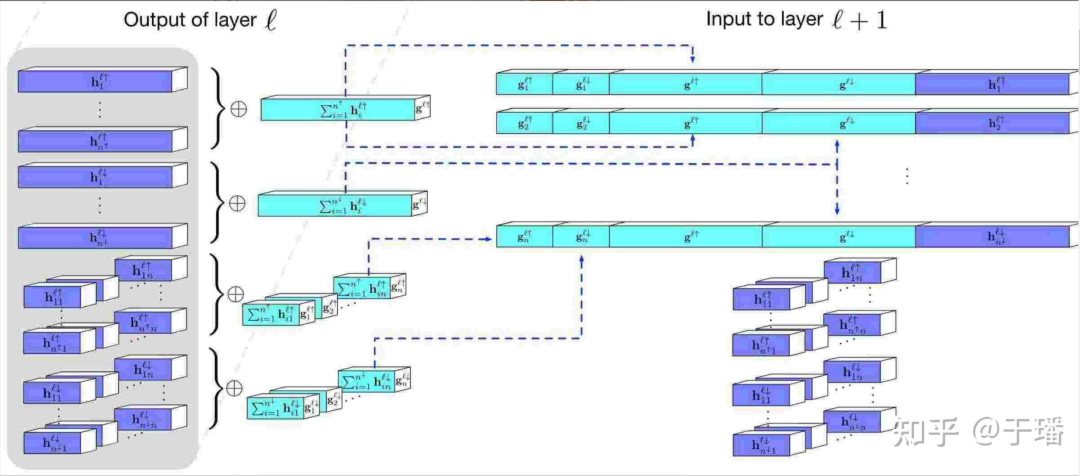図 2 ネットワーク層間の情報フロー転送
FermiNet のネットワーク全体のアーキテクチャを図 1 に、ネットワーク層の部分拡大図を図 2 に示します。ネットワーク内の各電子は個別の情報の流れを持つだけでなく、ネットワーク層で情報が伝達される際に、各電子は他の電子の情報や電子間の相互作用を統合し、元の単一電子軌道を置換を満たす軌道に置き換えます。多電子波動関数 (式 1) は最終的な波動関数 (式 2) を構成し、従来のスレーター行列式よりも強力な表現能力を持ちます。
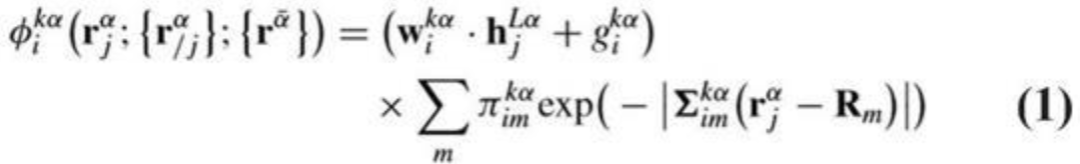
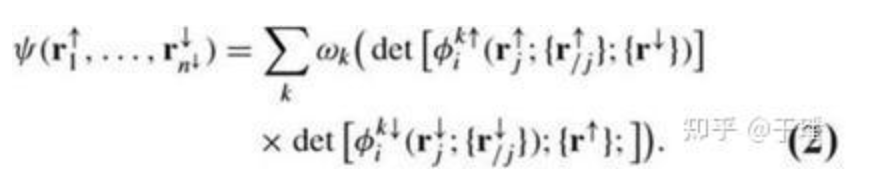
ネットワークがトレーニングを開始する前に、トレーニング プロセスの安定性を向上させ、トレーニング時間を短縮するために事前トレーニングが実行されます。事前学習された損失は、参照として設定された STO-3G 基底の Hartree-Fock 方程式の解を使用し、損失関数は式 3 に示されます。
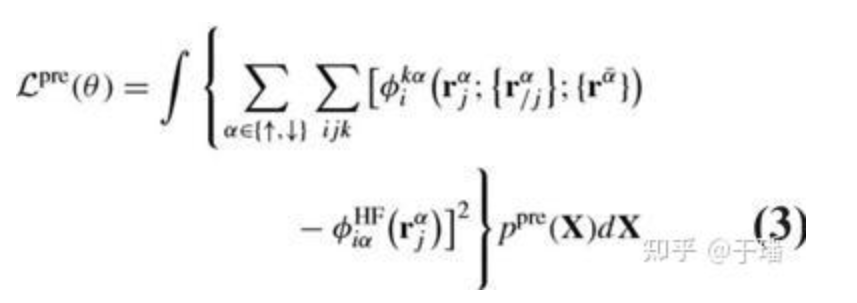
ネットワーク トレーニングの場合、式 4 に示すように、損失関数としてエネルギー期待値を使用した変分モンテカルロに基づいています。具体的には、エネルギーは式 5 で表すことができ、エネルギー勾配は式 6 のように計算されます。また、ネットワークパラメータを効率的に最適化するために、自然勾配法を近似したKFAC二次オプティマイザを採用しています。
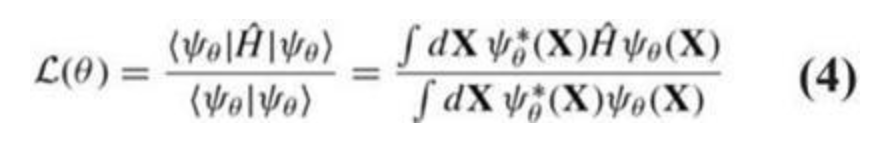
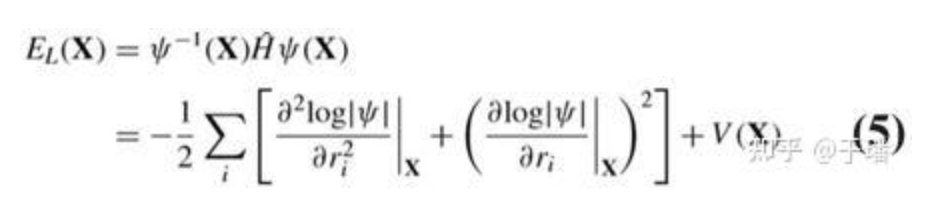
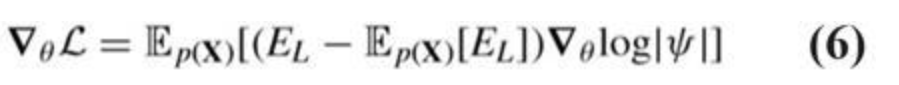
**2、**実験結果
FermiNet の精度は従来の VMC 法を上回り (表 1 に示すように)、限られた基底系の下では CCSD(T) 法よりも優れています。これは、FermiNet が基底系を使用せず、基底系の外挿の問題がないためです。 。
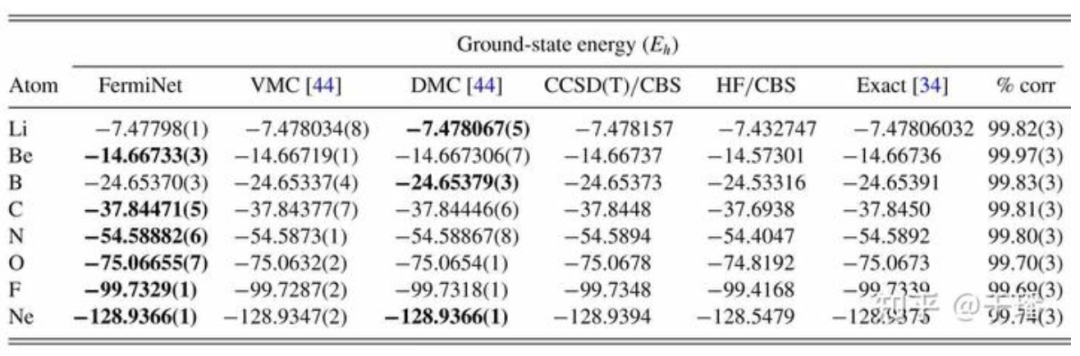表1 基底状態エネルギー値（太字部分はFermiNet、VMC、DMCにおける正確な値に最も近い項目）
CCSD(T) は平衡幾何学に対して非常に正確ですが、低励起状態にある分子、伸長、ねじれ、または平衡幾何学から外れた分子に対しては制限があり、FermiNet ほど良好ではありません。結果を図 3 に示します。 。
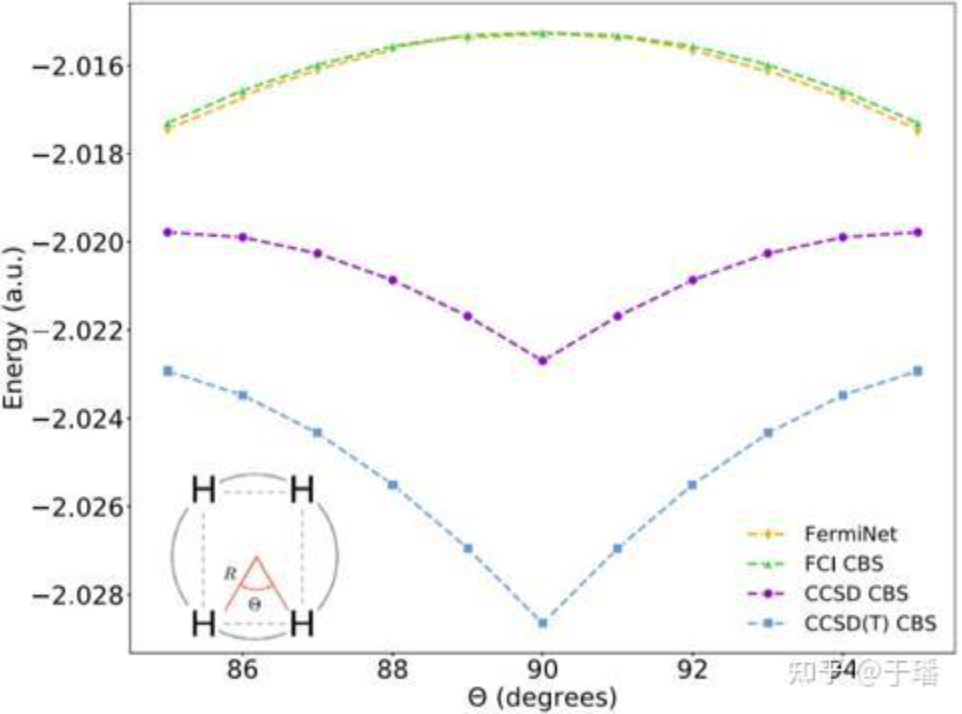図3 分子H4のエネルギー曲線
図 4 に示すように、窒素分子の窒素-窒素三重結合解離については、FermiNet は無制限の CCSD(T) メソッドよりも優れています。
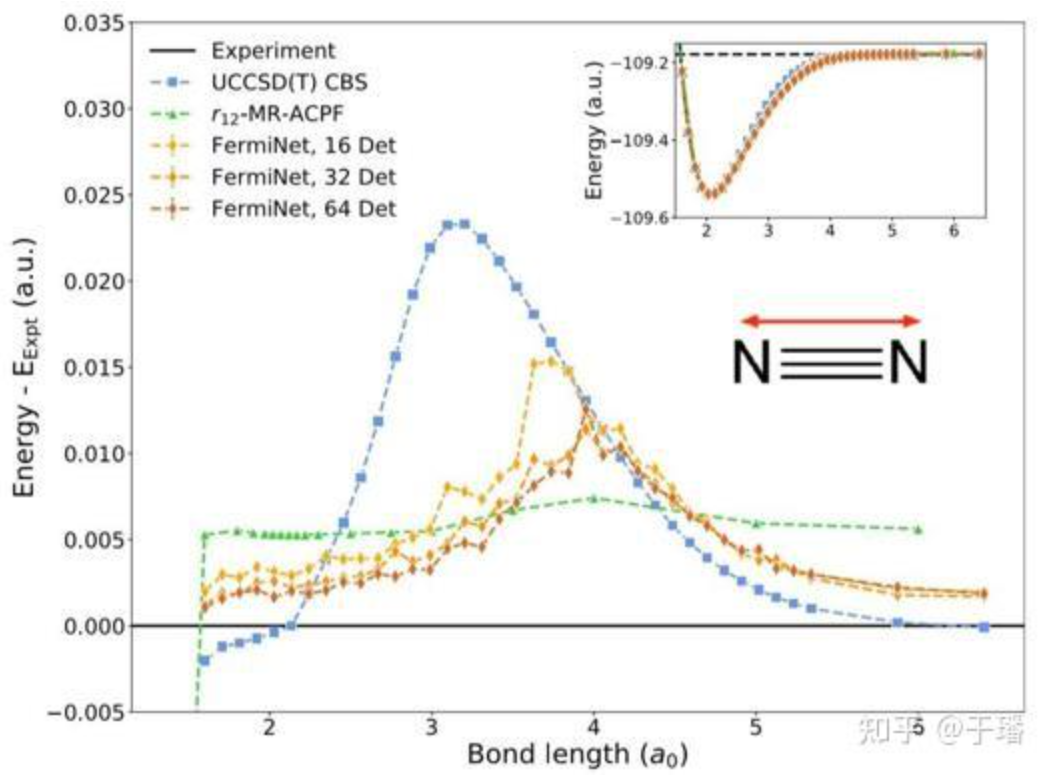図4 窒素-窒素三重結合解離のエネルギー曲線
**3、**概要
FermiNet はネットワーク層で単一電子と複数電子間の情報を融合し、単一電子の軌道を置換等分散を満たす複数電子の波動関数に置き換えることで、従来の VMC 法を上回る精度を実現するだけでなく、より高精度な波動関数解を実現します。 CCSD(T) 法は、非平衡幾何構造や窒素-窒素三重結合解離などの難しいシステム構造に適しています。 FermiNet の成果は、研究者が量子化学の分野で新しいまたはより優れたネットワーク アーキテクチャを提案することを奨励し、それによってより効率的で正確な波動関数ソリューションを実現します。
参考文献
[1] Pfau D、Spencer JS、Matthews AGDG、他。ディープ ニューラル ネットワークを使用した多電子シュレディンガー方程式の非経験的解法[J]。フィジカルレビューリサーチ、2020、2(3): 033429。
DOI: https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033429
1990 年代生まれのプログラマーがビデオ移植ソフトウェアを開発し、1 年足らずで 700 万以上の利益を上げました。結末は非常に罰的でした。 Google は、Flutter、Dart、Python チームの中国人プログラマーの「35 歳の呪い」に関係する人員削減を認めた 。Microsoft は 、 無力な中年者にとっては幸運なおもちゃでもある。強力で GPT-4.5 の疑いがある; Tongyi Qianwen オープンソース 8 モデルWindows 1.0 が 3 か月以内に正式に GA Windows 10 の市場シェアは 70% に達し、Windows 11 GitHub がAI ネイティブ開発ツール GitHub Copilot Workspace JAVAをリリースOLTP+OLAP を処理できる唯一の強力なクエリです。これが最高の ORM です。