共有者: Wu Shaojun ｜学校**: 中国電子科学技術大学**
簡単な紹介
量子多体システムをシミュレーションする際の複雑さの指数関数的増加を克服することは、物理学における困難な目標です。現在、一次元量子システムの基底状態特性については、テンソル ネットワーク状態 (TNS) に基づく方法が、基本的に正確な数値解を与える効果的な方法を提供しています。 2 次元システムでは、さまざまな格子モデルに対して TNS を最適化するいくつかのアルゴリズムを導入することによって、ある程度の進歩も見られました。今回は、2 次元系の量子状態を記述するのに使用でき、計算上の利点がある新しい量子状態表現法であるアイソメトリック TNS を紹介します。また、局所測定を使用してそれを実現する方法も紹介します。量子状態を再構築する MPS を構築する方法。線形数の演算のみを使用します。
関連論文1
**タイトル:二次元における等尺性テンソル ネットワーク状態
著者: Michael P. Zaletel および Frank Pollmann
ジャーナル: **Phys. Rev. Lett. 124、037201 (2020)
**公開日:** 2020 年 1 月 24 日
関連論文2
**クレジット:効率的な量子状態トモグラフィー
クレジット: Marcus Cramer、Martin B. Plenio、Steven T. Flammia、Rolando Somma、David Gross、Stephen D. Bartlett、Olivier Landon-Cardinal、David Poulin、Yi-Kai Liu
:** Natureコミュニケーションズ 1, 149(2010)
**公開日:** 2010 年 12 月 21 日
01
**導入
**
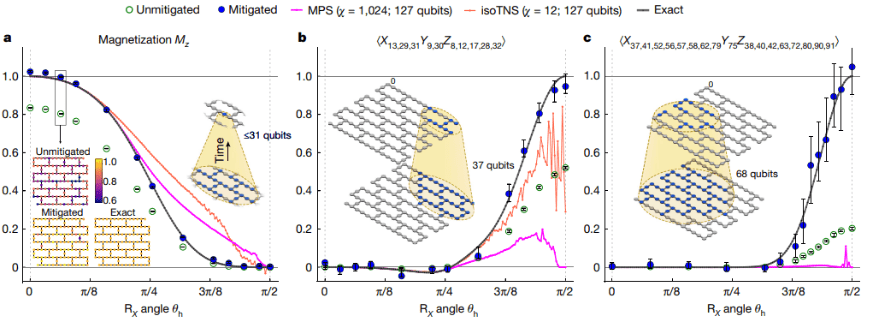
(画像出典: Nature volume 618、pages500–505 (2023))
最近、IBM は 127 個の量子プロセッサ上で 2 次元横磁場イジング モデルのシミュレーションを実装しました。正確な結果を得るには、古典的なシミュレーションを使用する必要があります。この研究では、ウェイト 1、ウェイト 10、ウェイト 17 の観測を使用して 5 ステップ トロッターの量子回路を測定し、実験結果を図に示します。
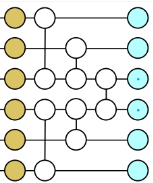
正確な解を得るために古典的なシミュレーションを実行する場合、ここでは Light-cone and Depth-Reduced (LCDR) 法が使用されます。これは 2 つの部分に分かれており、1 つは量子ゲート間の特性を通じてシミュレーションする必要がある回路層の数を減らすことであり、もう 1 つは観測量 A に関連する量子ビットが局所的であると考えることです。 Evolution では、127 ビットすべてではなく、量子ビットの一部のみを考慮する必要があります。重み 1、重み 10、重み 17 の観測に関連する量子ビット数は、それぞれ 31、37、68 です。 68 量子ビットでのシミュレーションは依然として古典的なコンピューターによる総当りシミュレーションの能力を超えていることは注目に値します。したがって、この研究では、シミュレーション用にテンソル ネットワーク、1D 行列積状態 (MPS) および 2D アイソメトリック テンソル ネットワーク状態 (iso TNS) を導入します。
02
**マトリックス積状態 (MPS) の概要
**
1. テンソルの基礎知識
(1) 定義と図表
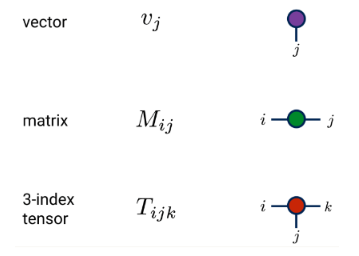
(2) 同一指標の縮小
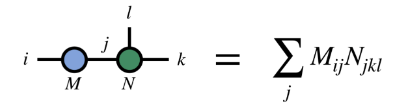
2、MPS
N 個の格子点を持つ 1 次元系の場合、各格子点が d 個の量子状態を持つ場合、多体ヒルベルト空間は格子ヒルベルト空間のテンソル積として表すことができます。
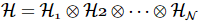
対応する任意の複数の姿勢は次のように表現できます。
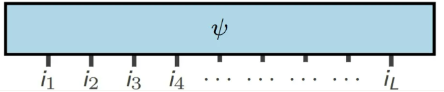
(画像ソース: arXir:1603.03039、2016)
行列積状態 (MPS) の中心的な考え方は、多体状態を次のように表現することです。
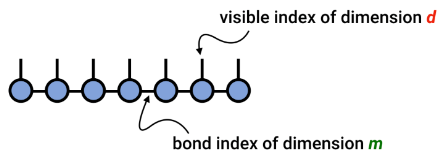
(画像ソース: arXir:1603.03039、2016)
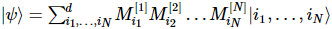
各ユニットは 3 次テンソルであり、物理インデックスは格子点の量子状態であり、補助インデックスはそれと左右のシステム間の量子もつれとみなすことができます。
SVD 分解:
一般的な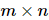
複素行列 A の場合、次のような分解が行われます
。
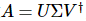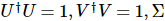は
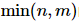次元 の対角行列であり、対角上の要素は特異値と呼ばれます。一般的に、特異値は対角線に沿って最大から最小の順に配置されます。
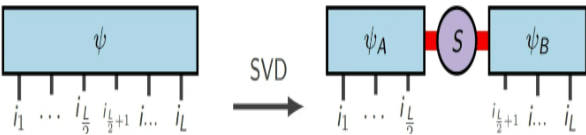
(画像ソース: arXir:1603.03039、2016)
ここで、S は特異値を表します。システムの 2 つの部分間のもつれが強くない場合、特異値のスペクトルは急速に減衰する傾向があり、行列の情報の大部分を保持するために保持する必要がある特異値の数は少なくなります。シュミット分解の各グループが m 個以下の特異値を保持すると規定すると、最終的には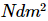
この多体状態を近似的に表すために実数のみが必要になります。 1 つのパラメーターを必要とする元の表現方法と比較して
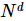、この表現は格子点の数に対して線形空間の複雑度を持ち、効率は元のテンソル積表現の指数関数的増加の複雑度よりもはるかに高くなります。
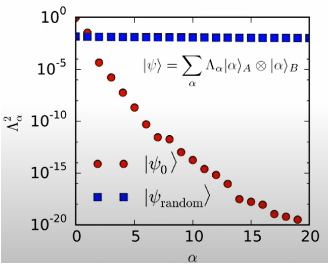
(画像ソース: arXir:1603.03039、2016)
MPS を取得するプロセス:
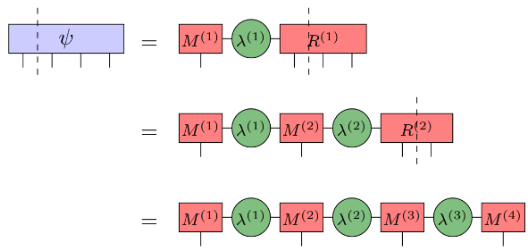
(画像ソース: arXir:1603.03039、2016)
なぜなら：
状態のような多体演算子の場合、行列積形式 (MPO) で多体演算子を書くことができます。
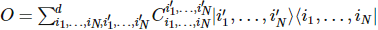
状態とは異なり、ローカル演算子で構成されるハミルトニアンは、当然のことながら行列積の形式で記述することができます。
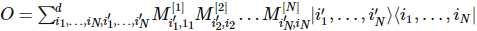
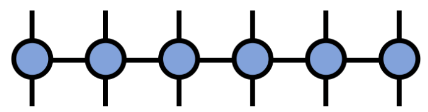
(画像ソース: arXir:1603.03039、2016)
行列積演算子は、行列積の状態に作用した後も行列積の構造を維持します。
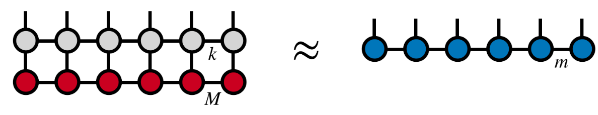
(画像ソース: arXir:1603.03039、2016)
03
2 次元のアイソメトリック テンソル ネットワーク状態
1. 概要
テンソル ネットワーク状態は、2 次元量子多体問題に対する有望ではありますが、数値的に困難なツールです。この記事では、著者らは、テンソル ネットワークの効率的な縮小を可能にする形式である等尺性制限 TNS ansatz を紹介します。 Ansatz を数値的にベンチマークするために、著者らはまず、2 次元横磁場イジング モデルの基底状態の MPS 表現を isoTNS に効果的に変換できることを実証しました。実際、著者らは 2D TEBD アルゴリズムを実装し、それが効果的に機能することを示しました。 2D モデルの基底状態の近似値を求めます。
2.等尺性テンソルネットワーク状態
1) アイソメトリ条件: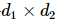
次元行列 M の場合、または
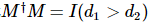。テンソル図では、一般に矢印は直交性を示すために使用されます。これは、テンソルとその共役テンソルの内向きインデックスを縮小することによって単位行列が取得されることを規定します。
2) MPS の正規形式:
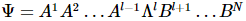
このうち、AとBは左右の直交条件を満たします。左の直交条件は、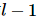
前の量子の短縮とそれ自体の転置が単位行列であることを意味し、右の直交条件は、
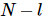次の量子の短縮とそれ自体の転置が単位行列であることを意味し、
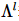対角要素が減少することを表します。対角行列は直交中心とも呼ばれます。
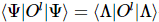3)外部 AB テンソルはアイソメトリ条件に従って 1 に縮小するため、ローカル操作の期待値は次のように直接取得できます。
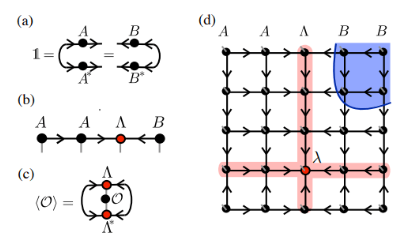
(画像出典: Phys. Rev. Lett. 124、037201)
- 2 次元に一般化します。
上記の式から類推すると、TNS の各行と列がアイソメトリであることが要求されます。この制約は、各テンソルがアイソメトリであることを要求することによってさらに要求される可能性があります。上の図 d に示すように、赤い部分は内向きの矢印しかありません。したがって、これは TNS の 1 次元の「直交超曲面」であり、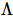
標準直交基底に基づく波動関数であるため、
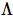MPS と同様に処理できます。それ自体を 1 次元の正準形式に置くことができます (その直交中心は 1 次元の正準アルゴリズムを使用して自由に移動できます)。どの演算子にもがあり、
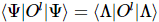つまり、さらなる近似を行わずに標準 MPS アルゴリズムによって効率的に計算できる 1 次元の期待値の次元削減が存在します。これは、期待値を得るためにネットワーク全体のおおよその縮小を使用する必要がある一般的な TNS とは大きく対照的です。
3. 直交超曲面の移動
中心直交形式は、直交超曲面 Lammda がネットワーク全体で効率的に移動できる場合にのみ計算上役立ちます。 1 次元では、任意の直交行列の分解 (QR または SVD) を通じて直交中心の移動を実現できます。 2 次元では、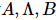
列全体を移動する必要もあります。しかし、2 次元システムの場合、直交行列分解の方法は、
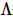MPS として表現するために必要な局所性を破壊するため無効です。
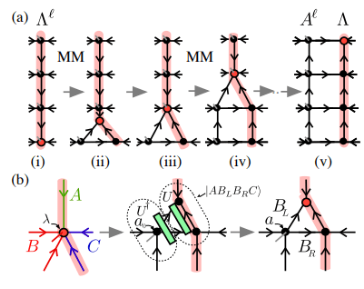
(画像出典: Phys. Rev. Lett. 124、037201)
この記事では、著者は Moses Move メソッドを使用して直交面の中心を移動します。上の図に示すように、MM アルゴリズムの後、直交超曲面は、物理インジケータなしの左直交状態とゼロ列状態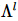
の積に分割されます。このうち伸長は、図(b)に示す「分割」処理を連続的に適用することで実現します。中心点のインデックスは3 つの状態にグループ化され、2 つのステップで 3 つのテンソルに「分割」されます。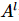
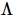
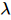
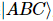
4. MPS を isoNTS に拡張
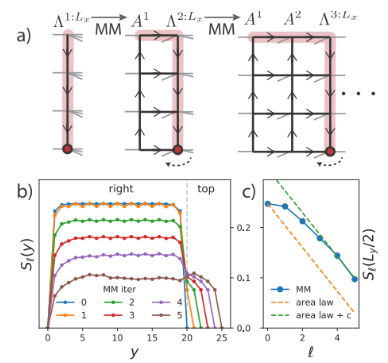
(画像出典: Phys. Rev. Lett. 124、037201)
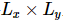著者らは、基底状態の波動関数を与えて、 isoTNS に組み込む
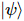ことができる反復アルゴリズムを提案し、シング横磁場モデルをテストしました。ストリップを考慮し、DMRG を使用して1D MPS の基底状態を取得します。ここで、各「サイト」には対応するスピンの行が含まれます [図 (a)]。図 a の 3 番目のパネルに示すように、MM を使用して波動関数の列を繰り返し「分割」し、isoTNS を生成できます。この例では、結合次元は 6 として選択されます。g=3.5 (常磁性相) の場合、各サイトの誤差は です。この場合、。結果は図 b に示されており、直交超曲面に沿ったセグメンテーションのエンタングルメント エントロピーは、反復回数が増加するにつれて減少することがわかります。図 c は、反復回数が増加するにつれて、もつれのエントロピーが直線的に減衰することを示しており、これは予想どおりです。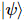
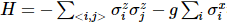
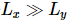
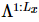
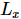
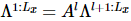
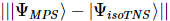
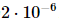
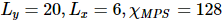
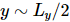
5.
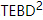アルゴリズム
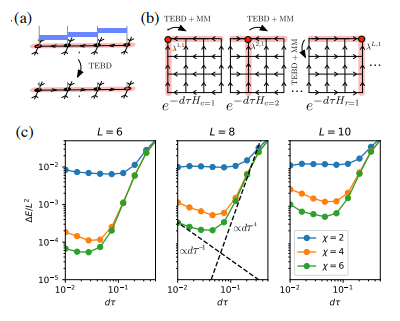
(画像出典: Phys. Rev. Lett. 124、037201)
また、著者は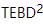
アルゴリズムを実装しました。TEBD の主なアイデアは、トロッター-スズキ分解に基づくアニーリング アルゴリズムを使用して、ランダムに初期化された MPS 状態を基底状態に進化させ、その進化プロセスをテンソル ネットワーク収縮問題に変換することです。 TEBD アルゴリズムを使用して収縮を解決します。具体的には、isoTNS に対して Trotterized タイムステッパーが提案されており、仮想時間発展を通じて基底状態を取得できます。最近隣相互作用のみがあると仮定して、図 (a) に示すように、ハミルトニアンを列と行に作用する項に分割し
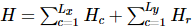、Trotterized を実行します。 
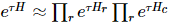1D TEBD アップデートの場合、
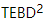2 次まで簡単に改善できます。直交中心から開始
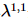し、標準の 1D TEBD アルゴリズムと MM アルゴリズムを呼び出して、徐々に直交中心を移動します。 1 回のスキャンでは、アルゴリズムは実際には 1D TEBD の 2 つのネストされたバージョンであるため、 という名前が付けられています
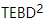。このうち、
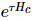の進化は 1D TEBD を呼び出すことで実現され、その複雑度は
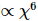MM ですが、制約なし PEPS の完全な更新複雑度は です
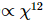。図 (c) は、g=3.5 横磁場イジング モデルのエネルギー誤差密度を、さまざまなシステム サイズと最大結合寸法に対する
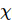トロッター ステップ サイズの関数として示しています
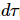。結合サイズ
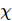が増加するにつれて、最小エネルギーは正確な結果に向かって収束します。
04
効率的な量子状態トモグラフィー
1. 概要
測定データから量子状態を推測することは、システムのサイズに応じて指数関数的に増加する測定値の数とそれらの処理に必要な計算量が増加するため、大規模なシステムでは実行不可能になります。この記事では、システムサイズの直接断層撮影よりも有利な断層撮影スキームを提案します。この方法は、一定数のサブシステムの均一な操作を必要とし、線形数の実験操作のみに依存します。このスキームは、広範囲の量子状態、特に MPS に適用できます。
2. ユニタリ変換に基づくスキーム
このメソッドの中心的な考え方は、チェーンを左から右に解くための一連の操作を見つけることです。このシーケンス内の各操作はローカルであり、次元 N とは独立しています。
理想状態が であると仮定し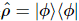
、この量子状態が与えられた結合次元 R を持つ MPS であると仮定します。この方法の目的は、これを再構築することです
。
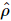アルゴリズムプロセス:
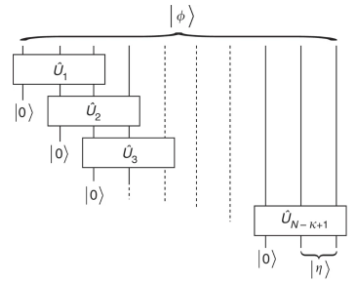
(画像出典: Nature Communications 1, 149 (2010))
1) まず、 を取得し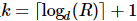
、最初の k サイトで標準量子状態トモグラフィーを実行します。その後、最初の k サイトの換算密度行列は次のようになります。この
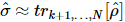換算密度行列には固有分解があります
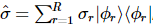。したがって、ランク R と固有値和が同じ
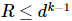量子ビットが 1 つ少ない密度行列が存在します。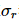
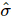
2) 次に、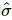
その情報をさらに使用して、最初の k 位置のユニタリ行列を構築します
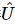。これにより、
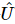最初のサイトのもつれが解消されます。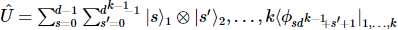
3).
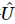アクションを元の状態に適用して取得します。
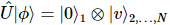その中には、位置にある純粋な状態
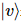がいくつかあります
。
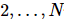4) 次に、次の 2 番目から k+1 番目の位置について上記のプロセスを繰り返します。類推により、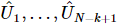
それぞれが位置
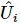で機能する一連のユニタリ行列を取得できます
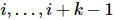。このシーケンスは となり
、
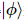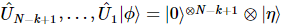それぞれが位置
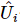で動作します
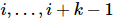。このシーケンスにより、 が作成されます
。
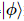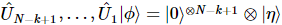ここで、 は、
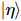最後の k-1 位置での純粋な状態です。
要約すると、このスキームは MPS を準備するための量子回路を推定します。MPS 分解は、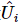
とによって簡単に取得できます。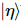
3. 誤差
この手法の誤差は主に 2 つの側面から生じます。1 つは結合次元の制限により量子状態を完全に表現できないこと、もう 1 つは測定に起因する誤差です。
推定された解きほぐされたユニタリ行列 が与えられると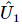
、任意の状態は
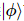次のように表現できます。
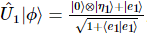ここで、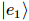
は誤差ベクトルです。
次のステップでは、次の形式で状態を取得できます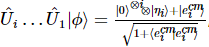
。
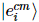は累積誤差です。
標準基底で最初の i 個の粒子を測定し、すべてのゼロの結果を事後選択することで、この誤差ベクトルを切り捨てることができます。これが起こる確率はおよそ で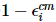
、システムはそのままの状態になります
。
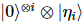一連のユニタリ変換後の最終状態は次のようになります。
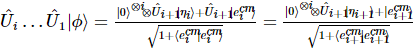
その中で、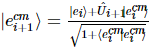
したがって、
。
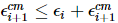粒子の数に応じて誤差が直線的に累積し、取得した MPS が次のように記録されることがわかります。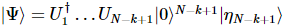
すると、次のようになります。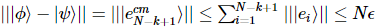
で、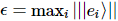
。全体的な誤差は、最大でも各ステップの個別の誤差の合計です。
1990 年代生まれのプログラマーがビデオ移植ソフトウェアを開発し、1 年足らずで 700 万以上の利益を上げました。結末は非常に罰的でした。 Google は、Flutter、Dart、Python チームの中国人プログラマーの「35 歳の呪い」に関係する人員削減を認めた 。Microsoft は 、 無力な中年者にとっては幸運なおもちゃでもある。強力で GPT-4.5 の疑いがある; Tongyi Qianwen オープンソース 8 モデルWindows 1.0 が 3 か月以内に正式に GA Windows 10 の市場シェアは 70% に達し、Windows 11 GitHub がAI ネイティブ開発ツール GitHub Copilot Workspace JAVAをリリースOLTP+OLAP を処理できる唯一の強力なクエリです。これが最高の ORM です。