2022 Huashu Cup 종이 아이디어 분석 + 완성 코드(수중 로봇 조립 계획)

공식 분석 영상을 보시면 됩니다.(이 영상이 참가자라면 무료로 시청하실 수 있습니다. 못보신 분들을 위해 며칠 내로 블로그 제작을 고려해볼 예정입니다.) 또한 , 이 블로그 말미에 공식 표준 답변을 넣었습니다. , 참고용으로.
2022화슈컵 문제 B 공식 분석 영상》》》》》》》

다음은 성명서입니다. 나는 C 질문으로 Huashu Cup에 참가하고 있습니다. 논문과 코드에는 다른 사람들이 참조하지만 실제로이 블로그에서 내가 그렇게 열심히 분류했습니다. 저도 초보자이고 저도 그냥 정리해서 보냈습니다. 아이디어는 스스로 학습하기에 편리하고 참고용일 뿐입니다. 우수한 논문이나 표준 답변은 없습니다.

전체 제목:
링크: https://pan.baidu.com/s/16E1X35O13NWIij72OClVgQ?pwd=1234
추출 코드: 1234

1. 주제

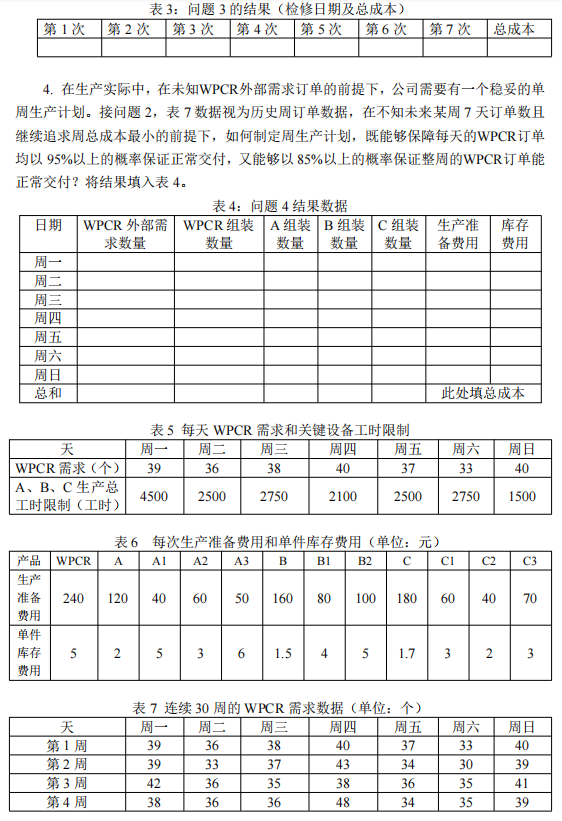
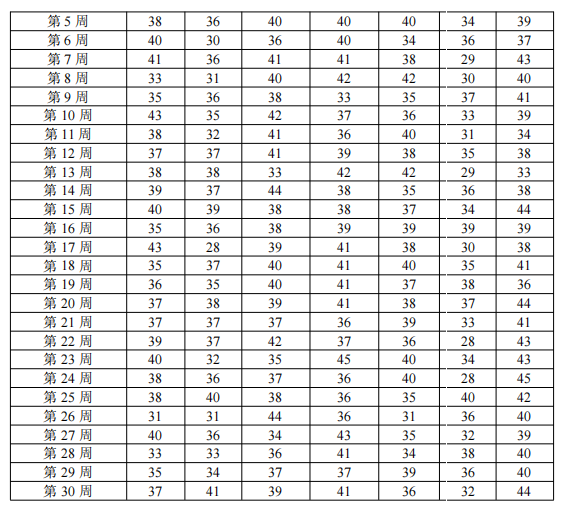
2. 문제 분석

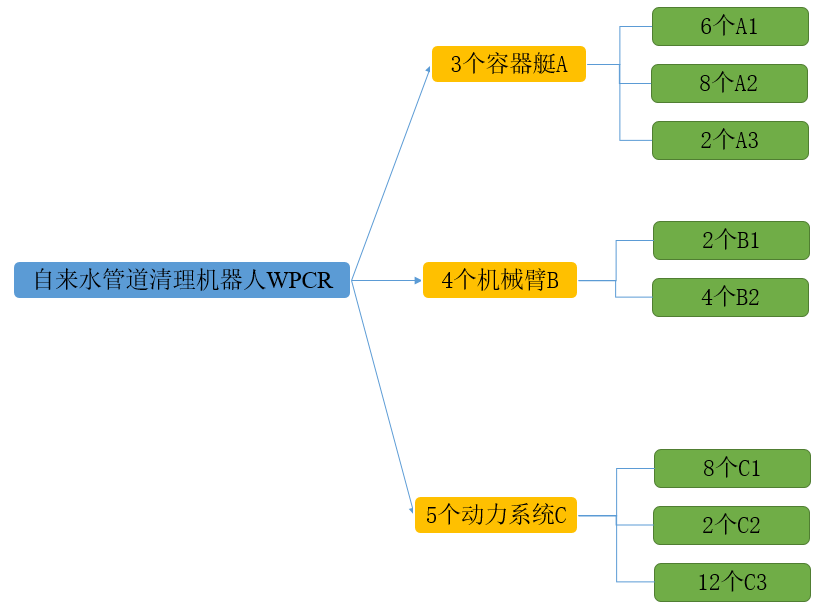
3. 모델 가정

1. 작은 부품을 조립하기 위한 충분한 재료.
2. 생산과정에서 공장정전, 기계고장 등 예기치 못한 상황으로 인해 생산이 중단되지 않습니다.
3. 공장의 자본 흐름은 정상이며 자본 부족으로 인해 생산에 영향을 받지 않습니다.
4. 최종 제품 로봇만 외부 수요가 있으며 다른 구성 요소는 외부에서 판매되지 않습니다.
5. 로봇 수요는 계획에 따라 결정되며 시장 가격 변동에 영향을 받지 않습니다.

4. 기호 설명

상징	설명하다	단위
디	날	하늘
MA1 d , MA2 d , MA3 d … MC3 d	d일의 위젯 조립 수량	개인
SA1 d , SA2 d , SA3 d … SC3 d	d일의 위젯 잔여 수량	개인
MA d , MB d ,MC d	d일의 대형 부품 조립 수량	개인
SA d , SB d , SC d	d일의 대형 부품 잔여 수량	개인
DW d	d일에 요구되는 로봇의 수	개인
MW 디	d일에 조립된 로봇의 수	개인
SW 디	d일의 남은 로봇 수	개인
티 _	d일의 총 근무 시간 제한	근무 시간
RA1,RA2,…RB,RC	구성 요소의 단위당 저장 비용	원
FA1,FA2,…,FB,FC	부품의 생산 준비 비용	원
XW d	d일에 로봇을 생산할지 여부에 대한 0-1 변수	-
R d	d일의 재고 비용	원
에프디 _	d일의 생산 준비 비용	원
체크날짜 t	t차 점검일자	하늘
티빅 디	d일의 총 근무 시간 제한	근무 시간
DW예측 d	미래의 d번째 요일에 요구되는 로봇의 수	개인

5. 문제 1 모델의 수립 및 해결

5.1 문제 모델의 수립

5.1.1 작은 구성 요소는 큰 구성 요소를 조립

여기서는 대형 부품 A의 조립을 예로 들어 설명합니다. 큰 부품 A를 조립하려면 6개의 작은 부품 A1, 8개의 작은 부품 A2, 2개의 작은 부품 A3이 필요합니다.

d일에 큰 부품 A를 조립하는 데 사용된 작은 부품 A1의 수는 d일(현재 날짜)에 조립된 작은 부품의 수 MA1 _d 와 d-1일(어제)에 남아 있는 작은 부품 의 수 입니다 . SA1 _d-1 , 즉 MA1 _d +SA1 _d-1 . 위젯 A2, A3의 개수도 같은 방법으로 구할 수 있습니다.

큰 부품 A를 조립하려면 6개의 작은 부품 A1이 필요합니다. A1만 고려하면 조립할 수 있는 최대 부품 수는 다음과 같습니다.

$$\left[\begin{array}{c}\frac{MA1\_{}_{}+사1\_{}_{d-}}{6}\end{array}\right]\text{\hspace{1em}( 1 )}$$

참고: 여기서 [ ] 기호는 반올림됩니다. 즉, 자신보다 작은 가장 큰 정수를 취합니다.

마찬가지로 A2만 고려하는 경우 조립할 수 있는 대형 부품 A의 최대 수는 다음과 같습니다.

$$\left[\begin{array}{c}\frac{MA2\_{}_{}+사2\_{}_{d-}}{8}\end{array}\right]\text{\hspace{1em}( 2 )}$$
A3만 고려하는 경우 조립할 수 있는 대형 부품 A의 최대 수는 다음과 같습니다.

$$\left[\begin{array}{c}\frac{MA3\_{}_{}+사3\_{}_{d-}}{2}\end{array}\right]\text{\hspace{1em}( 3 )}$$

따라서 d일에 대형 구성품 A의 최대 조립품 수는 다음과 같습니다.

$$분\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+사1\_{}_{d-}}{6},\frac{MA2\_{}_{}+사2\_{}_{d-}}{8},\frac{MA3\_{}_{}+사3\_{}_{d-}}{2}\end{array}\right)\right]\text{\hspace{1em}( 4 )}$$

참고: 반올림해야 합니다.

하루에 필요한 로봇의 수는 다르며, 주문의 수요를 충족시키기 위해 공장에서 대형 부품 A를 조립할 때 반드시 최대값과 같을 필요는 없습니다. 따라서 d일에 대형 구성품 A의 조립품 수량이 다음 제약 조건을 충족해야 합니다.

$$MA{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+사1\_{}_{d-}}{6},\frac{MA2\_{}_{}+사2\_{}_{d-}}{8},\frac{MA3\_{}_{}+사3\_{}_{d-}}{2}\end{array}\right)\right]\text{\hspace{1em}( 5 )}$$

같은 방식으로 d일에 대형 구성품 B와 C의 조립 수량은 다음 제약 조건을 충족해야 합니다.

$$엠비{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{메가바이트1_{}+SB{1}_{d-}}{2},\frac{메가바이트2_{}+SB{2}_{d-}}{4}\end{array}\right)\right]\text{\hspace{1em}( 6 )}$$

$$엠씨{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MC{1}_{}+SC{1}_{d-}}{8},\frac{MC{2}_{}+SC{2}_{d-}}{2},\frac{MC{2}_{}+SC{2}_{d-}}{12}\end{array}\right)\right]\text{\hspace{1em}( 6 )}$$

5.1.2 남은 위젯

큰 부품과 작은 부품을 조립한 후 작은 부품이 남을 수 있습니다. 여기서는 위젯 A1을 예로 사용합니다.
d일에 위젯 A1의 나머지 수는 d일 MA1 _d 에 조립된 위젯 수의 합 과 d-1일 SA1 _d-1 에 남아 있는 위젯 수 의 합에서 수의 합을 뺀 값 을 충족해야 합니다. d d-1일의 위젯 수 Al의 소비. 큰 부품 A를 조립하려면 6개의 작은 부품 A1이 필요합니다. 따라서 d일의 Al 소모량은 6×MA _d 이다. 따라서 _d일 에 A1의 잔여 수량 SA1d 는 다음과 같습니다.

$$사1\_{}_{}=MA1\_{}_{}+사1\_{}_{d-}-6*MA{\_}_{}\text{\hspace{1em}( 7 )}$$

오늘의 - 소비된 = 남은 것
(오늘의 조립 + 어제의 남은 것) - 소비된 = 남은 것

다른 작은 구성 요소의 나머지 수는 같은 방식으로 얻을 수 있습니다.
$$사2\_{}_{}=MA2\_{}_{}+사2\_{}_{d-}-8*MA{\_}_{}$$
$$사3\_{}_{}=MA3\_{}_{}+사3\_{}_{d-}-2*MA{\_}_{}$$
$$SB{1}_{}=메가바이트1_{}+SB{1}_{d-}-2*엠비{\_}_{}$$
$$SB{2}_{}=MA1\_{}_{}+사1\_{}_{d-}-4*엠비{\_}_{}\text{\hspace{1em}( 8 )}$$
$$SC{1}_{}=MC{1}_{}+SC{1}_{d-}-8*엠씨{\_}_{}$$
$$SC{2}_{}=MC{2}_{}+SC{2}_{d-}-2*엠씨{\_}_{}$$
$$SC{3}_{}=MC{3}_{}+SC{3}_{d-}-12*엠씨{\_}_{}$$

5.1.3 로봇의 조립 수량에 따른 나머지 대형 부품의 계산

로봇의 조립, 즉 큰 부품으로 로봇을 조립하는 것은 큰 부품을 작은 부품으로 조립하는 것과 동일하므로 d일에 조립되는 로봇의 수는 다음과 같습니다.

$$남{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+사1\_{}_{d-}}{삼},\frac{메가바이트2_{}+SB{2}_{d-}}{4},\frac{MC{2}_{}+SC{2}_{d-}}{5}\end{array}\right)\right]\text{\hspace{1em}( 9 )}$$

이 중 MW _d 는 로봇 조립 대수, MA _d 는 d일의 대형 부품 A 조립 수, SA _d-1 은 d-1일의 나머지 대형 부품 A의 조립 수이다.

약간의 잔여물이 있을 수 있는 대형 부품으로 로봇을 조립합니다. 남은 위젯 수를 계산하는 것과 같은 방식으로 다음과 같이 계산합니다.

$$사{\_}_{}=MA{\_}_{}+사{\_}_{d-}-삼*남{\_}_{}$$
$$에스비{\_}_{}=엠비{\_}_{}+에스비{\_}_{d-}-4*남{\_}_{}\text{\hspace{1em}( 10 )}$$
$$에스{씨}_{}=엠씨{\_}_{}+에스{씨}_{d-}-5*남{\_}_{}$$

5.1.4 로봇 조립 수량 제약

공장에서 접수된 모든 로봇 주문은 만기 시 배송되어야 하므로 d일 로봇 조립 수량 MW _d 와 d-1일 로봇 잔여 수량 SW _d 의 합이 수요 수량보다 커야 합니다. DW d 일 _d .
$$남{\_}_{}+SW{\_}_{d-}⩾DW{\_}_{}\text{\hspace{1em}( 12 )}$$

5.1.5 남은 로봇

일일 주문 봇 판매 후 잔여물이 있을 수 있습니다. d일 로봇 의 잔여 SW _d 는 d일 조립 수량 MW _d 와 d-1일 잔여 수량 SW _d-1 의 합에서 당일 주문 수량 DW _d 를 뺀 값입니다 . 이다

$$SW{\_}_{}=남{\_}_{}+SW{\_}_{d-}-DW{\_}_{}\text{\hspace{1em}( 12 )}$$

5.1.6 재고 없음 잔고 없음

1일은 재고 부품 없이 시작됩니다. 예:
$$사1\_{}_{}=사2\_{}_{}=사3\_{}_{}=SB{1}_{}=SB{2}_{}=SC{1}_{}=SC{2}_{}=SC{3}_{}\text{\hspace{1em}( 13 )}$$
$$사{\_}_{}=에스비{\_}_{}=에스{씨}_{}=0\text{\hspace{1em}( 13 )}$$

7일이 지나면 구성품 재고가 남지 않습니다.

$$사1\_{}_{}=사2\_{}_{}=사3\_{}_{}=SB{1}_{}=SB{2}_{}=SC{1}_{}=SC{2}_{}=SC{3}_{}$$
$$사{\_}_{}=에스비{\_}_{}=에스{씨}_{}=0\text{\hspace{1em}( 14 )}$$
$$SW{\_}_{}=0$$

5.1.7 근로시간 제한

A 1개를 만드는 데 3시간, B 1개를 만드는 데 5시간, C 1개를 만드는 데 5시간이 걸린다. 한 번에 다음 제약 조건을 충족해야 합니다.

$$삼\times MA{\_}_{}+5\times 엠비{\_}_{}+5\times 엠씨{\_}_{}⩽{티}_{}\text{\hspace{1em}( 15 )}$$

5.1.8 재고 수수료

하루가 끝날 때 부품의 재고가 있을 때 공장은 부품의 잔여 수량에 비례하는 일정 재고 수수료를 지불해야 합니다. 따라서 d일 부품의 잔여 수량에 따라 소형 부품, 대형 부품 및 로봇의 재고 비용을 표현할 수 있습니다.

$$Rs쇼핑몰A\_{}_{}=RA1\_\times 사1\_{}_{}+RA2\_\_\times 사2\_{}_{}+3\_\_\times 사3\_{}_{}$$

$$Rs쇼핑몰B\_{}_{}=RB1\times SB{1}_{}+RB2\times SB{2}_{}$$

$$Rs쇼핑몰C\_{}_{}=RC1\times SC{1}_{}+RC2\times SC{2}_{}+RC3\times SC{3}_{}\text{\hspace{1em}( 16 )}$$

$$알비지\_{}_{}=라\_\times 사{\_}_{}+RB\times 에스비{\_}_{}+RC\times 에스{씨}_{}$$

이 중 RA1은 대형 구성품 A의 단일 부품 재고 비용이고 SA1 _d 는 d일에 대형 구성품 A의 잔여 수량입니다. 다른 기호는 동일합니다. RsmallA _d , RsmallB _d 및 RsmallC _d 는 d일의 소형 구성품 A, B, C의 재고 비용이고, Rsmall은 d일의 대형 구성품의 재고 비용이며, R _d 는 해당 품목의 총 재고 비용입니다. 디데이.
합계는 d일의 재고 비용입니다.

$${아르\; 자형}_{}=Rs쇼핑몰A\_{}_{}+Rs쇼핑몰B\_{}_{}+Rs쇼핑몰C\_{}_{}+알비지\_{}_{}+RW\_\times SW{\_}_{}\text{\hspace{1em}( 17 )}$$

5.1.9 생산 준비 비용

공장에서 부품 제품을 생산할 때 생산량과 무관한 고정비를 생산준비비라고 하는데, 여기에 고정비 계산을 용이하게 하기 위해 0-1 변수를 도입한다. 생산 로봇 의 0-1 변수 XW _d 를 예로 들어 보겠습니다. 로봇이 d일에 생산되면 XW _d 는 1이고, d일에 로봇이 생산되지 않으면 XW _d 는 0입니다. 다음과 같이

$$X{여}_{}=\{\begin{array}{ll}1& 남{\_}_{}>0\\ & 남{\_}_{}=\end{array}\text{\hspace{1em}( 18 )}$$

다른 성분의 0-1 변수도 같은 방법으로 구할 수 있습니다.

따라서 모든 부품의 0-1 변수에 따라 소형 부품, 대형 부품 및 로봇의 생산 준비 비용을 표현할 수 있습니다.

$$F에스몰A\_{}_{}=XA{1}_{}\times FA1\_+XA{2}_{}\times FA2\_+XA{3}_{}\times FA3\_$$

$$F에스몰B\_{}_{}=XB{1}_{}\times FB1+XB{2}_{}\times FB2$$

$$F에스몰C\_{}_{}=XC{1}_{}\times FC1+XC{2}_{}\times FC2+XC{3}_{}\times FC3\text{\hspace{1em}( 19 )}$$

$$에프비지{\_}_{}=FA\_\times 엑스{에이}_{}+FB\times 엑스{비}_{}+FC\times 엑스{씨}_{}$$

이 중 XA1 _d 는 d일에 Al 생산 여부를 나타내는 0-1 변수이고, FA1은 Al의 생산 준비 비용이다.
다른 기호는 동일합니다. FsmallA _d , FsmallB _d , FsmallC _d 는 d일의 소형 부품 A, B, C의 생산 준비 비용과 d일의 Fbig 대형 부품의 재고 비용입니다. F _d 는 d일의 생산 준비 비용입니다.

합계는 d일의 생산 준비 비용입니다.
$${에프}_{}=F에스몰A\_{}_{}+F에스몰B\_{}_{}+F에스몰C\_{}_{}+에프비지{\_}_{}+X{여}_{}\times 여\_\text{\hspace{1em}( 20 )}$$

5.1.10 목적 함수

총 비용이 가장 작아야 합니다. 즉, 재고 비용과 생산 준비 비용의 합이 가장 작아야 하며 목적 함수를 얻을 수 있습니다.

$$분C=\sum _{d=1}{아르\; 자형}_{}+\sum _{d=1}{에프}_{}\text{\hspace{1em}( 21 )}$$

5.2 모델 문제 해결

시뮬레이션된 어닐링 알고리즘은 파티클 스웜 알고리즘과 결합되고 코드는 아래와 같이 문제 1의 결과를 얻기 위해 MATLAB으로 작성됩니다.

결과는 약간 문제가 있습니다. 7000+여야 합니다.

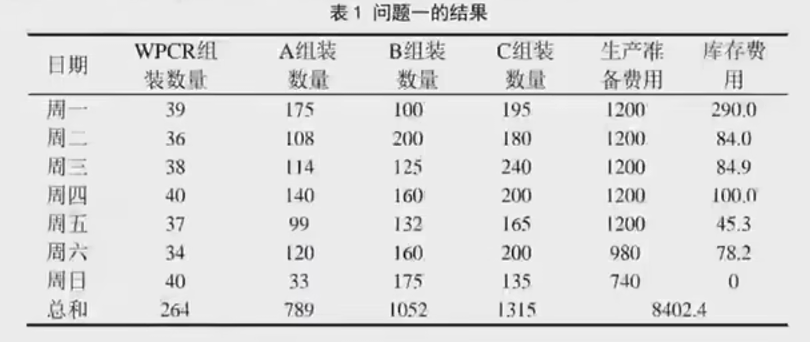
function [X,F]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C)
%初始化变量、计算目标函数值
flag1=0;
while flag1==0
X=[];
flag1=1;
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%第一天0库存
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的最小ABC需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
            flag2=1;
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=WPCR(i)-KC_WPCR(i-1);
        u=min(fix([x+KC(:,i-1)']./[A_x,B_x,C_x]));
    end
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=randi([s,u]);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
X=[SC_WPCR;SC];
X=reshape(X',1,28);
end
X1=[SC_WPCR;SC];%生产
X2=[KC_WPCR;KC];%库存
X1(find(X1>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=sum(X1.*[W(1);sum(W(2:5));sum(W(6:8));sum(W(9:12))],2);
f2=sum(X2.*C([1,2,6,9])',2);
F=sum(f1)+sum(f2);"

function J=jianyan1(X,WPCR,A_x,B_x,C_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=X(i,1);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0
    J=1;
else
    J=0;
end 

function [F,f1,f2]=fun1(X,WPCR,A_x,B_x,C_x,W,C)
%带入变量计算目标函数值
X=reshape(X',7,4);
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=X(i,1);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
X1=[SC_WPCR;SC];%生产
X2=[KC_WPCR;KC];%库存
X1(find(X1>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=sum(X1.*[W(1);sum(W(2:5));sum(W(6:8));sum(W(9:12))],1)';
f2=sum(X2.*C([1,2,6,9])',1)';
F=sum(f1)+sum(f2);

clear all
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
%每天总工时
T=[4500 2500 2750 2100 2500 2750 1500];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.95; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=1000; %颗粒总数，效果不好可以增加
X=[];
F=[];
for i=1:num
    [X(i,:),F(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
 for i=1:num
        [XX(i,:),FF(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan1(X,WPCR,A_x,B_x,C_x);
        if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0 | sum(x(1,:))<sum(WPCR) | J==1
            XX(i,:)=X(i,:);
        end
        %计算目标函数
        FF(i,1)=fun1(X(i,:),WPCR,A_x,B_x,C_x,W,C);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')
[~,f1,f2]=fun1(bestx,WPCR,A_x,B_x,C_x,W,C)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

6. 문제 2 모델의 이력서 및 솔루션

6.1 두 번째 문제 모델의 수립

6.1.1 작은 구성 요소가 큰 구성 요소를 조립

WPCR을 조립하려면 부품 A, B, C를 하루 전에 생산하여 창고에 넣어야 하며 부품 A1, A2, A3, B1, B2, C1, C2, C3도 생산하여 창고에 넣어야 합니다. 하루 전에 A, B, C를 조립합니다. 따라서 월요일에 구성품 주문 수요를 완료하려면 지난주 월요일 일요일에 필요한 대형 구성품 A, B, C를 조립해야 합니다. 그리고 지난 일요일에는 큰 부품을 조립하는 데 사용된 작은 부품을 마지막 토요일에 조립해야 합니다.
따라서 d일에 큰 부품을 조립하는 데 사용되는 작은 부품의 수는 d-1일에 조립된 작은 부품의 수와 d-1일에 남아 있는 작은 부품의 수를 합산해야 합니다. 따라서 공식 (5) 및 (6)은 다음과 같이 큰 성분의 제약 조건을 얻기 위해 수정됩니다.
$$MA{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MA1\_{}_{d-}+사1\_{}_{d-}}{6},\frac{MA2\_{}_{d-}+사2\_{}_{d-}}{8},\frac{MA3\_{}_{d-}+사3\_{}_{d-}}{2}\end{array}\right)\right]$$

$$엠비{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{메가바이트1_{d-}+SB{1}_{d-}}{2},\frac{메가바이트2_{d-}+SB{2}_{d-}}{4}\end{array}\right)\right]\text{\hspace{1em}( 22 )}$$

$$엠씨{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MC{1}_{d-}+SC{1}_{d-}}{8},\frac{MC{2}_{d-}+SC{2}_{d-}}{2},\frac{MC{3}_{d-}+SC{3}_{d-}}{12}\end{array}\right)\right]$$

6.1.2 남은 위젯

d일에 남아 있는 위젯의 수, 즉 저장해야 하는 위젯의 수는 두 부분으로 볼 수 있습니다. 한 부분은 d일에 조립된 작은 부품의 수이고 다른 부분은 d일에 조립된 큰 부품의 나머지 부분이며 나머지 부분은 d-1일에 조립된 작은 부품의 수와 d-1일에 남아 있는 작은 구성 요소 및 d일에 소비된 양을 뺀 값,

d일 남은 { d일에 조립된 수량 + (d일에 조립된 수량 - 1일에 조립된 수량 + d-1일에 남은 수량) - d일에 소비된 수량 d\begin{cases}일에 d일에 남은 조립 수량\\ +\ \ (d-1일 조립 수량 + d-1일 잔여 수량) - d일 소비 수량\end{cases}d 일 남음⎩ ⎨ ⎧d 일 에 조립된 수량+( 일 디-1 일 에 조립된 수량+디 _-1 일 남은 수량)-d 일 에 소비된 양

위젯의 나머지 부분은 다음과 같습니다.

$$사1\_{}_{}=MA1\_{}_{}+MA1\_{}_{d-}+사1\_{}_{d-}-6\times MA{\_}_{}$$
$$사2\_{}_{}=MA2\_{}_{}+MA2\_{}_{d-}+사2\_{}_{d-}-8\times MA{\_}_{}$$
$$사3\_{}_{}=MA3\_{}_{}+MA3\_{}_{d-}+사3\_{}_{d-}-2\times MA{\_}_{}$$
$$SB{1}_{}=메가바이트1_{}+메가바이트1_{d-}+SB{1}_{d-}-2\times 엠비{\_}_{}$$

$$SB{2}_{}=메가바이트2_{}+메가바이트2_{d-}+SB{2}_{d-}-4\times 엠비{\_}_{}\text{\hspace{1em}( 23 )}$$
$$SC{1}_{}=MC{1}_{}+MC{1}_{d-}+SC{1}_{d-}-8\times 엠씨{\_}_{}$$
$$SC{2}_{}=MC{2}_{}+MC{2}_{d-}+SC{2}_{d-}-2\times 엠씨{\_}_{}$$
$$SC{3}_{}=MC{3}_{}+MC{3}_{d-}+SC{3}_{d-}-12\times 엠씨{\_}_{}$$

6.1.3 로봇의 조립 수량은 나머지 대형 부품을 계산합니다.

로봇의 조립은 작은 부품을 큰 부품으로 조립하는 것과 동일하며, d일에는 d-1일의 어셈블리 또는 나머지 대형 부품을 사용하여 로봇을 조립합니다. 제약 조건은 다음과 같습니다.

$$남{\_}_{}⩽분\left[\left(\begin{array}{c}\frac{MA1\_{}_{d-}+사1\_{}_{d-}}{삼},\frac{메가바이트2_{d-}+SB{2}_{d-}}{4},\frac{MC{3}_{d-}+SC{3}_{d-}}{5}\end{array}\right)\right]\text{\hspace{1em}( 24 )}$$

다음과 같이 큰 구성 요소의 나머지 부분은 작은 구성 요소의 나머지 부분과 동일합니다.

$$사{\_}_{}=MA{\_}_{}+MA{\_}_{d-}+사{\_}_{d-}-삼\times 남{\_}_{}$$
$$에스비{\_}_{}=엠비{\_}_{}+엠비{\_}_{d-}+에스비{\_}_{d-}-4\times 남{\_}_{}\text{\hspace{1em}( 25 )}$$
$$에스{씨}_{}=엠씨{\_}_{}+엠씨{\_}_{d-}+에스{씨}_{d-}-5\times 남{\_}_{}$$

6.1.4 로봇 조립 수량 제약 및 잔여 계산

로봇의 조립 수량과 나머지는 다음과 같이 수정되지 않습니다.

$$남{\_}_{}+SW{\_}_{d-}⩾DW{\_}_{}\text{\hspace{1em}( 26 )}$$
$$SW{\_}_{}=엠씨{\_}_{}+남{\_}_{d-}+SW{\_}_{d-}-DW{\_}_{}\text{\hspace{1em}( 26 )}$$

6.1.5 다음날 생산 보장

다음주 월요일에 생산을 보장하려면 이번주말 일요일에 부품을 남겨둬야 하므로 질문 1의 식 (13)과 (14)는 고려하지 말아야 합니다. 다음 월요일을 8일로 간주하므로 8일에 조립된 로봇 수와 7일에 남은 로봇 수의 합계는 다음과 같이 다음 월요일 주문 수량 39보다 작아서는 안 됩니다.

$$남{\_}_{}+SW{\_}_{8-}⩾39\text{\hspace{1em}( 26 )}$$

이번 주에는 d일의 로봇 생산을 보장하기 위해 d일의 대형 부품 조립 수량과 d-1일의 소형 부품 조립 수량에 대한 제약 조건이 명확하지 않다는 점에 유의할 필요가 있습니다. 그러나 수학식 26에서는 d일에 로봇의 주문량(DW _d )과 d일에 제조되는 수량(MW _d )에 제약 이 있고 _d 일 에 대형 부품의 조립량에 제약이 있고, 식(22)에서 d-1일의 소형 부품 조립 수량에는 d일에 조립되는 대형 부품의 수에 대한 제약이 있습니다.

따라서 2일차에 생산되는 로봇의 수를 보장하기 위한 제약조건은 명시적으로 주어지지 않고 묵시적이다.

6.1.6 근로시간 제한

근무 시간 제한은 다음과 같이 수정되지 않습니다.
$$삼\times MA{\_}_{}+5\times 엠비{\_}_{}+5\times 엠씨{\_}_{}⩽{티}_{}\text{\hspace{1em}( 27 )}$$

6.1.7 목적 함수

목적 함수는 수정되지 않고 다음과 같이 문제 1과 동일합니다.
$$분C=\sum _{d=1}{아르\; 자형}_{}+\sum _{d=1}{에프}_{}\text{\hspace{1em}( 28 )}$$

6.2 두 번째 문제 모델의 솔루션

MATLAB을 사용하여 코드를 작성하여 두 번째 질문의 결과를 얻으십시오.

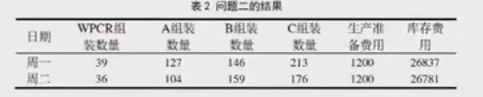
clear
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];
%每天总工时
T=[4500 2500 2750 2100 2500 2750 1500];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.95; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=1000; %颗粒总数
X=[];
F=[];
for i=1:num
    [X(i,:),F(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
 for i=1:num
        [XX(i,:),FF(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x);
        if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0 | sum(x(1,:))<sum(WPCR) | J==1
            XX(i,:)=X(i,:);
        end
        %计算目标函数
        FF(i,1)=fun2(X(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')
[~,f1,f2]=fun2(bestx,WPCR,A_x,B_x,C_x,W,C,D_x)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

function [X,F]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)
%初始化变量、计算目标函数值，小件提前两天，大件提前1天
flag1=0;
while flag1==0
X=[];
nn=2;%延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%假设第一天刚好满足WPCR
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的WPCR最小ABC需求量
        up=sub;
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
            flag2=1;
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=WPCR(i)-KC_WPCR(i+nn-1);
        u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
    end
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=randi([s,u]);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,28);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];%生产
X2=[SC_x(:,nn+1:end)];%生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];%库存ABC
X4=[KC_x(:,nn+1:end)];%库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function [F,f1,f2]=fun2(X,WPCR,A_x,B_x,C_x,W,C,D_x)
%初始化变量、计算目标函数值
X=reshape(X',7,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=X(i,1);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];%生产
X2=[SC_x(:,nn+1:end)];%生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];%库存ABC
X4=[KC_x(:,nn+1:end)];%库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=X(i,1);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0 | length(find(KC_x<0))>0
    J=1;
else
    J=0;
end

7. 문제 3모델의 수립 및 해결

7.1 세 번째 문제 모델의 수립

7.1.1 시간 변수의 결정

이 문제에서 시간은 7일에서 30주 210일로 변경되었으므로 시간변수는
$$디\in (-1,0,1,...,208,209,210)\text{\hspace{1em}( 29 )}$$

d=-1은 1주의 이전 주의 토요일이고 d=0은 1주의 이전 주의 일요일입니다. d=1은 30번째 주의 첫째 날인 첫 번째 주의 월요일이고, d=210은 30번째 주의 마지막 날인 30번째 주의 일요일입니다.

7.1.2 다운타임에 대한 0-1 변수

모델링에서 변수가 여러 정수 값을 가질 수 있는 문제가 발생하면 0-1 변수가 이진 변수라는 속성을 활용하여 0-1 변수 집합을 사용하여 변수를 대체할 수 있습니다. 따라서 이 속성 덕분에 다운타임 0-1 변수 하나를 대체하기 위해 0-1 변수 세트가 도입됩니다.

첫 번째 점검일을 예로 들면 첫 번째 점검일에 대한 모델은 다음과 같이 설정됩니다.

$$체크체크\_{\_}_{}=\{\begin{array}{ll}1& 내가점검해야\; 할날\\ & 당일\; 유지보수\end{array}\text{\hspace{1em}( 29 )}$$

위의 수식에서 첫 번째 수식은 0-1 변수로 첫 번째 유지 관리 날짜가 d번째 날인지 여부를 의미합니다. 첫 번째 유지 관리 날짜는 210일 중 하나만 될 수 있으므로, 즉 하루만 될 수 있으므로 위의 두 번째 공식은 제약 조건에 대해 도입됩니다.

1차 점검일의 구체적인 값을 쉽게 구할 수 있도록 0-1 변수가 2진 변수라는 특성 때문에 위의 공식에서 세 번째 공식을 도입하였다. 예를 들어, 1차 점검 날짜가 3일이면

$${나}_{}=1\text{\hspace{1em}( 31 )}$$
$${나}_{}={나}_{}={나}_{}=...={나}_{}={나}_{1(210}=0\text{\hspace{1em}( 31 )}$$

이때, 식(30)의 두 번째 식을 만족하였다.
그런 다음 (30)의 세 번째 공식은 다음과 같이 변환될 수 있습니다.
$$체크체크\_{\_}_{}=2^1{나는}_{}+2^2{나}_{}+...+2^{210}{나는}_{\left(1\right)}=2^1\times 0+2^2\times 0+2^{삼}\times 1+...+2^{210}\times 0=2^{삼}\text{\hspace{1em}( 31 )}$$

(30)의 네 번째 공식을 통해 다음과 같이 첫 번째 검사 날짜를 직접 구할 수 있습니다.
$$check데이터\_\_\_\_{}_{}=내가\_{\_}_2^{체크1\_\_}=내가\_{\_}_2^{(2^3}=삼\text{\hspace{1em}( 32 )}$$

따라서 7회 검사의 0-1 변수는 다음과 같이 얻습니다.

여기서 chechDate _t 는 t번째 검사의 특정 날짜입니다.

7.1.3 검사 간격

두 검사 날짜 사이에 6일의 간격을 더 편리하게 주기 위해 7개의 검사 순서를 먼저 제한합니다. 즉, checkDate _t 를 먼저 다음과 같이 정렬합니다.
$$chechDtei<chechDtei+1,나\in (1,2,\mathrm{3...5},6)\text{\hspace{1em}( 34 )}$$

정렬 후 두 검사 날짜 사이에 6일이라는 제약 조건이 다음과 같이 주어집니다.

$$chechDtei+6<chechDtei+1,나\in (1,2,\mathrm{3...5},6)\text{\hspace{1em}( 35 )}$$

7.1.4 총 작업 시간 제한 매트릭스 정의

이 질문의 생산 시간은 30주에 7일에서 210일로 변경되었으므로 총 근무 시간 제한 매트릭스를 재정의합니다.

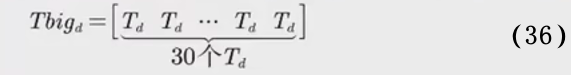
이 중 T _d 는 d 요일의 총 근무 시간 제한입니다.

따라서 총 인시 한도를 만족하는 제약 조건은 다음과 같습니다.

$$삼\times MAD\_+5\times 메가바이트+5\times 엠씨{\_}_{}⩽티가{지}_{}\text{\hspace{1em}( 37 )}$$

7.1.5 점검 후 총 근로시간 제한 완화

장비 점검 후 생산 능력이 향상되었으며 점검 첫 날 이후 총 생산 기한이 10%, 8%, ..., 2%, 0% 완화됩니다. 따라서 7회 점검의 구체적인 날짜가 확정된 후 점검 후 완화에 맞게 최대총인시한도 매트릭스의 값을 변경할 수 있다. 수식을 다음과 같이 변경합니다.

$$티가{지}_{(chehDate+offset}=티가{지}_{(chehDate+offset}\times (1+(0.1-0.02\times 오프설정\left)\right)\_\text{\hspace{1em}( 38 )}$$

$$오프설정\_\_\in (0,1,...4,5)$$

그 중 1, offset은 각 점검일로부터 역으로 상쇄되는 date offset이며, 각 offset마다 한도 완화가 2%씩 감소된다. 오프셋이 5배에 도달하면 한계 완화가 0%로 감소하고 오프셋이 중지됩니다.

7.1.6 검사 당일 부품 생산 불가

장비 유지보수 당일에는 부품을 생산할 수 없습니다. 즉, 유지보수일에 대형 부품, 소형 부품 및 로봇의 생산량이 0이므로 제약 조건은 다음과 같습니다.

$$MA1\_{}_{}=MA2\_{}_{}=MA3\_{}_{}=메가바이트1_{}=메가바이트2_{}=MC{1}_{}=MC{2}_{}=MC{3}_{}=0$$
$$MA{\_}_{}=엠비{\_}_{}=엠씨{\_}_{}=남{\_}_{}=0\text{\hspace{1em}( 39 )}$$
$$제이\in (체크체크데이터\_\_\_\_{\_}_{},티\in (1,2,...6,7))$$

7.1.7 생산을 계속할 수 있는지 확인

30주 210일이 끝난 후에도 주문 수요가 여전히 31번째 주 월요일, 즉 211일에 이행될 수 있도록 하기 위해 211일에 로봇의 생산 수량 MW와 나머지 210일째 로봇의 수량 SW11-은 211일째 이상이어야 하며, 하늘로봇의 수요량인 DW.1, 원칙은 6.1.5와 같다. 제약 조건은 다음과 같습니다.

$$남{\_}_{}+SW{\_}_{211-}⩾DW{\_}_{}\text{\hspace{1em}( 40 )}$$

이 질문은 211일 DW_{211}의 로봇 수요를 제공하지 않습니다. 여기에서 30주 월요일 데이터의 평균을 내고 반올림하여 DW ₂₁₁ =38을 얻습니다.

다른 제약 조건과 목적 함수는 문제 2의 모델에서 변경되지 않았으므로 여기서 반복하지 않습니다.

7.2 3-모델 문제의 해법

MATLAB을 사용하여 코드를 작성하여 질문 3의 결과를 얻으십시오.

clear
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40
39 33 37 43 34 30 39
42 36 35 38 36 35 41
38 36 36 48 34 35 39
38 36 40 40 40 34 39
40 30 36 40 34 36 37
41 36 41 41 38 29 43
33 31 40 42 42 30 40
35 36 38 33 35 37 41
43 35 42 37 36 33 39
38 32 41 36 40 31 34
37 37 41 39 38 35 38
38 38 33 42 42 29 33
39 37 44 38 35 36 38
40 39 38 38 37 34 44
35 36 38 39 39 39 39
43 28 39 41 38 30 38
35 37 40 41 40 35 41
36 35 40 41 37 38 36
37 38 39 41 38 37 44
37 37 37 36 39 33 41
39 37 42 37 36 28 43
40 32 35 45 40 34 43
38 36 37 36 40 28 45
38 40 38 36 35 40 42
31 31 44 36 31 36 40
40 36 34 43 35 32 39
33 33 36 41 34 38 40
35 34 37 37 39 36 40
37 41 39 41 36 32 44];
WPCR=reshape(WPCR',210,1)';
WPCR=[WPCR,WPCR(1:2)];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];
%每天总工时
T=repmat([4500 2500 2750 2100 2500 2750 1500],1,30);
T=[T(end),T,T(1)];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.9; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=2; %颗粒总数
X=[];
A=[];
F=[];
for i=1:num
    [X(i,:),A(i,:),F(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
bestA=A(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
    AA=[];
 for i=1:num
        [XX(i,:),AA(i,:),FF(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
            A(i,:)=AA(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
                A(i,:)=AA(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        %粒子群算法限制最多找10次位置
        m=1;
        flag=0;
        while flag==1
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan3(x,AA(i,:),WPCR,A_x,B_x,C_x);
        if (length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))==0 & sum(x(1,:))>=sum(WPCR) & J==0) | m==10
            XX(i,:)=X(i,:);
        else
            m=m+1;
        end
        end
        %计算目标函数
        FF(i,1)=fun3(XX(i,:),AA(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
            A(i,:)=AA(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
        bestA=A(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('停检时间')
disp(bestA)
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量，见工作区矩阵zz')
x=reshape(bestx',212,4);
zz=[x(1:210,1),x(2:211,2:4)];
disp('生产准备费用、库存费用见工作区矩阵f1、f2')
[~,f1,f2]=fun3(bestx,bestA,WPCR,A_x,B_x,C_x,W,C,D_x);
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

function [X,b,F]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)
%初始化变量、计算目标函数值，小件提前两天，大件提前1天
flag1=0;
while flag1==0
%检修
flag3=0;
while flag3==0
    A=zeros(1,length(WPCR));
    a=10+randperm(length(WPCR)-20);
    aa=a(1:7);
    A(aa)=1;
    b=find(A==1);
    c=b(2:end)-b(1:end-1);
    d=find(c<6);
    if length(d)==0
        flag3=1;
    end
end
%检修后提高效率
AA=[];%对应的时间
for i=1:length(b)
    AA=[AA,b(i)+1:b(i)+5];
end
G=repmat([1.1 1.08 1.06 10.4 1.02],1,length(b));
TT=T;
TT(AA)=TT(AA).*G;
X=[];
nn=2;%延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%假设第一天刚好满足WPCR
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的WPCR最小ABC需求量
        up=sub;
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])*2).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if i==1
            flag2=1;
        elseif i>1
            if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
                flag2=1;
            end
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=max(WPCR(i)-KC_WPCR(i+nn-1),0);
        u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
    end
    if u<s
        flag1=0;
        continue
    end
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=randi([s,u]);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,848);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];%生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];%库存ABC
X4=[KC_x(:,nn+1:end-2)];%库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function [F,f1,f2]=fun3(X,b,WPCR,A_x,B_x,C_x,W,C,D_x)
%初始化变量、计算目标函数值
X=reshape(X',212,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];%生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];%库存ABC
X4=[KC_x(:,nn+1:end-2)];%库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function J=jianyan3(X,b,WPCR,A_x,B_x,C_x,D_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0 | length(find(KC_x<0))>0
    J=1;
else
    J=0;
end

8. 네 번째 문제 모델의 수립 및 해결

8.1 문제의 네 가지 모델 설정

8.1.1 데이터 분석

이 질문은 31주차 로봇의 사용수요를 예측할 필요가 있습니다.질문에서 주어진 데이터 분석에 따르면 데이터의 변동은 일정한 주기성을 가지며 기간 시계열 데이터입니다.종속변수는 단 하나: 사용된 로봇의 수. 그런 다음 사용된 로봇의 수를 종속변수로 하여 일변량 시계열 분석을 기반으로 한 로봇 수요 예측 모델을 설정합니다.

시간 변수로 주가 있는 데이터는 특정 기간을 제공하지 않으므로 데이터를 훈련 그룹과 실험 그룹으로 나누고 다른 기간 길이를 사용하여 훈련 그룹을 모델링하고 Q 테스트를 통과한 모델을 선별하고 그런 다음 실험 그룹의 데이터를 사용하여 어떤 모델이 가장 잘 예측하는지 결정합니다. 예측 오차가 가장 작은 모델을 선택하고 모든 데이터를 사용하여 리모델링하고 미래 데이터에 대해 예측합니다. 마지막으로 예측된 ​​추세가 합리적인지 판단하기 위해 예측된 시계열 다이어그램을 그립니다.

8.1.2 데이터 전처리

30주 201일 동안 누락된 데이터 없이 데이터를 관찰합니다. 시간 변수를 주 단위로 정의하고 시간을 가로축으로, 로봇 수를 세로축으로 하여 시계열 그래프를 그립니다. 시계열 그래프를 분석하여 추세나 계절성 없이 데이터가 특정 범위 내에서 위아래로 변동함을 찾습니다.

8.1.3 일변량 시계열 기반 예측 모델 구축

훈련 그룹 데이터는 사이클 길이가 7인 시퀀스로 SPSS 전문 모델러를 이용하여 최적의 시계열 분석 모델을 구축하였다. Expert Modeler는 각 종속 시퀀스에 가장 적합한 모델을 자동으로 찾습니다. 독립(예측자) 변수가 지정되면 전문 모델러는 ARIMA 모델의 내용에 대해 종속 계열과 통계적으로 유의한 관계가 있는 모델을 선택합니다. 모델 변수는 적절하게 차이 또는 제곱근 또는 자연 로그 변환을 사용하여 변환되었습니다. 기본적으로 Expert Modeler는 지수 평활 및 ARIMA 모델을 모두 고려합니다. 그러나 ARIMA 모델만 검색하거나 지수 평활 모델만 검색하도록 Expert Modeler를 제한할 수도 있습니다. 이상값의 자동 감지를 지정할 수도 있습니다.

sPSS Expert Modeler는 자동으로 최적의 모델인 단순 계절 모델을 선택했습니다.

8.1.4 예측 모델 테스트

모델이 완전히 인식되는지 확인: 시계열 모델을 추정한 후 잔차에 대한 백색 잡음 테스트를 수행해야 하며, 잔차가 백색 잡음이면 선택한 모델이 시계열의 법칙을 완전히 식별할 수 있음을 의미 , 즉, 모델이 허용 가능합니다. ; 잔차가 백색 잡음이 아닌 경우 모델에서 인식하지 못하는 정보가 아직 남아 있으면 제거됩니다.

ACF 자기상관 계수와 PACF 편자기상관 함수는 잔차가 백색잡음인지, 즉 시계열이 모델에서 완전히 인식될 수 있는지 여부를 결정하는 데 도움이 될 수 있습니다.

위의 표에서 알 수 있듯이 잔차에 대한 Q-검정을 통해 얻은 p 값은 0.451입니다. 즉, 귀무가설을 기각할 수 없고 잔차가 백색잡음 시퀀스라고 생각하므로 단순 계절 모델이 잘 될 수 있습니다. 이 질문에서 로봇을 식별하십시오. 수요 데이터.

모델 비교 및 ​​선택: 고정 R ² 또는 AIC 및 BIC 기준을 사용합니다. R ² 는 선형 모델 피팅의 품질을 반영하는 데 사용할 수 있습니다. 1에 가까울수록 피팅이 더 정확합니다. 더 많은 매개변수가 추가될수록 모델 피팅 효과는 더 좋아지지만, 이는 모델의 복잡성을 증가시키는 대가를 치르게 됩니다(과적합 문제). 따라서 모델 선택은 모델 복잡성과 데이터를 해석하는 모델의 능력 간의 최상의 균형을 추구합니다. BIC는 모델의 복잡성에 대한 페널티 계수가 더 크기 때문에 AIC가 선택한 모델보다 BIC가 더 간결한 경우가 많으므로 작은 R ² 및 BIC를 모델 선택 매개변수로 선택하는 원칙입니다.

BIC(Bayesian Information Criterion) 표현식은 다음과 같습니다.

$$BIC=ln\left(T\right)(모델의\; 매개변수\; 수)-2ln(모델의\; 최대\; 가능도\; 함수)\text{\hspace{1em}( 41 )}$$

31주차: 38, 35, 39, 40, 37, 34, 40에 대한 예측 값을 가져옵니다. 주 32: 38, 35의 처음 2일에 대한 예측 값. 따라서 다음과 같이 미래의 d번째 날에 로봇 수요량 행렬을 구합니다.
$$DWpredict=[38,35,39,40,37,34,40,38,35]\text{\hspace{1em}( 42 )}$$

8.1.5 매일 정상 배송 보장

일일 로봇 주문이 95% 이상의 확률로 배송되도록 보장하기 위해 조립 로봇 수에 대한 제약을 다음과 같이 수정합니다.

$$남{\_}_{}+SW{\_}_{d-}⩾DW{\_}_{미리보기\_\_\_\_{}_{}}\times 0.95\text{\hspace{1em}( 43 )}$$

8.1.6 일주일 내내 정상적인 배송 보장

일주일 내내 로봇 주문이 85% 이상의 확률로 배송될 수 있도록 하기 위해 다음과 같은 제약이 있습니다.

$$\sum _{d=1}남{\_}_{}⩾0.85\times \sum _{d=1}DWpredic{t}_{}\text{\hspace{1em}( 44 )}$$
일일 주문은 95% 이상의 확률로 배송되었고, 일주일 전체의 로봇 주문은 85% 이상의 확률로 배송되어야 한다는 점, 즉 수학식 44 식(43)에 함축되어 있다. 따라서 매일 정상적인 배송을 보장하는 것으로 충분합니다. 즉, 공식 (43)은 무시할 수 있습니다.

Nine, 공식 표준 답변

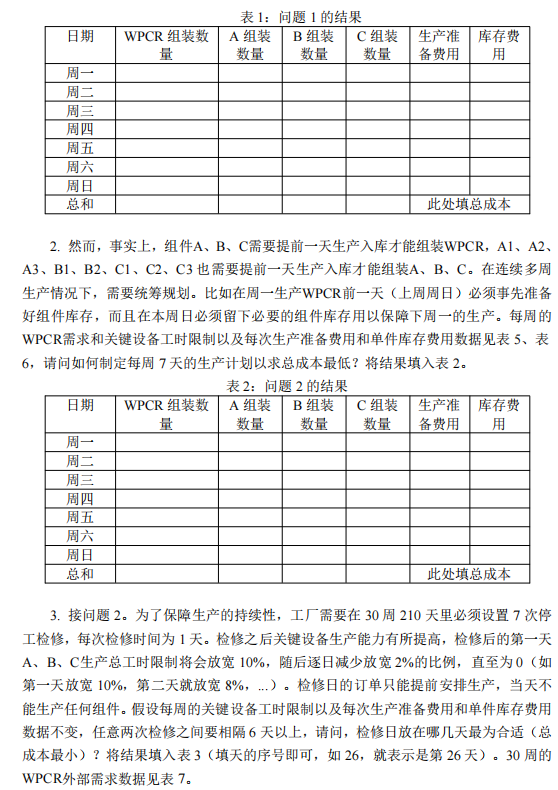
1. 첫 번째 질문의 최종 결과

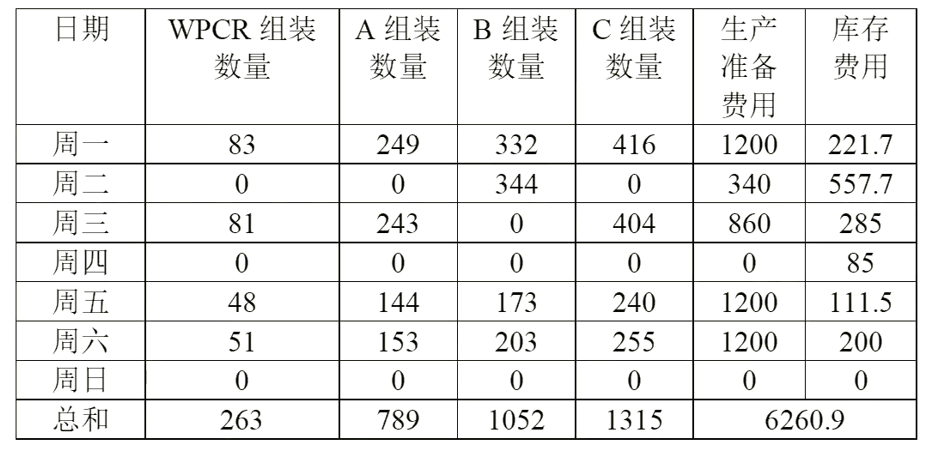
2. 두 번째 질문의 최종 결과

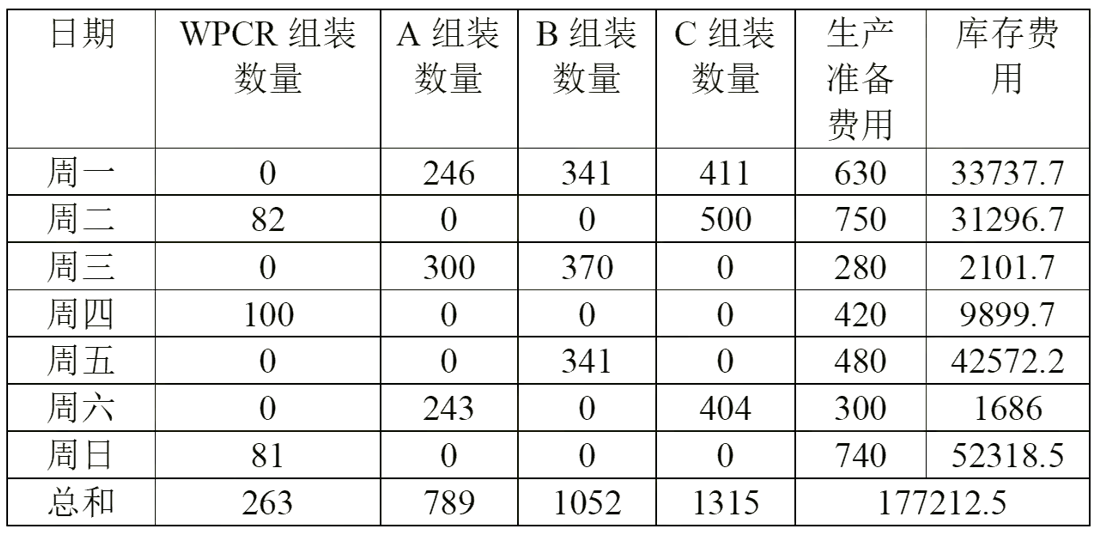
3. 세 번째 질문의 최종 결과

4. 네 번째 질문의 최종 결과