ChatGPT 강화 학습 빅 킬러 - 근접 전략 최적화(PPO)

ChatGPT 강화 학습 빅 킬러 - 근접 전략 최적화(PPO)

Proximal Policy Optimization ( Proximal Policy Optimization )은 현재 가장 발전된 강화 학습(RL) 알고리즘인 Proximal Policy Optimization Algorithms (Schulman et. al., 2017) 논문 에서 유래되었습니다. 이 우아한 알고리즘은 다양한 작업에 사용할 수 있으며 많은 프로젝트에 적용되었으며 최근 인기있는 ChatGPT가 이 알고리즘을 채택했습니다.

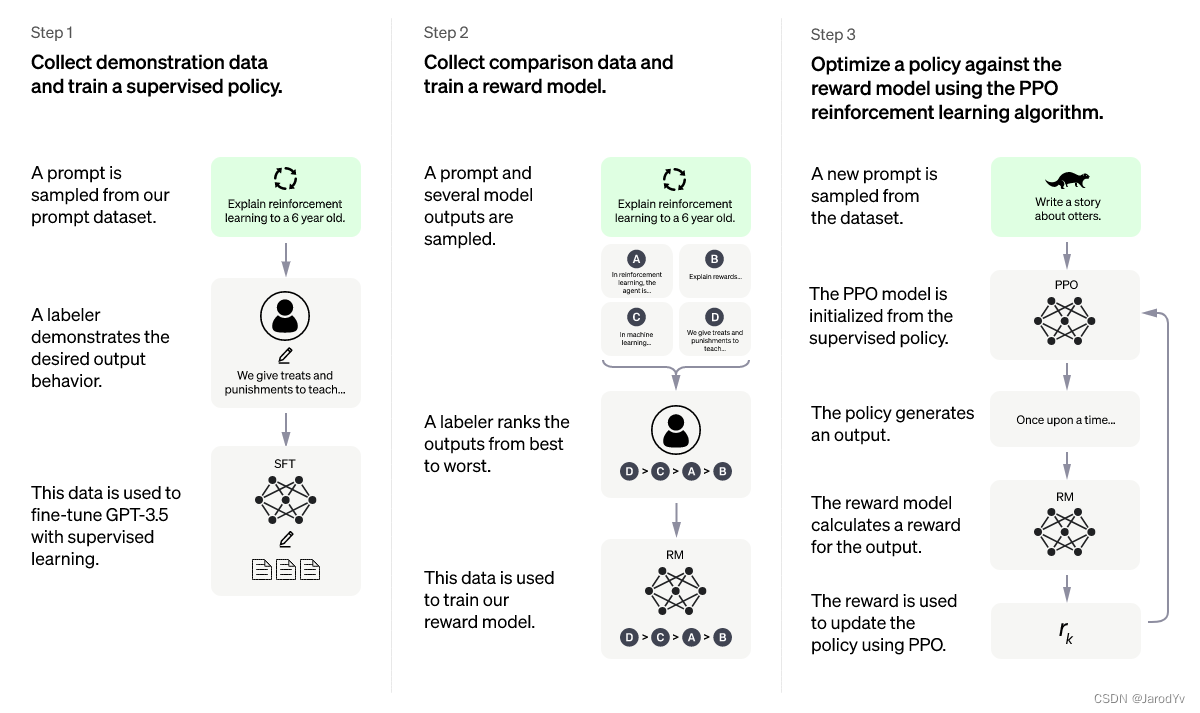
ChatGPT 알고리즘과 학습 과정을 설명하는 글은 인터넷에 많이 있지만 핵심 근접 전략 최적화 알고리즘에 대해 깊이 있게 설명하는 사람은 많지 않습니다.

강화 학습

고급 강화 학습 알고리즘인 근접 전략 최적화에는 강화 학습에 대한 이해가 필요합니다. 강화학습에 대한 글은 많이 있는데 여기서는 많이 소개하지 않겠지만 ChatGPT가 어떻게 설명하는지 볼 수 있습니다.

ChatGPT에서 제공하는 설명은 비교적 이해하기 쉬우며 학문적으로 강화 학습 과정은 다음과 같습니다.

강화 학습 프레임워크

위 그림에서 환경은 매 순간 에이전트 에게 보상을 피드백 하고 현재 상태를 모니터링합니다. 이 정보를 통해 에이전트는 환경에서 조치를 취한 다음 새로운 보상, 상태 등이 에이전트에 피드백되어 루프를 형성합니다. 이 프레임워크는 매우 일반적이며 다양한 분야에 적용될 수 있습니다.

우리의 목표는 보상을 극대화하는 에이전트를 만드는 것입니다. 일반적으로 이 최대화 보상은 개별 시간 할인 보상의 합계입니다.
$$G=\sum _{티=0}{씨}^{티르}{\_}_{}$$
여기서 $\gamma$ 는 일반적으로 [0.95, 0.99], rt r_t범위의 할인 계수입니다.${아르\; 자형}_{}$시간 t에서의 보상입니다.

연산

그렇다면 강화 학습 문제를 어떻게 해결할 수 있을까요? (Markov 의사 결정 프로세스 또는 MDP의 경우) 모델 기반 (환경 모델 생성) 및 모델 프리 (주어진 상태에서만 학습)의 두 가지 범주로 분류될 수 있는 다양한 알고리즘이 있습니다 .

강화 학습 알고리즘의 분류

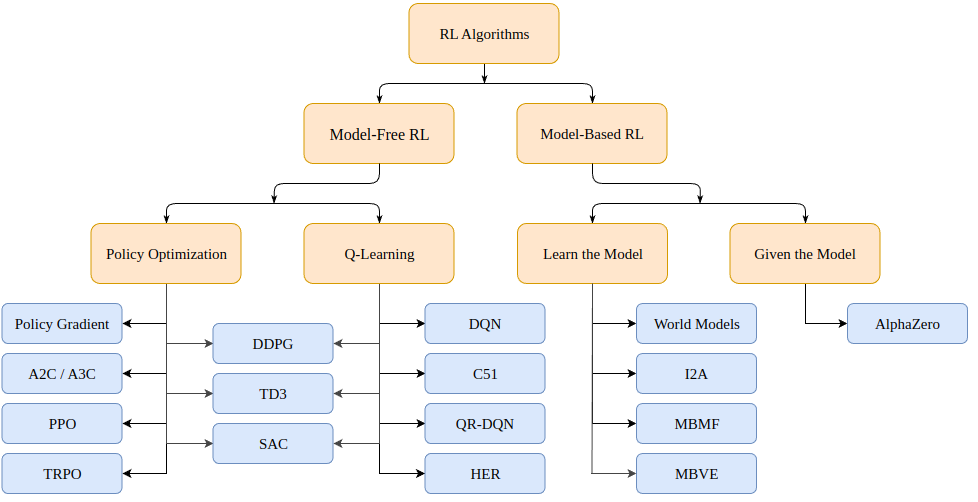
모델 기반 알고리즘은 환경 모델을 생성하고 해당 모델을 사용하여 미래 상태 및 보상을 예측합니다. 모델은 주어지거나(예: 체스판) 학습됩니다.

모델이 없는 알고리즘은 교육 중에 발생한 상태(정책 최적화 또는 PO)에 대해 조치를 취하는 방법과 좋은 보상을 제공하는 상태 조치(Q-Learning)를 직접 학습합니다.

오늘 논의할 근접 정책 최적화 알고리즘은 PO 알고리즘 계열에 속합니다. 따라서 학습을 촉진하기 위해 환경 모델이 필요하지 않습니다. PO와 Q-Learning 알고리즘의 주요 차이점은 PO 알고리즘은 연속적인 행동 공간(즉, 우리의 행동이 참 값을 가짐)이 있는 환경에서 사용할 수 있고 최적의 전략을 찾을 수 있지만 Q-Learning 알고리즘은 둘 다 할 수 없다는 것입니다. 이것이 PO 알고리즘이 더 인기 있는 또 다른 이유입니다. 반면에 Q-Learning 알고리즘은 더 단순하고 직관적이며 훈련하기 쉬운 경향이 있습니다.

정책 최적화(기울기 기반)

정책 최적화 알고리즘은 정책을 직접 학습할 수 있습니다. 이를 위해 정책 최적화는 유전 알고리즘과 같은 기울기가 없는 알고리즘 또는 더 일반적인 기울기 기반 알고리즘을 사용할 수 있습니다.

그래디언트 기반 방법은 누적 보상과 관련하여 학습된 정책의 그래디언트를 추정하려는 모든 방법을 의미합니다. 이 그래디언트(또는 그 근사치)를 알고 있으면 정책의 매개변수를 그래디언트 방향으로 이동하여 보상을 최대화할 수 있습니다.

정책 기울기 방법은 기울기 $g:={\nabla }_{}그리고\left[{\sum }_{티=0}^{}{아르\; 자형}_{}\right]$ 예상 총 보상을 최대화합니다. 다음과 같은 형식의 정책 기울기에 대한 몇 가지 다른 관련 표현식이 있습니다.

$$g=그리고[\sum _{티=0}{추신}_{}{\nabla }_{}로지파이\_\_{}_{}({\_}_{}|{에스}_{})]\text{\hspace{1em}( 1 )}$$

여기서 ${추신}_{}$다음과 같을 수 있습니다.

1. ${\sum }_{티=0}^{}{아르\; 자형}_{}$: 궤적의 총 보상
2. ${\sum }_{{티}^{\prime }=t}^{}{아르\; 자형}_{{티}^{}}$: a_t에서 다음 작업${ㅏ}_{}$보상
3. ${\sum }_{티=0}^{}{아르\; 자형}_{}-b\left({들}_{}\right)$ : 위 수식의 기본 버전
4. ${큐}^{\pi }(s_{},{ㅏ}_{})$ : 상태-행동 가치 함수
5. ${ㅏ}^{\pi }(s_{},{ㅏ}_{})$ : 어드밴티지 함수
6. ${아르\; 자형}_{}+{안에}^{\pi }\left(s_{티+}\right)+{안에}^{\pi }\left(s_{}\right)$ : TD 잔차

다음 세 공식의 구체적인 정의는 다음과 같습니다
$$\begin{gathered} {안에}^{\pi }\left(s_{}\right):={그리고}_{{에스}_{t+1:},{\_}_{t:}}\left[\sum _{내가=0}{아르\; 자형}_{티+}\right] \\ {큐}^{\pi }(s_{},{ㅏ}_{}):={그리고}_{{에스}_{t+1:},{\_}_{t+1:}}\left[\sum _{내가=0}{아르\; 자형}_{티+}\right]\text{\hspace{1em}( 2 )} \end{gathered}$$

$${ㅏ}^{\pi }(s_{},{ㅏ}_{}):={큐}^{\pi }(s_{},{ㅏ}_{})-{안에}^{\pi }\left(s_{}\right)\text{\hspace{1em}( 3 )}$$

그래디언트를 추정하는 방법에는 여러 가지가 있습니다. 여기에서 총 보상, 후속 조치의 보상, 기본 버전을 뺀 보상, 상태-행동 가치 함수, 우세 함수(원본 PPO 논문에서 사용됨) 및 시간 차이( TD) 잔여 차이. 이 값을 최대화 목표로 선택할 수 있습니다. 원칙적으로 둘 다 우리가 관심을 갖는 실제 그래디언트의 추정치를 제공합니다.

근접 전략 최적화

근접 정책 최적화(Proximal Policy Optimization, 줄여서 PPO)는 정책 최적화 그래디언트를 기반으로 하는 (모델이 없는) 알고리즘입니다. 알고리즘은 훈련 중 경험을 바탕으로 얻은 누적 보상을 최대화하는 정책을 학습하는 것을 목표로 합니다.

행위자 π θ ( . ∣ st ) \pi\theta(. \mid st ) $\pi \theta (.\_|st)$ 및비평가 (비평) $V\left(st\right)조성$ . 전자는 시간tt해당 상태에 대한 예상 누적 보상(스칼라)을 추정하는$t\; 에서\; 다음\; 작업의\; 확률\; 분포를\; 출력합니다.$액터와 비평가 모두 상태를 입력으로 사용하기 때문에 상위 수준 기능을 추출하기 위해 두 네트워크 간에 백본 아키텍처를 공유할 수 있습니다.

PPO는 정책이 더 높은 "장점", 즉 평가자가 예측한 것보다 훨씬 더 높은 누적 보상을 가진 조치를 선택하도록 하는 것을 목표로 합니다. 동시에 최적화 문제를 일으킬 수 있는 너무 많은 전략을 한 번에 업데이트하고 싶지 않습니다. 마지막으로 정책의 엔트로피가 높으면 더 많은 탐색을 장려하기 위해 추가 보상을 제공하는 경향이 있습니다.

총 손실 함수는 CLIP 항, 가치 함수(VF) 항 및 엔트로피 보상 항의 세 가지 항으로 구성됩니다. 최종 목표는 다음과 같습니다.
$${엘}_{티}^{CLIP+VF+}\left(나는\right)={\stackrel{^^}{그리고}}_{}\left[{패}_{티}^{클리피\_}\right(나는)-{씨}_{}{엘}_{티}^{브이}(나는)+{씨}_{}S[{\pi }_{}\left]\right({초}_{}\left)\right]$$
여기서${씨}_{}$및 ${씨}_{}$정책 평가(비평) 및 탐색(탐색) 정확도의 중요성을 각각 측정하는 하이퍼파라미터입니다.

CLIP 항목

우리가 말했듯이, 손실 함수는 행동 확률의 최대화(또는 최소화)를 유발하며, 이는 행동 긍정적 이점(또는 부정적 이점)으로 이어집니다
$${엘}^{CLIP}\left(\theta \right)={\stackrel{^^}{그리고}}_{}\left[내\right(r_{}\left(나는\right){ㅏ}_{},클립ip(r\_{}_{}(나는),1-ϵ,1+)\_{\stackrel{^^}{ㅏ}}_{}\left)\right]$$
열기:
$${아르\; 자형}_{}\left(나는\right)=\frac{{파이}_{}({\_}_{}|{에스}_{}}{{파이}_{{나}_{올디\_}}({\_}_{}|{에스}_{})}$$
이전과 비교하여 이전 작업을 수행할 가능성이 현재(업데이트된 정책) 얼마나 되는지 측정하는 비율입니다. 원칙적으로 우리는 이 계수가 너무 커지는 것을 원하지 않습니다. 너무 크면 전략이 갑자기 바뀌는 것을 의미하기 때문입니다. 그래서 최소 합 $[1-ϵ,1+ϵ]$ , 여기서$ϵ$ 는 하이퍼파라미터입니다.

어드밴티지 계산 공식은 다음과 같습니다 .
$${\stackrel{^^}{ㅏ}}_{}=-V(s\_{}_{})+{아르\; 자형}_{}+\gamma r{\_}_{티+}+{씨}^{2r}{\_}_{t+}+\cdots +{씨}^{(티-티+1)}{r}_{티-}+{씨}^{티-티}V\left({초}_{}\right)$$
여기서:${ㅏ}_{}$추정된 이점, $-V(s\_{}_{})$ 는 추정된 초기 상태 값,${씨}^{티-티}V\left({초}_{}\right)$ 는 추정된 최종 상태 값이고 중간 부분은 프로세스 동안 관찰된 누적 보상입니다.

주어진 상태 st s_t 에 대한 평가자의 응답을 단순히 측정한다는 것을 알 수 있습니다.${에스}_{}$오류 정도. 더 높은 누적 보상을 받으면 배당률 추정치는 양수가 되고 이 상태에서 행동할 가능성이 높아집니다. 그 반대의 경우도 마찬가지입니다. 더 높은 보상을 기대하지만 더 작은 보상을 받는 경우 배당률 추정치는 음수가 되며 이 단계에서 조치를 취할 가능성이 줄어듭니다.

우리가 최종 상태 s T s_T 까지 가는 경우에 유의하십시오.${에스}_{}$, 우리는 더 이상 평가자에게 의존할 필요가 없으며 단순히 평가자와 실제 누적 보상을 비교할 수 있습니다. 이 경우 이점의 추정치가 실제 이점입니다.

가치 함수 항

어드밴티지를 잘 예측하려면 주어진 상태의 가치를 예측할 수 있는 평가자가 필요합니다. 이 모델은 간단한 MSE 손실이 있는 지도 학습입니다
$${엘}_{티}^{브이}=MSE(r_{}+\gamma r{\_}_{티+}+\cdots +{씨}^{(티-티+1)}{r}_{티-}+브이({초}_{}),브이({초}_{}))=||{\stackrel{^^}{ㅏ}}_{}|{|}_{}$$
반복할 때마다 평가자를 업데이트하여 교육이 진행됨에 따라 점점 더 정확한 상태 값을 제공합니다.

엔트로피 보상 기간

마지막으로 정책 출력 분포의 엔트로피에 대한 작은 보상 탐색을 권장합니다. 표준 엔트로피는 다음과 같습니다.
$$S\left[{\pi }_{}\right]\left({초}_{}\right)=-\int {파이}_{}({\_}_{}|{에스}_{}\left)로그\right(피\_\_{}_{}({\_}_{}|{에스}_{}\left)\right){\_}_{}$$

알고리즘 구현

위의 설명이 명확하지 않더라도 걱정하지 마십시오. 다음은 근접 전략 최적화 알고리즘을 처음부터 단계별로 구현하는 방법입니다.

도구 코드

먼저 필요한 라이브러리를 가져옵니다.

from argparse import ArgumentParser

import gym
import numpy as np
import wandb

import torch
import torch.nn as nn
from torch.optim import Adam
from torch.optim.lr_scheduler import LinearLR
from torch.distributions.categorical import Categorical

import pytorch_lightning as pl

PPO의 중요한 하이퍼파라미터는 행위자 수, 수평선, 엡실론, 각 최적화 단계의 에포크 수, 학습률, 할인 계수 감마, 다양한 손실 항목을 평가하기 위한 상수 c1 및 c2입니다. 매개변수를 통해 이러한 하이퍼 매개변수를 전달합니다.

def parse_args():
    """解析参数"""
    parser = ArgumentParser()

    parser.add_argument("--max_iterations", type=int, help="训练迭代次数", default=100)
    parser.add_argument("--n_actors", type=int, help="actor数量", default=8)
    parser.add_argument("--horizon", type=int, help="每个actor的时间戳数量", default=128)
    parser.add_argument("--epsilon", type=float, help="Epsilon", default=0.1)
    parser.add_argument("--n_epochs", type=int, help="每次迭代的训练轮数", default=3)
    parser.add_argument("--batch_size", type=int, help="Batch size", default=32 * 8)
    parser.add_argument("--lr", type=float, help="学习率", default=2.5 * 1e-4)
    parser.add_argument("--gamma", type=float, help="折扣因子gamma", default=0.99)
    parser.add_argument("--c1", type=float, help="损失函数价值函数的权重", default=1)
    parser.add_argument("--c2", type=float, help="损失函数熵奖励的权重", default=0.01)
    parser.add_argument("--n_test_episodes", type=int, help="Number of episodes to render", default=5)
    parser.add_argument("--seed", type=int, help="随机种子", default=0)

    return vars(parser.parse_args())

기본적으로 매개변수는 백서에 설명된 대로 설정됩니다. 이상적으로 우리의 코드는 가능한 한 GPU에서 실행되어야 하므로 Torch의 장비를 설정해야 합니다.

def get_device():
    if torch.cuda.is_available():
        device = torch.device("cuda")
        print(f"Found GPU device: {
      
      torch.cuda.get_device_name(device)}")
    else:
        device = torch.device("cpu")
        print("No GPU found: Running on CPU")
    return device

강화 학습을 수행할 때 일반적으로 모델을 업데이트하는 데 사용되는 현재 모델에서 발생한 상태, 작업 및 보상을 저장하기 위해 버퍼를 설정합니다. run_timestamps주어진 환경에서 주어진 모델을 실행하고 고정된 수의 타임스탬프를 얻는 함수를 만듭니다 (에피소드가 끝나면 환경 재설정). render=False또한 이 옵션을 사용하여 훈련된 모델의 성능만 확인하려고 합니다.

@torch.no_grad()
def run_timestamps(env, model, timestamps=128, render=False, device="cpu"):
    """针对给定数量的时间戳在给定环境中运行给定策略。 
    返回具有状态、动作和奖励的缓冲区。"""
    buffer = []
    state = env.reset()[0]

    # 运行时间戳并收集状态、动作、奖励和终止
    for ts in range(timestamps):
        model_input = torch.from_numpy(state).unsqueeze(0).to(device).float()
        action, action_logits, value = model(model_input)
        new_state, reward, terminated, truncated, info = env.step(action.item())

        # (s, a, r, t)渲染到环境或存储到buffer
        if render:
            env.render()
        else:
            buffer.append([model_input, action, action_logits, value, reward, terminated or truncated])

        # 更新当前状态
        state = new_state

        # 如果episode终止或被截断，则重置环境
        if terminated or truncated:
            state = env.reset()[0]

    return buffer

이 함수의 반환 값(렌더링되지 않은 경우)은 상태, 수행된 작업, 작업 확률(로짓), 평가자 값, 보상 및 각 타임스탬프에서 제공되는 정책의 최종 상태를 포함하는 버퍼입니다. 이 함수는 데코레이터를 사용하므로 @torch.no_grad()환경과 상호 작용하는 동안 수행되는 작업에 대한 그래디언트를 저장할 필요가 없습니다.

핵심 코드

위의 도구 기능을 통해 근접 전략 최적화의 핵심 코드를 개발할 수 있습니다. 먼저 새로운 기본 기능 프로세스를 만듭니다.

def main():
    # 解析参数
    args = parse_args()
    print(args)

    # 设置种子
    pl.seed_everything(args["seed"])

    # 获取设备
    device = get_device()

    # 创建环境
    env_name = "CartPole-v1"
    env = gym.make(env_name)

    # TODO 创建模型，训练模型，输出结果
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
    training_loop(env, model, args)
    model = load_best_model()
    testing_loop(env, model)

위는 전체 프로그램의 프로세스 프레임워크입니다. 다음으로 PPO 모델, 학습 및 테스트 기능을 정의하기만 하면 됩니다.

PPO 모델의 아키텍처는 여기에서 자세히 설명하지 않으며 환경에서 작동하는 두 가지 모델(배우 및 비평가)만 필요합니다. 물론 모델 아키텍처는 더 복잡한 작업에서 중요한 역할을 하지만 간단한 작업에서는 MLP가 그 일을 할 수 있습니다.

따라서 배우와 비평가 모델을 포함하는 MyPPO클래스를 . 일부 상태에서 전달 방법을 실행할 때 행위자의 샘플링된 행동, 가능한 각 행동의 상대적 확률(로짓) 및 각 상태에 대한 비평가의 추정치를 반환합니다.

class MyPPO(nn.Module):
    """
    PPO模型的实现。 
    相同的代码结构即可用于actor，也可用于critic。
    """

    def __init__(self, in_shape, n_actions, hidden_d=100, share_backbone=False):
        # 父类构造函数
        super(MyPPO, self).__init__()

        # 属性
        self.in_shape = in_shape
        self.n_actions = n_actions
        self.hidden_d = hidden_d
        self.share_backbone = share_backbone

        # 共享策略主干和价值函数
        in_dim = np.prod(in_shape)

        def to_features():
            return nn.Sequential(
                nn.Flatten(),
                nn.Linear(in_dim, hidden_d),
                nn.ReLU(),
                nn.Linear(hidden_d, hidden_d),
                nn.ReLU()
            )

        self.backbone = to_features() if self.share_backbone else nn.Identity()

        # State action function
        self.actor = nn.Sequential(
            nn.Identity() if self.share_backbone else to_features(),
            nn.Linear(hidden_d, hidden_d),
            nn.ReLU(),
            nn.Linear(hidden_d, n_actions),
            nn.Softmax(dim=-1)
        )

        # Value function
        self.critic = nn.Sequential(
            nn.Identity() if self.share_backbone else to_features(),
            nn.Linear(hidden_d, hidden_d),
            nn.ReLU(),
            nn.Linear(hidden_d, 1)
        )

    def forward(self, x):
        features = self.backbone(x)
        action = self.actor(features)
        value = self.critic(features)
        return Categorical(action).sample(), action, value

Categorical(action).sample()하나의 행동(각 상태에 대해)에 대한 행동 로짓 및 샘플을 사용하여 범주형 분포가 생성된다는 점에 유의하십시오 .

마지막으로 training_loop함수 . 논문에서 알 수 있듯이 함수의 실제 서명은 다음과 같아야 합니다.

def training_loop(env, model, max_iterations, n_actors, horizon, gamma, 
epsilon, n_epochs, batch_size, lr, c1, c2, device, env_name=""):
  # TODO...

다음은 논문의 PPO 교육 프로그램에 대한 의사 코드입니다.

PPO의 의사 코드는 비교적 간단합니다. 정책 모델의 여러 복사본(액터라고 함)을 통해 환경과의 상호 작용을 수집하고 이전에 정의된 목표를 사용하여 액터 및 비평가 네트워크를 최적화합니다.

실제로 얻은 누적 보상을 측정해야 하므로 버퍼가 주어질 때마다 보상을 누적 보상으로 대체하는 함수를 만들어야 합니다.

def compute_cumulative_rewards(buffer, gamma):
    """
    给定一个包含状态、策略操作逻辑、奖励和终止的缓冲区，计算每个时间的累积奖励并将它们代入缓冲区。
    """
    curr_rew = 0.

    # 反向遍历缓冲区
    for i in range(len(buffer) - 1, -1, -1):
        r, t = buffer[i][-2], buffer[i][-1]

        if t:
            curr_rew = 0
        else:
            curr_rew = r + gamma * curr_rew

        buffer[i][-2] = curr_rew

    # 在规范化之前获得平均奖励（用于日志记录和检查点）
    avg_rew = np.mean([buffer[i][-2] for i in range(len(buffer))])

    # 规范化累积奖励
    mean = np.mean([buffer[i][-2] for i in range(len(buffer))])
    std = np.std([buffer[i][-2] for i in range(len(buffer))]) + 1e-6
    for i in range(len(buffer)):
        buffer[i][-2] = (buffer[i][-2] - mean) / std

    return avg_rew

마지막에 누적 보상을 정규화합니다. 이것은 최적화 문제를 더 쉽게 만들고 훈련을 더 매끄럽게 만드는 표준 트릭입니다.

상태, 취한 행동, 행동 확률 및 누적 보상을 포함하는 버퍼가 있으므로 주어진 버퍼에서 최종 목표에 대한 세 가지 손실 조건을 계산하는 함수를 작성할 수 있습니다.

def get_losses(model, batch, epsilon, annealing, device="cpu"):
    """给定模型、给定批次和附加参数返回三个损失项"""
    # 获取旧数据
    n = len(batch)
    states = torch.cat([batch[i][0] for i in range(n)])
    actions = torch.cat([batch[i][1] for i in range(n)]).view(n, 1)
    logits = torch.cat([batch[i][2] for i in range(n)])
    values = torch.cat([batch[i][3] for i in range(n)])
    cumulative_rewards = torch.tensor([batch[i][-2] for i in range(n)]).view(-1, 1).float().to(device)

    # 使用新模型计算预测
    _, new_logits, new_values = model(states)

    # 状态动作函数损失(L_CLIP)
    advantages = cumulative_rewards - values
    margin = epsilon * annealing
    ratios = new_logits.gather(1, actions) / logits.gather(1, actions)

    l_clip = torch.mean(
        torch.min(
            torch.cat(
                (ratios * advantages,
                 torch.clip(ratios, 1 - margin, 1 + margin) * advantages),
                dim=1),
            dim=1
        ).values
    )

    # 价值函数损失(L_VF)
    l_vf = torch.mean((cumulative_rewards - new_values) ** 2)

    # 熵奖励
    entropy_bonus = torch.mean(torch.sum(-new_logits * (torch.log(new_logits + 1e-5)), dim=1))

    return l_clip, l_vf, entropy_bonus

실제로 우리는 1에서 시작하여 훈련 내내 선형적으로 0으로 감소하는 어닐링 매개변수를 사용합니다. 교육이 진행됨에 따라 정책이 점점 더 적게 변경되기를 원하기 때문입니다. 또한 및 new_logits와 변수의 기울기를 new_values추적하지 않고 텐서 차이만 추적합니다.advantages

이제 환경과 상호 작용하고 버퍼를 저장하고 (진정한) 누적 보상을 계산하고 손실 기간을 얻는 방법이 있으므로 최종 교육 코드 작성을 시작할 수 있습니다.

def training_loop(env, model, max_iterations, n_actors, horizon, gamma, epsilon, n_epochs, batch_size, lr,
                  c1, c2, device, env_name=""):
    """使用最多n个时间戳的多个actor在给定环境中训练模型。"""

    # 开始运行新的权重和偏差
    wandb.init(project="Papers Re-implementations",
               entity="peutlefaire",
               name=f"PPO - {
      
      env_name}",
               config={
    
    
                   "env": str(env),
                   "number of actors": n_actors,
                   "horizon": horizon,
                   "gamma": gamma,
                   "epsilon": epsilon,
                   "epochs": n_epochs,
                   "batch size": batch_size,
                   "learning rate": lr,
                   "c1": c1,
                   "c2": c2
               })

    # 训练变量
    max_reward = float("-inf")
    optimizer = Adam(model.parameters(), lr=lr, maximize=True)
    scheduler = LinearLR(optimizer, 1, 0, max_iterations * n_epochs)
    anneals = np.linspace(1, 0, max_iterations)

    # 训练循环
    for iteration in range(max_iterations):
        buffer = []
        annealing = anneals[iteration]

        # 使用当前策略收集所有actor的时间戳
        for actor in range(1, n_actors + 1):
            buffer.extend(run_timestamps(env, model, horizon, False, device))

        # 计算累积奖励并刷新缓冲区
        avg_rew = compute_cumulative_rewards(buffer, gamma)
        np.random.shuffle(buffer)

        # 运行几轮优化
        for epoch in range(n_epochs):
            for batch_idx in range(len(buffer) // batch_size):
                start = batch_size * batch_idx
                end = start + batch_size if start + batch_size < len(buffer) else -1
                batch = buffer[start:end]

                # 归零优化器梯度
                optimizer.zero_grad()

                # 获取损失
                l_clip, l_vf, entropy_bonus = get_losses(model, batch, epsilon, annealing, device)

                # 计算总损失并反向传播
                loss = l_clip - c1 * l_vf + c2 * entropy_bonus
                loss.backward()

                # 优化
                optimizer.step()
            scheduler.step()

        # 记录输出
        curr_loss = loss.item()
        log = f"Iteration {
      
      iteration + 1} / {
      
      max_iterations}: " \
              f"Average Reward: {
      
      avg_rew:.2f}\t" \
              f"Loss: {
      
      curr_loss:.3f} " \
              f"(L_CLIP: {
      
      l_clip.item():.1f} | L_VF: {
      
      l_vf.item():.1f} | L_bonus: {
      
      entropy_bonus.item():.1f})"
        if avg_rew > max_reward:
            torch.save(model.state_dict(), MODEL_PATH)
            max_reward = avg_rew
            log += " --> Stored model with highest average reward"
        print(log)

        # 将信息记录到 W&B
        wandb.log({
    
    
            "loss (total)": curr_loss,
            "loss (clip)": l_clip.item(),
            "loss (vf)": l_vf.item(),
            "loss (entropy bonus)": entropy_bonus.item(),
            "average reward": avg_rew
        })

    # 完成 W&B 会话
    wandb.finish()

마지막으로 모델이 최종적으로 어떻게 보이는지 확인하기 위해 다음 testing_loop기능을 .

def testing_loop(env, model, n_episodes, device):
    for _ in range(n_episodes):
        run_timestamps(env, model, timestamps=128, render=True, device=device)

이런 식으로 우리의 메인 프로그램은 매우 간단해질 것입니다.

def main():
    # 解析参数
    args = parse_args()
    print(args)

    # 设置种子
    pl.seed_everything(args["seed"])

    # 获取设备
    device = get_device()

    # 创建环境
    env_name = "CartPole-v1"
    env = gym.make(env_name)

    # 创建模型(actor和critic)
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)

    # 训练
    training_loop(env, model, args["max_iterations"], args["n_actors"], args["horizon"], args["gamma"], args["epsilon"],
                  args["n_epochs"], args["batch_size"], args["lr"], args["c1"], args["c2"], device, env_name)

    # 加载最佳模型
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
    model.load_state_dict(torch.load(MODEL_PATH, map_location=device))

    # 测试
    env = gym.make(env_name, render_mode="human")
    testing_loop(env, model, args["n_test_episodes"], device)
    env.close()

위의 내용이 전부입니다! 위의 코드를 이해했다면 축하합니다. PPO 알고리즘을 이해한 것입니다.

결론적으로

근접 정책 최적화는 거의 모든 설정에서 사용할 수 있는 정책 강화 학습을 위한 최신 최적화 알고리즘입니다. 또한 근접 정책 최적화는 상대적으로 간단한 목적 함수와 상대적으로 조정해야 할 하이퍼파라미터가 적습니다.

ChatGPT는 PPO에 의존하여 세 번째 단계에서 예상보다 많은 결과를 얻습니다. 자신의 강화 학습 작업에 사용할 수 있으며 예상치 못한 결과를 얻을 수 있습니다.