PhyCRNet을 기반으로 시공간 PDE를 해결합니다.

오픈소스 중국 커뮤니티 팀이 공유라는 이름으로 오픈소스 중국 커뮤니티의 뒷이야기를 전하는 첫 생방송을 진행했습니다."

저자: 유 팬

배경

편미분 방정식으로 모델링된 복잡한 시공간 시스템은 응용 수학, 물리학, 생물학, 화학, 공학 등 다양한 분야에서 널리 사용됩니다. 대부분의 경우 이러한 복잡한 물리적 시스템을 설명하는 데 사용되는 PDE에 대한 분석 솔루션을 얻을 수 없으므로 유한 요소, 유한 차이, 등하학 분석(IGA) 및 기타 방법을 포함한 수치 솔루션 방법이 광범위하게 연구되었습니다. 이러한 전통적인 수치 방법은 기저 함수를 통해 방정식의 정확한 해를 근사화할 수 있지만 데이터 동화 및 역 문제 해결에는 여전히 엄청난 계산 오버헤드가 있습니다.

최근에는 비선형 시스템의 순방향 및 역방향 문제를 해결하기 위해 다양한 딥러닝 방법이 끊임없이 등장하고 있습니다. DNN을 사용하여 물리적 시스템을 모델링하는 연구는 크게 연속 네트워크와 이산 네트워크의 두 가지 범주로 나눌 수 있습니다. 연속 네트워크의 대표적인 대표는 PINN입니다. PDE의 잔차는 신경망의 소프트 제약 조건으로 사용되며 완전 연결 레이어는 방정식의 해를 근사화하는 데 사용되며 모델은 작은 데이터 규모 또는 라벨이 지정되지 않은 샘플링 데이터도 마찬가지입니다. 그럼에도 불구하고 PINN은 저차원 매개변수화로 제한되는 경우가 많으며 가파른 경사와 복잡한 로컬 형태가 있는 PDE 시스템에 직면할 때 확장됩니다. 최근 소수의 파일럿 연구에서는 개별 네트워크가 연속 학습보다 더 나은 확장성과 더 빠른 수렴 속도를 갖는 것으로 나타났습니다. 예를 들어 CNN은 물리적 및 참조를 사용하는 시간 독립적인 시스템의 직사각형 영역에서 프록시 모델로 사용될 수 있습니다. 시간 종속 시스템의 경우 좌표 변환을 통해 정상 상태 편미분 방정식을 기하학적으로 적응적으로 풀기 위해 대부분의 신경망 솔루션 방법은 여전히 데이터 기반 및 메싱을 기반으로 합니다.

중국 런민 대학교 힐하우스 인공 지능 학교 Sun Hao 교수 팀이 미국 노스이스턴 대학교 및 노트르담 대학교와 협력하여 제안한 PhyCRNet[1]은 다차원 시공간 영역에서 PDE를 해결하기 위한 비지도 방법입니다. ConvLSTM(저차원 공간 특징 추출 및 학습 시간 진화), 전역 잔차 연결(시간 축에서 방정식 해의 변화를 엄격하게 매핑) 및 고차 유한 차분을 결합한 학습 방법입니다. 시공간 필터링(잔차 손실 함수 구성 결정 필수 PDE 파생 기능)은 역 문제에 직면하고 희소하고 잡음이 많은 데이터가 있는 경우 기본 솔루션이 됩니다.

1. 문제 정의

다차원 비선형 모수 편미분 방정식을 고려하면 일반적인 형태는 다음과 같습니다.

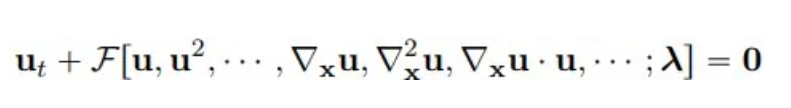
여기서 u(x, t)는 시간 영역 T와 공간 영역 Ω에서 방정식의 해를 나타내고, F는 매개변수 λ를 갖는 비선형 함수입니다.

**2.** 모델 방법

ConvLSTM

ConvLSTM은 LSTM 및 변형 LSTM 인코더-디코더 예측 아키텍처(시간이 지남에 따라 진화하는 장기 종속성을 모델링하는 이점이 있음)에서 확장되는 시공간 시퀀스 간 학습 프레임워크입니다. 본질적으로 메모리 장치는 입력 및 상태 정보에 액세스하여 업데이트되고, 메모리의 축적 및 삭제는 교묘하게 설계된 제어 게이트를 통해 완료됩니다. 이 설정을 기반으로 일반 순환 신경망(RNN)의 기울기 소멸 문제가 완화됩니다. ConvLSTM은 LSTM의 기본 구조(예: 셀 단위 및 게이트)를 상속하여 정보 흐름을 제어하고, CNN이 더 나은 공간 연결 표현 기능을 가지고 있다는 점을 고려하여 완전 연결 신경망(FC-NN)을 수정하고 CNN에서 게이팅 작업을 수행합니다. . RNN의 특별한 유형인 LSTM은 시간 종속 PDE 방정식을 풀기 위한 암시적 수치 방법으로 사용될 수 있습니다. 단일 ConvLSTM 유닛의 구조 다이어그램은 다음과 같습니다.

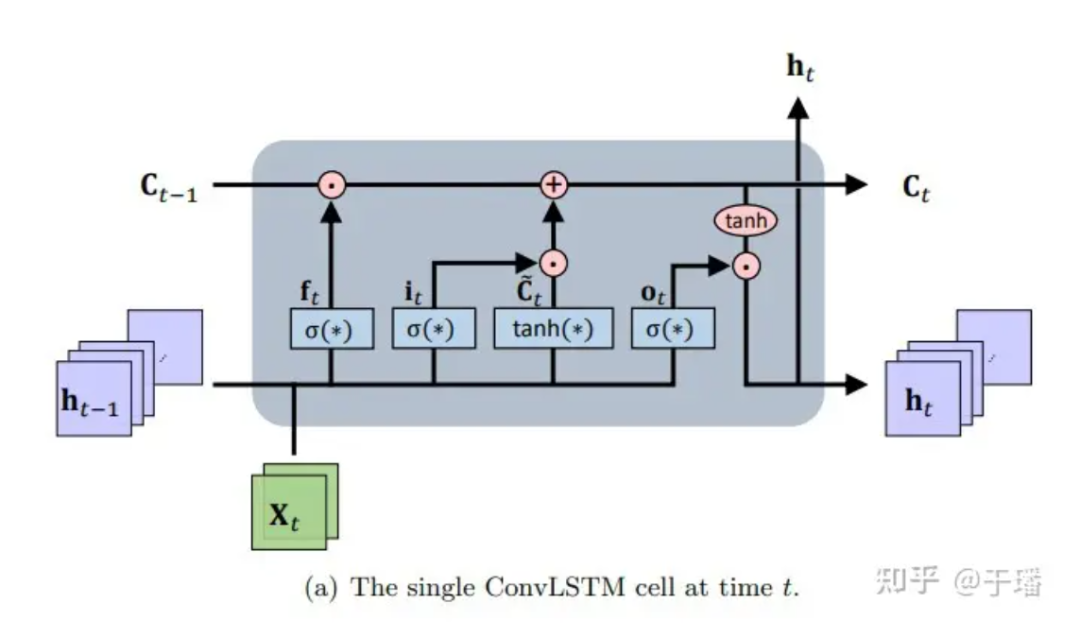그림 1: 시간 t에서의 단일 ConvLSTM 셀

ConvLSTM 단위 업데이트의 수학적 표현은 다음과 같습니다.

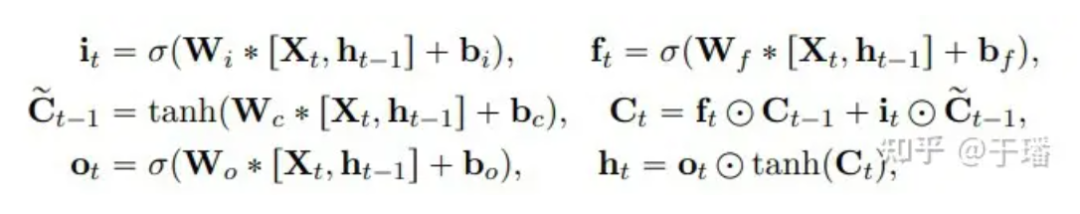
그 중 *는 컨벌루션 연산을 나타내고, ⊙는 Hadamard 곱을 나타내며, W는 필터의 가중치 매개변수, b는 바이어스 벡터를 나타냅니다.

픽셀 셔플

픽셀 셔플은 저해상도(LR) 이미지를 고해상도(HR) 이미지로 업샘플링하는 효율적인 하위 픽셀 컨볼루션 작업입니다. LR 피처 텐서의 차원이 (C 차원 (C, H xr, W xr)을 갖는 HR 텐서라고 가정합니다. 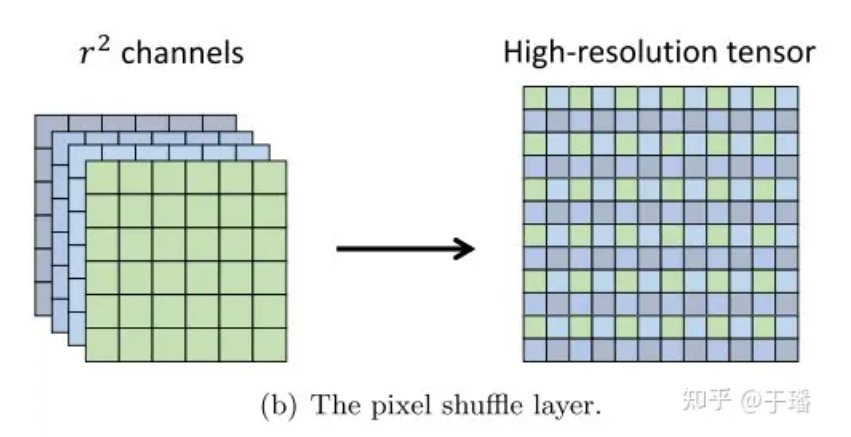그림 2: 픽셀 셔플 레이어

Pixel Shuffle의 효율성은 다음에 반영됩니다. (1) 컨볼루션의 마지막 레이어에서만 해상도를 높이면 디컨볼루션과 같은 목표 해상도로 이미지를 높이기 위해 더 많은 컨볼루션 레이어를 사용할 필요가 없습니다. 업샘플링 레이어 이전의 모든 특징 추출 레이어에서는 이러한 저해상도 텐서를 처리하는 데 더 작은 필터를 사용할 수 있습니다.

PhyCRNet

PhyCRNet은 인코더-디코더 모듈, 잔여 연결, 자동 회귀 프로세스 및 필터 기반 차동 방법으로 구성됩니다. 인코더에는 특정 순간의 상태 변수 Ui로부터 저차원 잠재 특성을 학습하고 ConvLSTM을 통해 시간이 지남에 따라 진화할 수 있도록 3개의 컨볼루셔널 레이어가 포함되어 있습니다. 저차원 변수에 대해 변환이 수행되므로 그에 따라 메모리 오버헤드가 줄어듭니다. 또한 순방향 오일러 방법에서 영감을 받아 입력 변수 Ui와 출력 변수 Ui+1 사이에 전역 잔차 연결을 추가할 수 있으며 단일 단계 학습 과정은 Ui+1 = Ui + δt x N으로 표현할 수 있습니다. [Ui; θ], 여기서 N[·]은 훈련된 신경망 연산자를 나타내고 δt는 단위 시간 간격입니다. 따라서 이 재귀 관계는 단순한 자기회귀 과정으로 볼 수 있습니다.

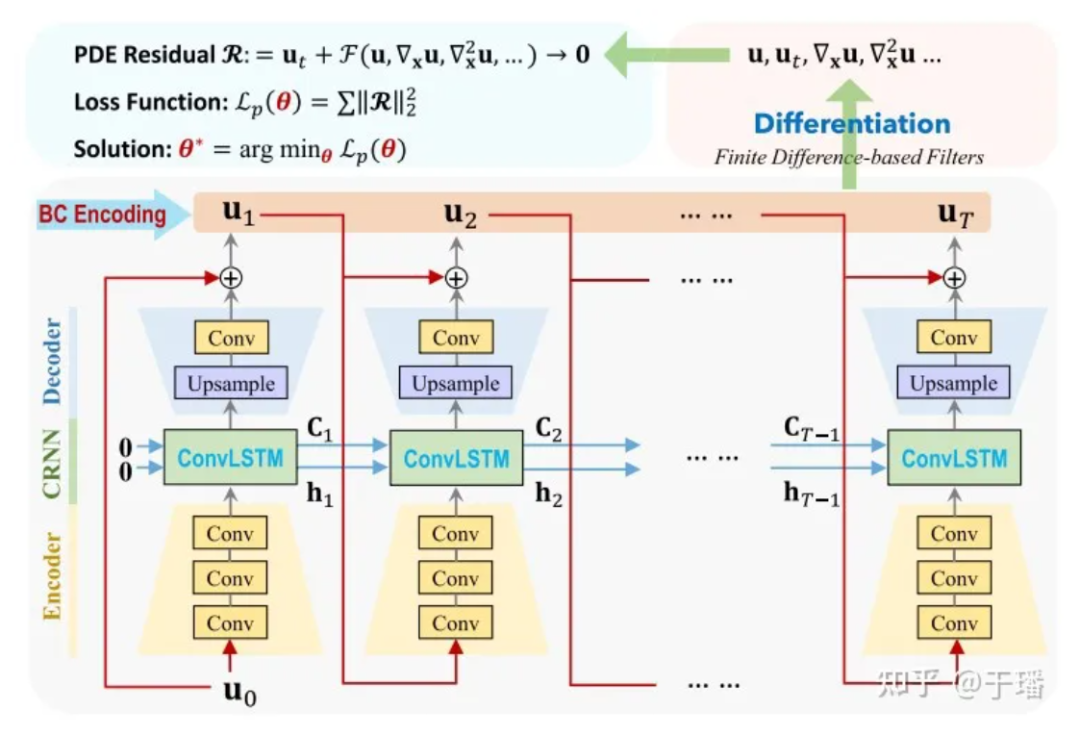그림 3: PhyCRNet 네트워크 구조 다이어그램

여기서 U0은 초기 조건이고, U1에서 UT까지는 모델에서 예측해야 하는 이산 솔루션이며, 입력에서 출력까지의 시간 변화는 기존 수치 방법과 비교하여 ConvLSTM은 더 큰 시간 간격을 사용할 수 있습니다. 각 미분 항의 계산을 위해 고정 컨볼루션 커널[1]을 사용하여 차이 값을 나타냅니다. PhyCRNet에서는 2차 및 4차 차이 항을 사용하여 시간과 공간에 대한 U의 도함수를 계산합니다. 컴퓨팅 성능을 더욱 최적화하기 위해 각 주기의 첫 번째 순간을 제외하고 크기 T 주기에서 인코더 부분을 건너뛸 수 있습니다. 회로도는 다음과 같습니다.

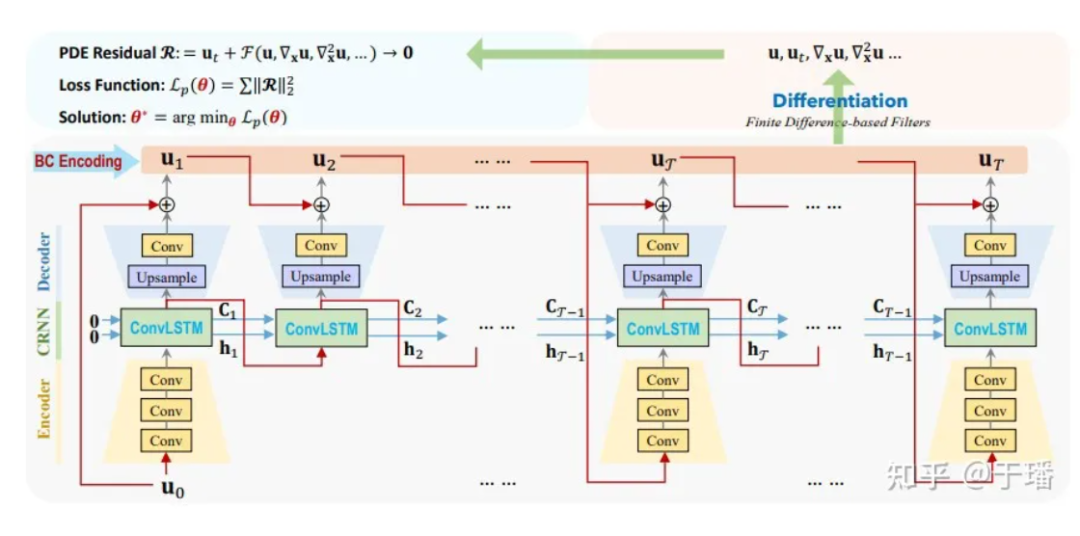그림 4: PhyCRNet-s 네트워크 구조 다이어그램

I/BC 하드 제약 조건

물리적 초기 경계 조건을 소프트 제약 조건(잔차는 손실의 일부로 최적화됨)으로 사용하는 PINN 방법과 비교하여 PhyCRNet은 I/BC를 모델에 하드 코딩하는 방법을 사용합니다(초기 조건은 입력 U0으로 사용됨) ConvLSTM의 경계 조건은 패딩을 통해 인코딩됨), 물리적 조건이 더 이상 소프트 제약 조건이 아니므로 모델의 정확도와 수렴 속도가 향상됩니다. Dirichlet BC의 경우 알려진 상수 경계 값이 공간 영역에서 패딩으로 직접 채워질 수 있는 반면, Neumann BC의 경우 공간 영역(고스트 요소) 주위에 고스트 요소 레이어가 추가될 수 있습니다. 훈련 과정 중 차이를 통해 대략적으로 계산됩니다.

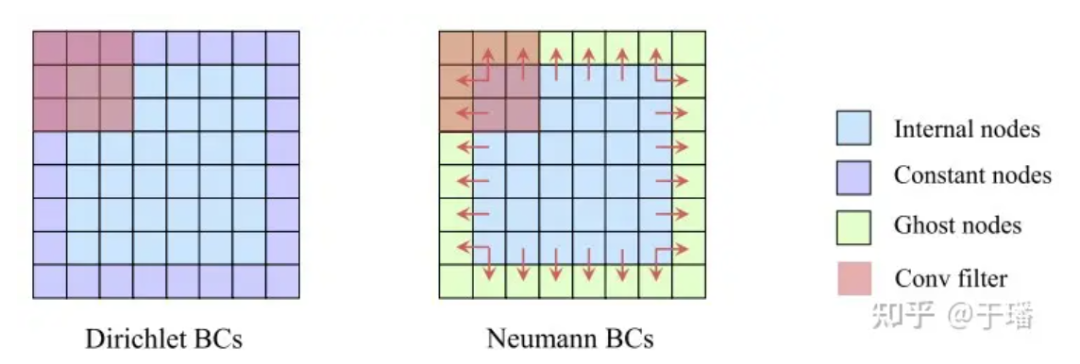그림 5: 경계 조건에 대한 엄격한 제약 조건 예시

손실 함수

I/BC는 모델에서 엄격하게 제한되어 있으므로 손실 함수에는 PDE의 잔차 항만 포함하면 됩니다. 2차원 PDE 시스템을 예로 들면 손실 함수는 다음과 같이 표현될 수 있습니다.

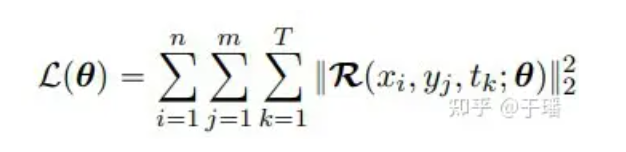
여기서 n과 m은 그리드의 높이와 너비를 나타내고, T는 총 시간 단계 수이며, R(x, t; θ)는 PDE의 잔차입니다.

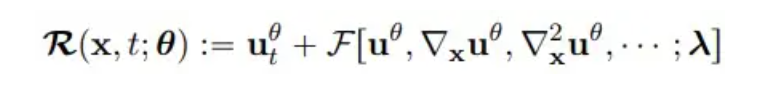
**3. ** 결과 분석

전체 영역에서 모델 오류를 평가하기 위해 시간 τ에서의 누적 평균 제곱근 오류(a-RMSE)는 다음과 같이 계산됩니다.

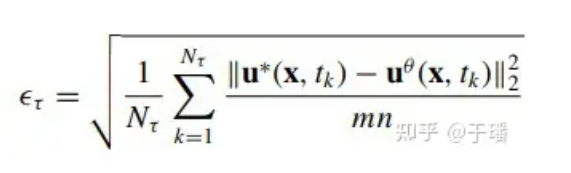
여기서 Nτ는 [0, τ]의 시간 단계 수이고 u*(x, t)는 방정식의 기준 솔루션입니다.

2차원 버거 방정식

다음 형식의 2차원 버거 방정식이 주어지면 유체 역학의 고전적인 문제를 고려하십시오.

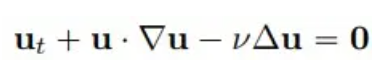
PhyCRNet 및 PINN 방법의 솔루션 정확도와 외삽 기능을 비교하기 위해 교육(t = 1.0, 2.0) 및 외삽(t = 3.0, 4.0)의 4개 시점을 선택합니다.

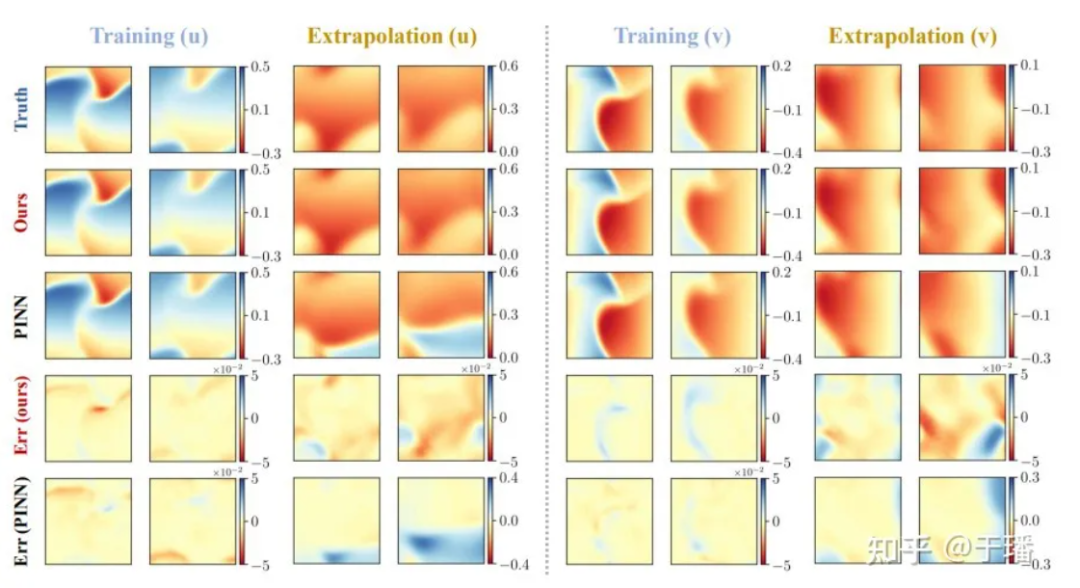그림 6: 2차원 버거 방정식에 대한 PhyCRNet 대 PINN의 훈련 및 외삽 결과

λ-Ω RD 방정식

두 번째 경우로, 2차원 λ-Ω RD 시스템(종종 다중 규모 생화학적 과정을 나타내는 데 사용됨)을 고려하십시오.

그 중 u와 v는 다음을 만족하는 두 개의 필드 변수입니다.

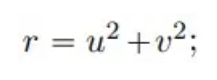
λ 및 Ω는 두 가지 실수 값 함수입니다.

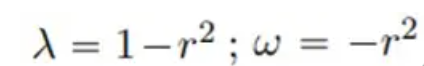
[-10, 10] 영역의 총 801개 시간 단계에 대한 참조 솔루션은 스펙트럼 방법으로 생성되며, [0, 5] 시간 간격에서 200개 시간 단계에 대한 학습 후 [5, 10]에 대한 참조 솔루션이 생성됩니다. ] 해당 기간 동안 예측이 이루어지며, PhyCRNet과 PINN을 비교한 예측 결과는 다음과 같습니다.

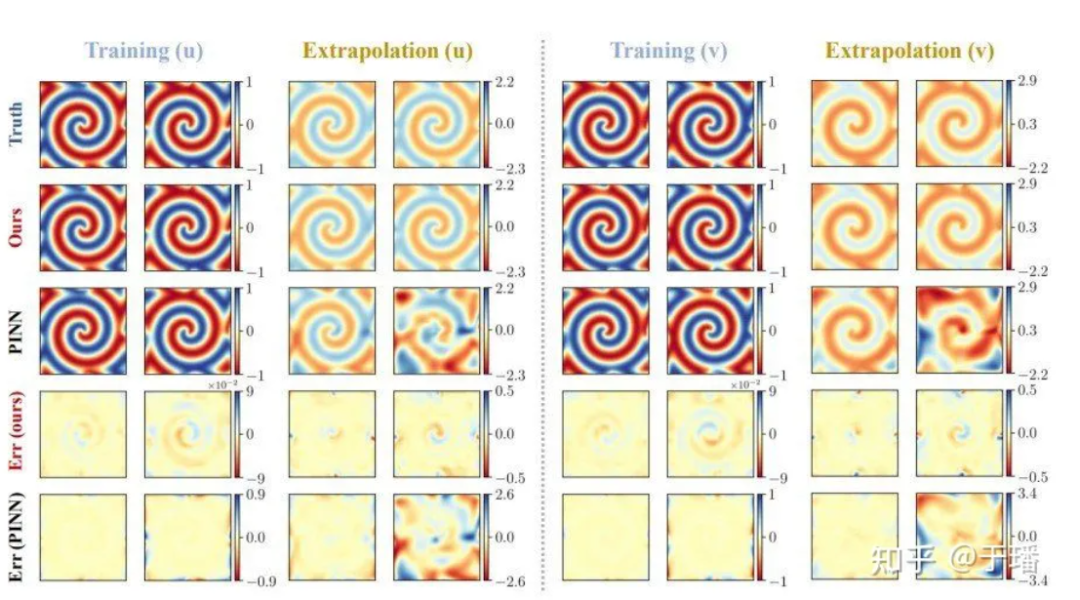그림 7: PhyCRNet 대 PINN 훈련 및 λ-Ω RD 방정식에 대한 외삽 결과

아래 그림은 위에서 언급한 두 PDE 시스템의 훈련 및 외삽 동안 PhyCRNet과 PINN의 오류 전파 곡선을 보여줍니다. PhyCRNet이 두 단계(특히 외삽 단계)에서 더 나은 성능을 발휘한다는 것을 분명히 볼 수 있습니다.

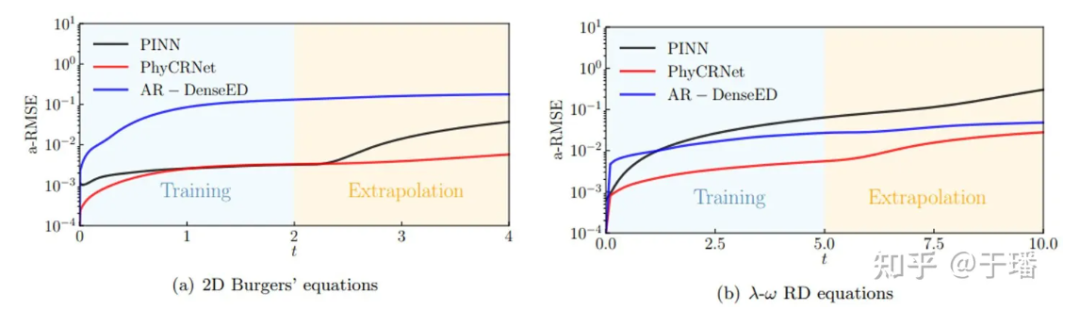그림 8: PhyCRNet과 PINN의 오류 전파 비교

참고자료

[1] Ren P, Rao C, Liu Y, 외. PhyCRNet: 시공간 PDE를 해결하기 위한 물리학 정보 컨볼루션-반복 네트워크[J]. 응용 기계 및 공학의 컴퓨터 방법, 2022, 389: 114399.

[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub

PhyCRNet을 기반으로 시공간 PDE를 해결합니다.

참고자료

추천