저자: 유 팬
배경
인공지능(AI)의 발전은 과학적 발견에 새로운 패러다임을 제시했습니다. 오늘날 AI는 광범위한 공간적, 시간적 규모에 걸쳐 자연 현상에 대한 이해를 향상시키고 가속화하며 가능하게 하여 자연과학의 발전을 촉진하고 AI4Science라는 새로운 연구 분야를 탄생시켰습니다. 최근 60명 이상의 저자가 공동으로 작성한 리뷰 논문 "양자, 원자 및 연속체 시스템의 과학을 위한 인공 지능"은 아원자, 원자 및 연속체 시스템의 하위 분야에 대한 심층적인 기술 요약을 제공합니다. 여기에서는 이 리뷰의 기술적 백본을 추출하고 대칭 변환 하에서 등변 모델을 구성하는 방법에 중점을 둡니다.
1. 소개
1929년 양자 물리학자 폴 디랙(Paul Dirac)은 다음과 같이 언급했습니다. "대부분의 물리학과 모든 화학의 수학적 이론에 필요한 기본 물리 법칙은 이미 우리에게 완전히 알려져 있으며, 이러한 법칙을 정확하게 적용하면 다음과 같은 문제가 발생한다는 사실에 어려움이 있습니다. complex 이는 양자물리학의 슈뢰딩거 방정식부터 유체역학의 나비에-스토크스 방정식까지 적용됩니다. 딥러닝은 이러한 방정식의 해결 속도를 높일 수 있습니다. 기존 시뮬레이션 방법의 결과를 교육 데이터로 사용하고 일단 교육을 받으면 이러한 모델은 기존 시뮬레이션보다 훨씬 빠르게 예측할 수 있습니다.
생물학과 같은 다른 분야에서는 근본적인 생물물리학적 과정이 완전히 이해되지 않을 수 있으며 궁극적으로 수학 방정식으로 설명되지 않을 수도 있습니다. 이러한 경우, 실험을 통해 얻은 단백질 예측 모델 AlphaFold, RoseTTAFold, ESMFold 및 기타 3D 구조와 같이 실험적으로 생성된 데이터를 사용하여 딥러닝 모델을 훈련할 수 있으므로 계산적으로 예측된 단백질 3D 구조의 정확도가 실험 결과와 유사할 수 있습니다. .
1.1 과학 분야
이 기사에서 관심 있는 과학 분야는 모델링되는 물리적 시스템의 공간적 및 시간적 규모에 따라 아래 그림의 개요로 구성됩니다.
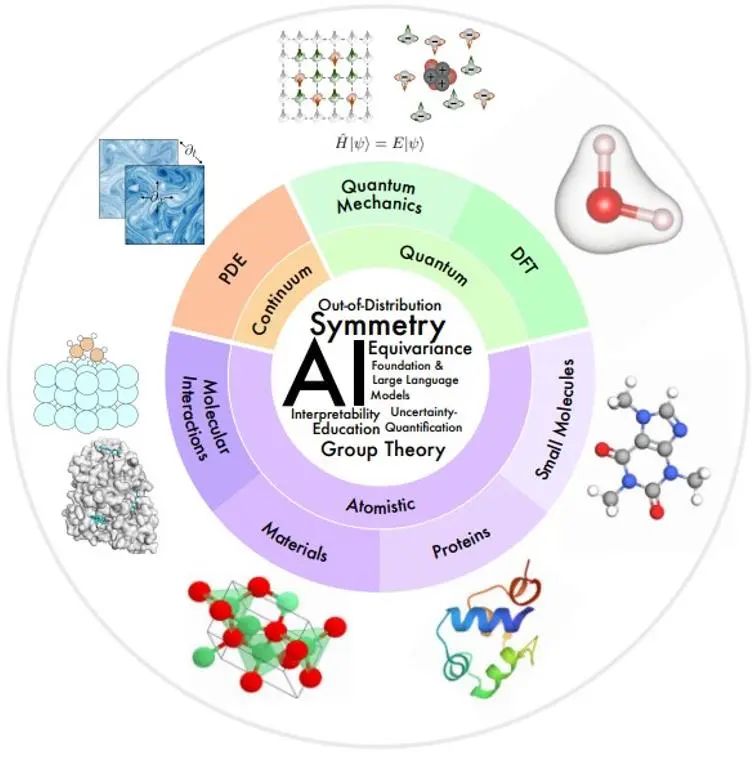
소규모: 양자 역학은 파동 함수를 사용하여 가장 작은 규모에서 물리적 현상을 연구합니다. 슈뢰딩거 방정식은 양자 시스템의 완전한 동적 과정을 설명하지만 기하급수적인 복잡성을 가져옵니다. 밀도 범함수 이론 (DFT)과 순순한 양자화학 방법은 분자와 물질의 전자 구조와 물리적 특성을 계산하기 위해 실제로 널리 사용되는 제1원리 방법이며, 분자와 고체의 전자적, 기계적 특성을 더 추론할 수 있습니다. , 자기 및 촉매 특성. 그러나 이러한 방법은 여전히 계산 비용이 많이 들고 소규모 시스템(~1000개 원자)으로 사용이 제한됩니다. AI 모델은 속도와 정확성을 향상시키는 데 도움이 될 수 있습니다.
중규모(Mesoscale): 일반적으로 크기가 수십에서 수백 개의 원자인 작은 분자는 많은 화학적 및 생물학적 과정에서 중요한 조절 및 신호 전달 역할을 합니다. 단백질은 하나 이상의 아미노산 사슬로 구성된 큰 분자입니다. 아미노산 서열은 단백질 구조를 결정하고, 이는 다시 단백질의 기능을 결정합니다. 재료 과학 연구는 가공, 구조, 특성 및 재료 간의 관계를 연구합니다 . 분자 상호작용은 리간드-수용체 상호작용, 분자-물질 상호작용 등 분자 상호작용을 통해 얼마나 많은 물리적, 생물학적 기능이 수행되는지 연구합니다. 이러한 분야에서 AI는 분자 특성화 및 생성, 분자 역학, 단백질 구조 예측 및 설계, 재료 특성 예측 및 구조 생성 분야에서 많은 진전을 이루었습니다.
대규모: 연속체 역학은 편미분 방정식을 사용하여 유체 흐름, 열 전달, 전자기파 등을 포함하여 거시적 수준에서 시간과 공간에 따라 진화하는 물리적 프로세스를 모델링합니다. AI 방법은 계산 효율성 향상, 일반화 및 다중 해상도 분석과 같은 문제에 대한 몇 가지 솔루션을 제공합니다.
1.2 AI 기술 분야
과학적 AI의 여러 영역에 걸쳐 공통된 기술적 과제가 존재합니다.
**대칭:**대칭은 매우 강력한 유도 편집증이므로 AI4Science의 주요 과제는 AI 모델에 대칭을 효과적으로 통합하는 방법입니다.
**해석 가능성:**AI4Science에서 해석 가능성은 물리적 세계의 법칙을 이해하는 데 매우 중요합니다.
**배포 외(OOD) 일반화 및 인과성: **각각의 다양한 설정에 대한 훈련 데이터 생성을 방지하려면 OOD 일반화를 가능하게 하는 인과 요인을 식별해야 합니다.
**기본 모델 및 대규모 언어 모델:**자연어 처리 작업의 기본 모델은 자가 감독 또는 일반화 가능한 감독 하에 사전 학습되어 퓨샷 또는 제로샷 방식으로 다양한 다운스트림 작업을 수행합니다. 이 기사는 이 패러다임이 AI4Science 발견을 어떻게 가속화할 수 있는지에 대한 관점을 제공합니다.
**불확도 정량화(UQ): **데이터 및 모델 불확실성 하에서 강력한 의사 결정을 보장하는 방법을 연구합니다.
**교육:** 학습과 교육을 촉진하기 위해 이 기사에서는 저자가 유용하다고 생각하는 분류된 리소스 목록을 제공하고 커뮤니티가 AI와 과학 및 교육의 통합을 더 잘 촉진할 수 있는 방법에 대한 관점을 제공합니다.
**2. ** 대칭, 등분산 및 그 이론
많은 과학적 문제에서 관심 개체는 일반적으로 3D 공간에 위치하며 개체의 수학적 표현은 참조 좌표계에 의존하므로 이러한 표현은 좌표계를 기준으로 합니다. 그러나 좌표계는 본질적으로 존재하지 않으므로 좌표계와 독립적인 표현이 필요합니다. 따라서 AI4Science의 주요 과제 중 하나는 좌표계 변환에서 불변성 또는 등분성을 달성하는 방법입니다.
2.1 개요
대칭이란 좌표 변환과 같은 특정 변환 하에서 물리적 현상의 특성이 변경되지 않고 유지된다는 사실을 나타냅니다. 시스템에 특정 대칭이 존재하는 경우 예측 대상은 해당 대칭 변환에 따라 자연스럽게 불변 또는 등변입니다. 예를 들어 3차원 분자의 에너지를 예측할 때 3차원 분자가 이동하거나 회전해도 예측값은 변하지 않습니다. 대칭 인식 학습을 달성하기 위한 대체 전략은 지도 학습에서 데이터 증대를 사용하는 것입니다. 특히 입력 데이터와 레이블에 무작위 대칭 변환을 적용하여 모델이 대략적인 등변적 예측을 출력하도록 하는 것입니다. 그러나 여기에는 많은 단점이 있습니다.
1) 좌표계 선택 시 추가적인 자유도를 고려하면 모델은 원래 고정된 좌표계에서 단순한 패턴을 표현하기 위해 더 큰 용량이 필요합니다.
2) 변환과 같은 많은 대칭 변환은 무한한 수의 등변 샘플을 생성할 수 있으므로 제한된 데이터 향상이 데이터의 대칭을 완전히 반영하기 어렵게 만듭니다.
3) 어떤 경우에는 좋은 예측 결과를 얻기 위해 매우 심층적인 모델을 구축해야 합니다. 모델의 각 계층이 등분산을 유지할 수 없으면 전체 등분산 출력을 예측하기가 어렵습니다.
4) 분자 모델링과 같은 과학적인 문제에서는 머신러닝이 신뢰할 수 있게 사용될 수 있도록 대칭 변환에 강인한 예측을 제공하는 것이 중요합니다.
데이터 증대의 많은 단점으로 인해 대칭 요구 사항을 충족하는 기계 학습 모델을 설계하는 데 점점 더 많은 연구가 집중되고 있습니다. 대칭 적응 아키텍처에서 모델은 데이터 강화 없이 학습 목표 예측 작업에 집중할 수 있습니다.
2.2 이산 대칭 변환에서의 등가성
이 섹션에서 저자는 AI 모델의 이산 대칭 변환에서 등분산을 유지하는 예를 제공합니다. 이 예제 문제는 한 순간에서 다음 순간까지 2D 평면에서 스칼라 흐름장의 매핑을 시뮬레이션합니다. 입력 유동장이 90도, 180도, 270도 회전하면 출력 유동장도 그에 따라 회전합니다. 수학적 표현은 다음과 같습니다.
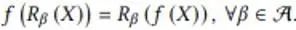
여기서 f는 흐름장 매핑 함수를 나타내고 R은 이산 회전 변환을 나타냅니다. Cohen et al.은 이 문제를 해결하기 위해 등변 그룹 컨볼루션 신경망(G-CNN)을 제안했습니다. 가장 간단한 기본 구성 요소는 오름차순 컨볼루션입니다.
1) 먼저 대칭 변환에서 컨볼루션 커널을 모든 각도로 회전시키고 회전된 컨볼루션 커널을 사용하여 입력에 대해 해당 컨볼루션 작업을 수행하여 여러 기능 레이어를 얻은 다음 새로 생성된 회전 차원 α에 이러한 기능 레이어를 함께 쌓습니다. ) 이 회전 차원 α에서 풀링이 수행되므로 입력 X가 회전할 때 결과 출력이 해당 회전을 생성합니다.
풀링 작업이 있기 때문에 등변 행이 유지되지만 이러한 기능은 방향 정보를 전달할 수 없습니다. 일반적으로 G-CNN은 다음 그림과 같은 구조를 채택합니다.
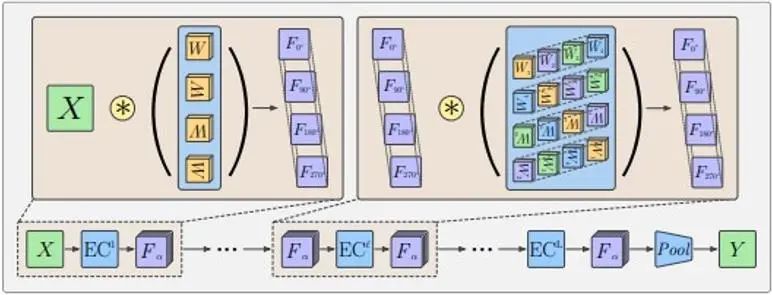
먼저 회전 컨볼루션 커널을 사용하여 입력의 차원을 늘린 다음 다층 그룹 컨볼루션 계층을 사용하여 각 기능 계층이 회전 차원을 유지하면서 회전 등분산 요구 사항을 충족하도록 하고 마지막으로 풀링 계층을 사용합니다. 회전 치수를 제거하는 데 사용됩니다. 이를 통해 중간 피처 레이어는 피처의 상대적 위치와 방향에서 패턴을 더 잘 감지할 수 있습니다. 중간 특징 레이어의 등분산의 의미는 회전 변환에 따라 특징 레이어가 회전하고 회전 차원의 순서도 회전하며 사용된 그룹 콘볼루션 레이어의 콘볼루션 커널의 회전 및 회전 설계도 만든다는 것입니다. 출력 피처 레이어는 이러한 등분산 특성을 유지할 수 있습니다.
2.3-2.5 3차원 연속변환의 등변모델 구축
많은 과학적 문제에서 우리는 3D 공간에서의 연속 회전 및 병진 대칭에 중점을 둡니다. 예를 들어, 화학 분자의 구조가 회전하고 병진할 때 예측된 분자 속성으로 구성된 벡터는 해당 변환을 겪게 됩니다. 이러한 연속 회전 변환 R과 변환 변환 t는 SE(3) 그룹의 요소를 구성하며 이러한 변환은 벡터 공간에서 변환 행렬로 표현될 수 있습니다. 서로 다른 벡터 공간의 변환 행렬은 다를 수 있지만 이러한 벡터 공간은 독립적인 하위 벡터 공간으로 분해될 수 있습니다. 각 부분공간에는 동일한 변환 규칙이 있습니다. 즉, 그룹의 모든 변환 요소를 부분 공간의 벡터에 적용하여 얻은 벡터는 여전히 부분 공간에 있으므로 그룹의 변환 요소는 기약일 수 있습니다. 부분 공간 변환 행렬 표현. 예를 들어 SE(3) 그룹 요소의 작용에 따라 전체 에너지 및 에너지 갭과 같은 스칼라는 변경되지 않으며 해당 변환 행렬은 SE(3) 그룹 요소 아래에서 D^0(R)=1로 표현됩니다. 힘장과 같은 3D 벡터 해당 회전은 동작 하에서 발생하며, 그 변환 행렬은 고차원 벡터 공간에서 D^1(R)=R로 표현되며, D^l(R)은 2l+1입니다. -차원 정사각형 행렬. 이러한 변환 행렬 D^l(R)은 회전 R에 해당하는 l차 Wigner-D 행렬이라고 하며, 해당 하위 벡터 공간은 SE(3) 그룹의 l차 기약 불변 부분공간이 되며, 그 안의 벡터를 l Order Equivariant 벡터라고 합니다. 변환 변환에서 이러한 벡터는 항상 변경되지 않은 상태로 유지됩니다. 왜냐하면 우리가 관심을 갖는 속성은 상대적 위치에만 관련되기 때문입니다.
SE(3) 그룹의 불변 부분공간에 있는 특징에 3D 기하학적 정보를 매핑하는 일반적인 방법은 구면 조화 함수 매핑을 사용하는 것입니다. 구면 조화 함수 Y^l은 3차원 벡터를 2l+1차원 벡터로 매핑하며, 이는 입력 벡터가 2l+1 기본 구면 조화 함수로 분해될 때의 계수를 나타냅니다. 아래 그림과 같이 제한된 개수의 베이스만 사용하기 때문에 3차원 벡터로 표현되는 구에 대한 델타 함수는 어느 정도 넓어지게 됩니다.

구형 고조파에는 다음과 같은 등변 속성이 있습니다.
그 중 D는 앞서 언급한 l-order Wigner-D 행렬이다. 따라서 공간 함수는 회전 변환을 통해 서로 다른 차수의 등변 벡터의 조합으로 분해됩니다.
원자 좌표를 노드로 사용하는 그래프 신경망에서 노드 특징 h가 l_1 차의 등변 벡터라고 가정하면 다음 그래프 정보 전송 및 업데이트를 통해 업데이트된 h도 등분성을 유지하도록 할 수 있습니다.
여기서 핵심 단계는 정보 전송 중 텐서 곱 작업(TP)입니다. 그 중 vec는 행렬을 벡터화한다는 뜻이고, 계수 C는 2l_3+1행(2l_1+1)(2l_2+1)열의 행렬이다.
노드 특징 h는 l_1차의 기약 불변 부분공간의 벡터입니다. 에지 방향 r_ij의 구형 조화 함수 Y는 l_2차의 기약 불변 부분공간의 벡터입니다. 공간은 축소 가능하며 계수 C는 이 축소 가능한 공간에서 l_3차의 환원 불가능한 불변 부분 공간으로의 변환 관계입니다. 예를 들어, 두 개의 3차원 벡터의 직접 곱 공간은 다음과 같습니다.
직접 곱 공간의 회전 변환 행렬은 위 그림의 중앙에 있는 3블록 대각 행렬로 변환될 수 있는데, 이는 이 공간이 1, 3, 5 차원의 3개의 기약 불변 부분 공간으로 분해될 수 있음을 의미하며, 즉, 3⨂ 3=1⊕3⊕5의 벡터 공간을 분해합니다. 계수 C는 이 9차원 공간에서 각각 1차원, 3차원, 5차원 공간으로의 변환 행렬입니다. 위 공식에서 l_1, l_2, l_3은 모두 하나의 값만 가지며 고정 순서의 등변 특성입니다. 실제 네트워크의 특성은 이러한 서로 다른 순서 특성의 조합일 수 있습니다.
2.6-2.7 이전 예에서는 군론 이론과 구면 조화 함수의 특성이 사용되었습니다. 그룹 이론과 구면 조화 함수에 대한 기본 지식이 기사의 이 두 장에서 자세히 소개됩니다.
2.8 조정 가능한 커널은 등변 네트워크의 일반적인 형태를 구성합니다.
이산적이고 연속적인 변환을 적용한 이전의 등변 네트워크 계층은 통합 변수 컨볼루션(조정 가능한 CNN)의 형태로 설명할 수 있습니다.
그 중 x와 y는 공간 좌표이고, f_in(y)는 y 좌표의 입력 특징 벡터를 나타내고, f_out(x)는 x 좌표의 출력 특징 벡터를 나타내며, K는 입력 특징 공간에서 출력 특징으로의 변환입니다. 공간. 컨볼루션 작업은 병진 등분산을 보장합니다. 다른 공간 아핀 변환에서 등분산을 보장하려면 컨볼루션 커널 K도 다음 대칭 제약 조건을 충족해야 합니다.
그 중 g는 공간 변환 그룹에서의 변환이고, ρ_in과 ρ_out은 각각 입력 특징 공간과 출력 특징 공간(즉, 변환 행렬)에서의 변환 표현을 나타낸다.
이 시점에서 대칭과 등분산에 대한 기사의 이론적 설명은 기본적으로 끝났고, 이어서 1장에 나열된 여러 분야에 대한 별도의 개요가 이어졌습니다.
참고자료
[1] Ren P, Rao C, Liu Y, 외. PhyCRNet: 시공간 PDE를 해결하기 위한 물리학 정보 컨볼루션-반복 네트워크[J]. 응용 기계 및 공학의 컴퓨터 방법, 2022, 389: 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
【1】 Xuan Zhang, Limei Wang, Jacob Helwig 등 2023. 양자, 원자 및 연속체 시스템의 과학을 위한 인공 지능. arXiv: https://arxiv.org/abs/2307.08423
【2】 타코 코헨과 맥스 웰링. 2016. 그룹 등변 컨벌루션 네트워크. 머신러닝에 관한 국제 컨퍼런스에서. PMLR, 48:2990-2999.
【3】 Nathaniel Thomas, Tess Smidt, Steven Kearnes 등 2018. 텐서 필드 네트워크: 3D 포인트 클라우드를 위한 회전 및 평행 이동 등변 신경망. arXiv: https://arxiv.org/abs/1802.08219
모리스 와일러(Maurice Weiler), 마리오 가이거(Mario Geiger), 맥스 웰링(Max Welling) 등 2018. 3D 조정 가능한 CNN: 체적 데이터에서 회전 등변적 특징 학습. 신경 정보 처리 시스템의 발전
1990년대에 태어난 프로그래머가 비디오 포팅 소프트웨어를 개발하여 1년도 안 되어 700만 개 이상의 수익을 올렸습니다. 결말은 매우 처참했습니다! Google은 Flutter, Dart 및 Python 팀의 중국 코더의 "35세 저주"와 관련된 정리해고를 확인했습니다 . | Daily Windows 1.0용 Arc Browser가 3개월 만에 공식적으로 GA Windows 10 시장 점유율이 70%에 도달했으며 Windows 11 GitHub는 AI 기본 개발 도구 GitHub Copilot Workspace JAVA를 계속해서 출시했습니다 . OLTP+OLAP을 처리할 수 있는 유일한 강력한 유형의 쿼리입니다. 우리는 너무 늦게 만났습니다 .