저자: 유 팬
배경
신경망 아키텍처의 발전 역사를 되돌아보면 대칭은 항상 숨겨진 핵심 역할을 했으며, 기하학적 딥러닝은 대칭의 중요성을 강조한다는 것을 알 수 있습니다. 한편, 전통적인 컴퓨터 비전과 자연어 처리 분야에서 우리는 Transformer 기반의 네트워크 아키텍처가 최근 몇 년 동안 놀라운 결과를 달성했다는 것을 확인했습니다. 한편, 대칭은 첫 번째 원리로서 자연과학에서 중요한 역할을 합니다. 따라서 대칭의 관점에서 볼 때 기하학적 딥러닝이 인공지능과 과학의 결합에서 중요한 역할을 할 것이라고 믿을 만한 이유가 있습니다.
그림 1: 인공지능과 과학 분야의 기하학적 딥러닝 결합
실제로 심층 기하학 학습은 과학용 AI 분야에서 인상적인 결과를 얻었으며 점점 더 중요한 역할을 할 것입니다. 그래프 신경망과 Transformer를 기반으로 한 Alphafold2는 단백질 구조 예측에 있어 매우 높은 정확도를 보여줍니다. 소분자 구조의 예측 및 생성에서 유클리드 공간의 추가 강체 변환 대칭(E(3) 대칭 그룹)을 그래프 신경망에 추가하면 계산 정확도가 크게 향상되고 훈련 복잡성이 줄어들 수 있습니다. 지구기상 예측에서는 지구 표면이 2차원 구이기 때문에 다양체에 대한 컨볼루션, 좌표 지정 변환 등의 문제가 수반되며, 기하학적 딥러닝은 신경망 설계를 위한 체계적인 이론적 틀을 제공합니다. 우주론에서는 중력으로 인해 공간과 시간이 휘어지며, 기하학적 딥러닝은 이러한 휘어진 리만 다양체 구조와 AI의 결합에 대한 이론적 기반을 제공합니다.
반면, 응집물질물리학, 양자물리학 등 기초과학 분야에서는 아직 AI와의 융합 정도가 깊지 않다. 이들 분야에서는 인간의 체계적 이론 지식이 비교적 잘 발달되어 있지만, 고품질의 데이터를 얻기가 매우 어렵기 때문이다. 따라서 알려진 지식을 신경망에 "주입"하고 데이터 활용도를 향상시키는 방법이 특히 중요합니다.
그룹 등변 신경망은 데이터 활용도를 향상시키는 데 놀라운 이점을 보여주었습니다. 예를 들어 3차원 테트리스의 분류 작업에는 총 8개의 구성이 있습니다. 전통적인 접근 방식은 데이터 향상을 위해 각 데이터 구성의 공간적 회전을 많이 필요로 하며, 이는 의심할 여지 없이 데이터 양과 훈련의 복잡성을 크게 증가시키고 예측 정확도를 보장할 수 없습니다. E(3) 등변 신경망에서 각 구성에는 하나의 데이터만 필요하며, E(3) 변환을 통해 두 구성을 연결할 수 있는 경우에는 더 적은 데이터만 필요합니다. 필요한 데이터의 양을 크게 줄 이면서 이론적 수준에서 예측 정확도가 보장되는 동시에 이 신경망은 더 나은 해석 가능성 과 표현 능력을 갖추고 있습니다 .
알려진 모든 지식 중에서 대칭은 심오하고 기본적인 지식 유형이며, 자연의 법칙을 설명하는 열쇠이기도 합니다. 예를 들어 고에너지 입자의 시공간은 로렌츠군대칭(SO(1, 3)군)을 가지며, 로렌츠군 등변 신경망은 향후 고에너지 물리학에서 중요한 역할을 할 수 있다. 현대 물리학은 장 이론을 사용하여 설명되며, 그 뒤에 있는 수학적 언어도 미분 기하학과 섬유 다발입니다. 현대 물리학과 인공 지능의 결합에서 심층 기하학 학습이 주도적인 역할을 할 것으로 예상됩니다.
기하학적 딥러닝을 기반으로 한 대규모 AI for Science 모델의 경우 간단하고 대담한 아이디어를 만들 수 있습니다. 먼저 대칭군의 거짓말 대수 방법을 학습하는 것과 같은 일종의 신경망을 통해 입력 시스템의 대칭성을 학습합니다. 3] 그런 다음 특정 메커니즘을 통해 다양한 대칭의 강도를 제어하여 네트워크가 사용할 등변 네트워크의 대칭 그룹을 선택할 수 있도록 하여 네트워크가 입력 시스템의 대략적인 대칭을 충족할 수 있습니다. 물론, 미래의 대규모 모델은 그렇게 간단하지 않을 가능성이 높으며, 아직 해결되지 않은 문제도 가득하기 때문에 앞으로 이 방향으로 더 많은 진전이 있기를 기대합니다.
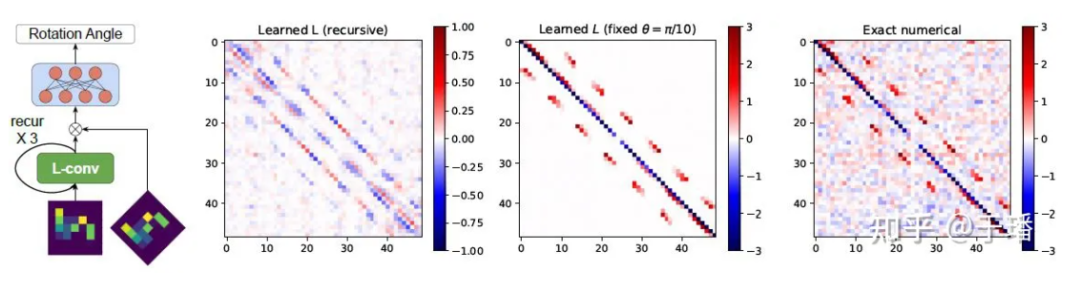
그림 2: L-conv 학습 데이터의 SO(2) 그룹에 대한 거짓말 대수
참고자료
[1] 브론스타인, 마이클 M., 그 외 여러분. "기하학적 딥 러닝: 그리드, 그룹, 그래프, 측지선 및 게이지." arXiv 사전 인쇄 arXiv:2104.13478 (2021).
[2] 와일러(Weiler), 모리스(Maurice), 그 외 여러분. "독립 컨볼루션 네트워크 조정 - 리만 다양체의 등변성 컨볼루션 및 게이지 등변 컨볼루션." arXiv 사전 인쇄 arXiv:2106.06020 (2021).
[3] Dehmamy N, Walters R, Liu Y, 외. 거짓말 대수 컨벌루션 네트워크[J]를 이용한 자동 대칭 발견. 신경 정보 처리 시스템의 발전, 2021, 34: 2503-2515.
1990년대에 태어난 프로그래머가 비디오 포팅 소프트웨어를 개발하여 1년도 안 되어 700만 개 이상의 수익을 올렸습니다. 결말은 매우 처참했습니다! Google은 Flutter, Dart 및 Python 팀의 중국 코더의 "35세 저주"와 관련된 정리해고를 확인했습니다 . | Daily Windows 1.0용 Arc Browser가 3개월 만에 공식적으로 GA Windows 10 시장 점유율이 70%에 도달했으며 Windows 11 GitHub는 AI 기본 개발 도구 GitHub Copilot Workspace JAVA를 계속해서 출시했습니다 . OLTP+OLAP을 처리할 수 있는 유일한 강력한 유형의 쿼리입니다. 우리는 너무 늦게 만났습니다 .
