문학 재귀 적으로 해결!

머리말

재귀 알고리즘은 응용 프로그램이 매우 광범위한 구글이 볼 수있는 대형으로 페이지 랭크 (PageRank) 알고리즘, 팩토리얼 작고 통계적 파일로 다음 작업 폴더 크기에 사용되는 매우 중요한 개념이다, 면접관의 아주 좋아 하더군요 테스트 사이트

최근 많은 기사 재귀를 읽고 많은 것을 배웠습니다,하지만 대부분의 온라인 기사 말하는 재귀 덜 포괄적 발견, 주요 문제는 문제 해결의 대부분 제공되지 않습니다 적절한 시간 / 공간의 복잡성은, 알고리즘의 시간 / 공간의 복잡성은 우리가 재귀 알고리즘의 복잡성을 해결할 수있는 경우 재귀 알고리즘의 중요한 고려 사항! 시간 복잡도는, 즉, 일반적으로 다른 알고리즘 제목 제목의 시간 복잡도 (사용 유도 등 필요) 더 어렵다입니다 도 기본적으로 혼자. 또한, 그들 중 많은 시간 재귀 알고리즘의 복잡성이 발견을 통해 계산 된 시간 복잡도, 당신은 변환 아이디어를 필요로하는 경우, 더 나은 솔루션이 있는지 봐 가지고, 허용되지 않습니다,이되지 재귀 및 재귀에 대한 근본적인 목적이다 !

이 논문의 시도는 다음과 같은 측면이 재귀 설명하기

1. 재귀는 무엇입니까?
2. 재귀 알고리즘 범용 솔루션
3. (주부터 높은 순서) 실천 운동

우리가 특히 본질적으로 재귀 것, 재귀인지 새로운 수준의 성능에 노력하자 재귀 시간 복잡도를 해결하기 위해 당신에게 루틴의 매우 일반적인 개요를 제공합니다 상세한 분석의 시간 복잡도를, 당신은 확실히 읽을 생각 수확

무엇 재귀

이 현상은 재귀 호출, 함수에 함수 자체를 호출하는 경우가 있습니다 경우 간단히했습니다.

계승 계승 기능의 존재 하에서 예로서 계층 기능, 다음 - 전화 (1 N), 그래서이 기능은 재귀 함수임을

public int factorial(int n) {
    if (n < =1) {
        return 1;
    }
    return n * factorial(n - 1)
}

추가 분석 "순환"최초 "전송"을 선택하고있다 "정규화"되며, 서브 문제로 분해 문제는 해결할 수 있음 "전달"수단이 분해 될 때까지 ... 서브 - 서브 - 서브 문제로 분류 문제 미세한 하위 문제로 하위 문제가 더 이상 분할 (즉, 해결 될 수있다)이 "반환"그 때 해결 될 것입니다 하위 문제의 층이다, 가장 하위 문제가 해결 말하고, 문제의 하위 계층은 해결하기 그리고 위 하위 문제는 문제가 시작 매우 해결 될 때까지 우리는 클래스 F "배달"의 예로서 그것에 (6) 볼 필요가 텍스트가 조금 추상적 일 수있다, ..., 자연적으로 해결 될 것입니다 "정상화."

F (6) = N * F 이후 문제점 F (6)을 해결 (5), 그래서 F (6) F로 분해 할 필요가 있음 (5) 서브 문제가 해결 마찬가지로 (5) 바. = N * F (4 )뿐만 아니라, F (2) 2 (F) (= 때문에, F (1)을 해결하기 위해 "손"인 상기 분할 ... F까지 (1)에 1) = 2 또한 해결된다 .. ... F (N)가 마침내 해결 방법이있는 문제의 재귀 적 성격이 가지고 분할을 할 수 있도록, "이동" 상기와 같은 문제점을 해결하기 위하여 동일한 아이디어를 하위 문제. . . 마지막 하위 문제가 더 이상 분해 분할이 하위 문제는 본질적으로 '정상화'의 과정에서, 최소 크기 후 해결 될 수 해결 될 때까지 가장 일반적인 문제는 시작 해결하기 위해 자연적으로 온다.

재귀 알고리즘 범용 솔루션

재귀 무엇의주의 깊은 분석에 우리는 재귀는 다음과 같은 두 가지 특징에서 찾을 수 있습니다

1. 한 가지 문제가에 침입했을 수 있습니다 상기와 같은 문제점을 해결하기 위하여 같은 아이디어 하위 문제를, 하위 하위 문제, 즉이 문제는 동일한 기능을 호출 할 수 있습니다
2. 하위 문제 분해 분해 (즉, 종료 조건) 될 수없는 고정 된 값을 가지고 있어야 층을 통해 마지막 아니라 분해 하위 문제 끝없이 문제 해결책이 명확하지 않는 경우.

주요 질문 재귀 솔루션입니다 그래서 그 피사체가 두 개 이상의 재귀의 솔루션 특성에 따라 판단 할 수 있는지 여부에 사용 재귀에 우리 첫째가 필요합니다.

판사가 재귀를 사용할 수 있습니다 후, 우리는 기본적인 문제 해결 재귀 루틴 (네 단계)를 살펴 :

1. 함수 정의 이 함수 명확 재귀이 함수 자체를 호출 문제 서브 문제점을 특징으로하기 때문에,이 함수의 기능이 결정되면 있도록 문제 서브 문제 재귀 관계 일 수에 대한 긴 검색하면,
2. 그런 문제점 및 서브 문제 (즉, 관계를 찾아 재발 화학식 정도로 인해 서브 문제에 문제가)가 동일한 용액 아이디어 만큼 서브 문제 정의 된 함수 호출이 1 단계로서, 문제가 해결 될 수있다. 다음은 화학식 같은 아웃, 그 관계의 최선이 될 수 소위 F (N) = N * F (N-) 때문에, 의사 코드 표현을 사용하여, 투명한 화학식 그릴 일시적없는는 점화식의 FOUND 후, 또한 가능하다면 결국 더 이상 (중태), 고장없는 아이의 문제의 해결책을 찾기 위해 그 문제가 분해 제한이없는 서브를 할 수 있도록. 이 기능의 제 1 단계가 정의 된 바와 같이, 서브 문제가 있으므로 분할 문제의 서브 문제 단계 1에서 정의 된 함수, 재귀 호출받을 수 (호출 함수 자체)
3. 재귀 식의 두 번째 단계는에 의해 정의 된 코드에 추가하는 단계를 나타내는 함수
4. 마지막으로 중요한 단계, 하위 문제와의 관계에 따라 시간 복잡도 추론, 경우 복잡성은 받아 들일 재귀 시간을 찾아, 당신은 할 필요가 아이디어를 변환하는 변환 더 신뢰할 수있는 솔루션이 있는지, 보라

사운드의 단순, 우리는 몇 재귀 문제에서의 모습을 찾기 위해 진보적 인 접근을 설정 방법은 위의 몇 가지 단계

(주부터 높은 순서) 실천 운동

워밍업 경기

양의 정수 n을 출력 N! 값을 입력합니다. 상기 N-! 1 = 2 . 3 ... N- 즉 계승

그것을 수행하는 방법을 찾기 위해 우리는 4 단계 문제 해결 재귀 루틴에 대해 얘기 한 적용

1. 이 기능은이 기능의 명확한, 우리는이 함수는 다음 구걸, N-1을 N의 계승을 찾는 것입니다 알고, 정의, N-2 계승는에이 함수를 호출 할 수 있습니다

/**
 * 求 n 的阶乘
 */
public int factorial(int n) {
}

문제와 자식 관계의 문제 찾기 2.
관계 계승하는 비교적 간단하고, 우리는 F (n)이 명백하게 (N) F, N의 계승을 나타내는가 = N * F (N - 1), 임계 조건 F 동안 (1) = 1, 즉

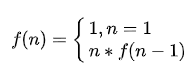
3 단계의 반복 화학식은 스텝 함수에 의해 정의 된 코드로 표시되는 추가

/**
 * 求 n 的阶乘
 */
public int factorial(int n) {
    // 第二步的临界条件
    if (n < =1) {
        return 1;
    }

    // 第二步的递推公式
    return n * factorial(n-1)
}

4. 시간 복잡도 시크
F (N) 이후를 = N * F (N-1) = N * (N-1) * ... * F (1), N 체배 시간 복잡도 총 제조 그것은 N입니다.

물론,이 질문은 정말 너무 간단 외모없는 그런 지점이있을 나타납니다, 그것은, 우리는 약간의 고급 주제를 쉽게 일상 보면됩니다

항목 제목

一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶，例如：

점프를 직접 레벨 1 : 레벨 1에서 점프는 한 단계 점프입니다.
하나 또는 두 가지를 건너 1 각 건너 뛰기, 두 번 점프 : 레벨 2 점프 점프 방법은 두 가지 단계가 있습니다.
나는 얼마나 많은 점프 단계 N 단계 점프하도록 요청?

우리는 어떻게 일상에서 4 단계의 모습을 계속 누릅니다

제 n 스테이지 점프 점프 방법의 단계를 나타내는 함수를 정의 1.

/**
 * 跳 n 极台阶的跳法
 */
public int f(int n) {
}

이전 관계 문제 및 하위 문제를 찾습니다

첫눈에 두 전에이 관계는 단서가 표시되지 않지만, 주제에 면밀한 관찰이 개구리는 한 단계 또는 두 단계, 이동할 수 있습니다 위에서 아래로 생각 n을 계단 만 건너 뛰려면 말을하는 것입니다, 제 n-1 또는 n-2 레벨로부터 이동 문제 점프 N-1, N-2 수준 단계 점프 방식으로 변화되고,
F (n)의 계단 대표은 다음 점프 수단을 이동한다면 상기 분석 결과, 우리는 관계 문제 및 서브 문제 (N F (N) = F를 얻을 수입니다 찾는 것이 분명 -1) + F (N-2), 분명하게 될 때, N = 1, N = 2, 즉 점프 열두 공정 문제에 대한 최종 솔루션, 이렇게 순환 식의 시스템

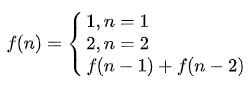
3 단계의 반복 화학식 첨가 기능 코드로 1 단계로 정의하여 표현
보충제로서 기능

/**
 * 跳 n 极台阶的跳法
 */
public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n-1) + f(n-2)
}

4. 계산시 복잡도
를 상기 분석에서 명백한
F (n)은 다음 식을 만족

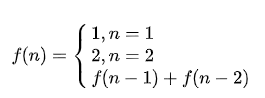
고급 대수와 관련된 컴퓨팅 기술의 피보나치 시간 복잡도는,하지를 추론 세부 사항이, 관심있는 학생들은 클릭 할 수 있습니다 여기 보고, 우리가 직접 결론을 부담

이들은 시간 복잡도 알 수있다 지수 레벨은 명백하게 용인, 너무 높은 이유를 생각해 보면 그 시간 복잡도, 우리는 다음과 같다, 상기 유도 재귀 공식에 따라 계산 된 F (6)한다고 가정

(N)의 증가에 따라, 세 번 계산되고 반복 계산의 다수, F (3)를 볼 수 있으며, 시간의 F (n)은 기하 급수적으로 증가 NATURAL

5. 최적화
만남 중간 상태 후 계산하면 많은 이중 계산이 있기 때문에, 우리가 함께 이러한 중간 계산 결과를 저장할 생각할 수는 직접 쿼리를 저장 한 결과이있을 수 계산하기 위해 필요 이것은 전형적인 시간 공간 코드의 변화가 다음과 같이 후,

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    // map 即保存中间态的键值对， key 为 n，value 即 f(n)
    if (map.get(n)) {
        return map.get(n)
    }
    return f(n-1) + f(n-2)
}

그런 변형의 시간 복잡도는 어느 정도의 시간 복잡도는 O (n)을하므로, 각 F (N) 우리는 중간 상태를 저장할 수있는 어떠한 이중 계산이없는 계산으로 만, 사용 이후 인 공간 복잡도는 O (n)을하므로 키 - 값 쌍의 중간 결과를 유지한다. 여기서 문제는 이미 해결 된 것으로 간주되지만 프로그래머의 추구로, 우리는 아직도 물어 봐야, 당신은 공간의 복잡성을 최적화하기 위해 계속 할 수 있습니까?

5. 루프 반복 알고리즘 변환
분석 문제점 및 하위 문제 관계 ( F (N-) = F (N-- 1) + F (N -. 2) )를 사용하는 경우 하향식 분석 형태이지만 사실, 우리는 용액 F (N)을 할 때 사용할 수있는 상향식 (bottom-up) 접근을 해결하기 위해, 우리는 다음과 같은 규칙을 관찰함으로써 알 수 있습니다

f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 5
....
f(n) = f(n-1) + f(n-2)

(F)의 최저치 (1), F (2) F (3), F (4) 이후, ... 문제 같은는 F (N) 때까지 처음 두 따라 해결 될 수 결정된다. 우리의 코드는 다음과 같은 방법으로 변환 할 수 있도록

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;

    int result = 0;
    int pre = 1;
    int next = 2;
    
    for (int i = 3; i < n + 1; i ++) {
        result = pre + next;
        pre = next;
        next = result;
    }
    return result;
}

우리는 공간 복잡도는 O이고 그래서, (1) 두 변수 (다음, 사전)을 정의하기 때문에 변환 후, 시간 복잡도는 O (n)은, 상기 연산 처리에

简单总结一下： 分析问题我们需要采用自上而下的思维，而解决问题有时候采用自下而上的方式能让算法性能得到极大提升,思路比结论重要

初级题

接下来我们来看下一道经典的题目: 反转二叉树
将左边的二叉树反转成右边的二叉树

接下来让我们看看用我们之前总结的递归解法四步曲如何解题

1.定义一个函数，这个函数代表了 翻转以 root 为根节点的二叉树

public static class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public TreeNode invertTree(TreeNode root) {
}

2.查找问题与子问题的关系,得出递推公式
我们之前说了，解题要采用自上而下的思考方式，那我们取前面的1， 2，3 结点来看，对于根节点 1 来说，假设 2, 3 结点下的节点都已经翻转，那么只要翻转 2， 3 节点即满足需求

对于2， 3 结点来说，也是翻转其左右节点即可,依此类推,对每一个根节点，依次翻转其左右节点，所以我们可知问题与子问题的关系是
翻转(根节点) = 翻转(根节点的左节点) + 翻转(根节点的右节点)
即
invert(root) = invert(root->left) + invert(root->right)

而显然递归的终止条件是当结点为叶子结点时终止（因为叶子节点没有左右结点）

3.将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中

 public TreeNode invertTree(TreeNode root) {
    // 叶子结果不能翻转
    if (root == null) {
        return null;
    }
    // 翻转左节点下的左右节点
    TreeNode left = invertTree(root.left);
    // 翻转右节点下的左右节点
    TreeNode right = invertTree(root.right);

    // 左右节点下的二叉树翻转好后，翻转根节点的左右节点
    root.right = left;
    root.left = right;
    return root;
}

4.时间复杂度分析
由于我们会对每一个节点都去做翻转，所以时间复杂度是 O(n)，那么空间复杂度呢，这道题的空间复杂度非常有意思，我们一起来看下，由于每次调用 invertTree 函数都相当于一次压栈操作， 那最多压了几次栈呢， 仔细看上面函数的下一段代码

    TreeNode left = invertTree(root.left);

从根节点出发不断对左结果调用翻转函数, 直到叶子节点，每调用一次都会压栈，左节点调用完后，出栈，再对右节点压栈....,下图可知栈的大小为3， 即树的高度，如果是完全二叉树 ，则树的高度为logn, 即空间复杂度为O(logn),

最坏情况，如果此二叉树是如图所示(只有左节点，没有右节点)，则树的高度即结点的个数 n，此时空间复杂度为 O(n),总的来看，空间复杂度为O(n)

说句题外话，这道题当初曾引起轰动，因为 Mac 下著名包管理工具 homebrew 的作者 Max Howell 当初解不开这道题，结果被 Google 拒了，也就是说如果你解出了这道题，就超越了这位世界大神，想想是不是很激动

中级题

接下来我们看一下大学时学过的汉诺塔问题：
　　如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

接下来套用我们的递归四步法看下这题怎么解

1.定义问题的递归函数，明确函数的功能,我们定义这个函数的功能为：把 A 上面的 n 个圆盘经由 B 移到 C

// 将 n 个圆盘从 a 经由 b 移动到 c 上
public void hanoid(int n, char a, char b, char c) {
}

2.查找问题与子问题的关系
首先我们看如果 A 柱子上只有两块圆盘该怎么移

前面我们多次提到，分析问题与子问题的关系要采用自上而下的分析方式，要将 n 个圆盘经由 B 移到 C 柱上去，可以按以下三步来分析
* 将 上面的 n-1 个圆盘看成是一个圆盘,这样分析思路就与上面提到的只有两块圆盘的思路一致了
* 将上面的 n-1 个圆盘经由 C 移到 B
* 此时将 A 底下的那块最大的圆盘移到 C
* 再将 B 上的 n-1 个圆盘经由A移到 C上

有人问第一步的 n - 1 怎么从 C 移到 B,重复上面的过程,只要把 上面的 n-2个盘子经由 A 移到 B, 再把A最下面的盘子移到 C,最后再把上面的 n - 2 的盘子经由A 移到 B 下..., 怎么样，是不是找到规律了，不过在找问题的过程中 切忌把子问题层层展开,到汉诺塔这个问题上切忌再分析 n-3,n-4 怎么移，这样会把你绕晕，只要找到一层问题与子问题的关系得出可以用递归表示即可。

由以上分析可得

move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C`)

一定要先得出递归公式，哪怕是伪代码也好!这样第三步推导函数编写就容易很多，终止条件我们很容易看出，当 A 上面的圆盘没有了就不移了

3.根据以上的递归伪代码补充函数的功能

// 将 n 个圆盘从 a 经由 b 移动到 c 上
public void hanoid(int n, char a, char b, char c) {
    if (n <= 0) {
        return;
    }
    // 将上面的  n-1 个圆盘经由 C 移到 B 
    hanoid(n-1, a, c, b);
    // 此时将 A 底下的那块最大的圆盘移到 C
    move(a, c);
    // 再将 B 上的 n-1 个圆盘经由A移到 C上
    hanoid(n-1, b, a, c);
}

public void move(char a, char b) {
    printf("%c->%c\n", a, b);
}

从函数的功能上看其实比较容易理解，整个函数定义的功能就是把 A 上的 n 个圆盘 经由 B 移到 C，由于定义好了这个函数的功能，那么接下来的把 n-1 个圆盘 经由 C 移到 B 就可以很自然的调用这个函数,所以明确函数的功能非常重要,按着函数的功能来解释，递归问题其实很好解析，切忌在每一个子问题上层层展开死抠,这样这就陷入了递归的陷阱，计算机都会栈溢出，何况人脑

4.时间复杂度分析
从第三步补充好的函数中我们可以推断出

f(n) = f(n-1) + 1 + f(n-1) = 2f(n-1) + 1
= 2(2f(n-2) + 1) + 1 = 2 * 2 * f(n-2) + 2 + 1 = 2² * f(n-3) + 2 + 1
= 2² * f(n-3) + 2 + 1 = 2² * (2f(n-4) + 1) = 2³ * f(n-4) + 2² + 1
= .... // 不断地展开
= 2^n-1 + 2^n-2 + ....+ 1

显然时间复杂度为 O(2ⁿ)，很明显指数级别的时间复杂度是不能接受的，汉诺塔非递归的解法比较复杂，大家可以去网上搜一下

进阶题

现实中大厂中的很多递归题都不会用上面这些相对比较容易理解的题，更加地是对递归问题进行相应地变形， 来看下面这道题

细胞分裂 有一个细胞 每一个小时分裂一次，一次分裂一个子细胞，第三个小时后会死亡。那么n个小时候有多少细胞？

照样我们用前面的递归四步曲来解

1.定义问题的递归函数，明确函数的功能
我们定义以下函数为 n 个小时后的细胞数

public int allCells(int n) {
}

2.接下来寻找问题与子问题间的关系（即递推公式）
首先我们看一下一个细胞出生到死亡后经历的所有细胞分裂过程

图中的 A 代表细胞的初始态, B代表幼年态(细胞分裂一次), C 代表成熟态(细胞分裂两次)，C 再经历一小时后细胞死亡
以 f(n) 代表第 n 小时的细胞分解数
f_a(n) 代表第 n 小时处于初始态的细胞数,
f_b(n) 代表第 n 小时处于幼年态的细胞数
f_c(n) 代表第 n 小时处于成熟态的细胞数
则显然 f(n) = f_a(n) + f_b(n) + f_c(n)
那么 f_a(n) 等于多少呢，以n = 4 （即一个细胞经历完整的生命周期）为例

仔细看上面的图

可以看出
f_a(n) = f_a(n-1) + f_b(n-1) + f_c(n-1), 当 n = 1 时，显然 f_a(1) = 1

f_b(n) 呢,看下图可知 f_b(n) = f_a(n-1)。 当 n = 1 时 f_b(n) = 0

f_c(n) 呢,看下图可知 f_c(n) = f_b(n-1)。当 n = 1,2 时 f_c(n) = 0

综上， 我们得出的递归公式如下

f(n) = f_a(n) + f_b(n) + f_c(n)

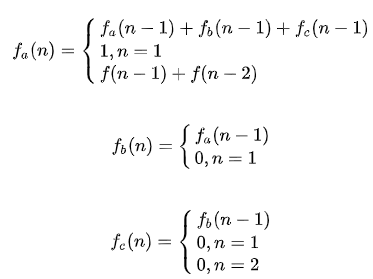
3.根据以上的递归公式我们补充一下函数的功能

public int allCells(int n) {
    return aCell(n) + bCell(n) + cCell(n);
}

/**
 * 第 n 小时 a 状态的细胞数 
 */
public int aCell(int n) {
    if(n==1){
        return 1;
    }else{
        return aCell(n-1)+bCell(n-1)+cCell(n-1);
    }
}

/**
 * 第 n 小时 b 状态的细胞数 
 */
public int bCell(int n) {
    if(n==1){
        return 0;
    }else{
        return aCell(n-1);
    }
}

/**
 * 第 n 小时 c 状态的细胞数 
 */
public int cCell(int n) {
    if(n==1 || n==2){
        return 0;
    }else{
        return bCell(n-1);
    }
}

只要思路对了，将递推公式转成代码就简单多了，另一方面也告诉我们，可能一时的递归关系我们看不出来，此时可以借助于画图来观察规律

4.求时间复杂度
由第二步的递推公式我们知道
f(n) = 2aCell(n-1) + 2aCell(n-2) + aCell(n-3)

之前青蛙跳台阶时间复杂度是指数级别的，而这个方程式显然比之前的递推公式(f(n) = f(n-1) + f(n-2)) 更复杂的，所以显然也是指数级别的

总结

大部分递归题其实还是有迹可寻的， 按照之前总结的解递归的四个步骤可以比较顺利的解开递归题，一些比较复杂的递归题我们需要勤动手，画画图，观察规律，这样能帮助我们快速发现规律，得出递归公式，一旦知道了递归公式，将其转成递归代码就容易多了,很多大厂的递归考题并不能简单地看出递归规律，往往会在递归的基础上多加一些变形，不过万遍不离其宗，我们多采用自顶向下的分析思维，多练习，相信递归不是什么难事

公众号「码海」，欢迎关注！