Descreva resumidamente vários algoritmos de classificação comumente usados

Abstract: Merge sort e quick sort são dois algoritmos de ordenação um pouco complicados. Ambos usam a ideia de dividir e conquistar. Os códigos são implementados por meio de recursão e o processo é muito semelhante. A chave para entender a classificação por mesclagem é entender a fórmula de recursão e a função de mesclagem merge().

Este artigo é compartilhado pela comunidade de nuvem da Huawei " Oito algoritmos de classificação de maneiras simples ", autor: Embedded Vision.

Merge sort e quick sort são dois algoritmos de classificação um pouco complicados. Ambos usam a ideia de dividir e conquistar, e o código é implementado por meio de recursão. O processo é muito semelhante. A chave para entender a classificação por mesclagem é entender a fórmula de recursão e a função de mesclagem merge().

Um, tipo de bolha (Bubble Sort)

Algoritmo de ordenação é um tipo de algoritmo que os programadores devem entender e estar familiarizados.Existem muitos tipos de algoritmos de ordenação, tais como: bolhas, inserção, seleção, rápido, fusão, contagem, cardinalidade e ordenação de balde.

A classificação por bolha só funcionará em dois dados adjacentes. Cada operação de borbulhamento irá comparar dois elementos adjacentes para ver se eles atendem aos requisitos de relação de tamanho e, se não, permitir que sejam trocados. Um borbulhamento moverá pelo menos um elemento para onde deveria estar e repetirá n vezes para concluir a classificação de n dados.

Resumo: Se o array tiver n elementos, no pior caso, serão necessárias n operações de borbulhamento.

O código C++ do algoritmo básico de classificação por bolhas é o seguinte:

// 将数据从小到大排序
void bubbleSort(int array[], int n){
 if (n<=1) return;
 for(int i=0; i<n; i++){
 for(int j=0; j<n-i; j++){
 if (temp > a[j+1]){
                temp = array[j]
                a[j] = a[j+1];
                a[j+1] = temp;
 }
 }
 }
}

Na verdade, o algoritmo de classificação de bolhas acima também pode ser otimizado. Quando uma determinada operação de bolha não realiza mais a troca de dados, isso significa que a matriz já está em ordem e não há necessidade de continuar a executar as operações de bolha subsequentes. O código otimizado é o seguinte:

// 将数据从小到大排序
void bubbleSort(int array[], int n){
 if (n<=1) return;
 for(int i=0; i<n; i++){
 // 提前退出冒泡循环发标志位
        bool flag = False;
 for(int j=0; j<n-i; j++){
 if (temp > a[j+1]){
                temp = array[j]
                a[j] = a[j+1];
                a[j+1] = temp;
                flag = True; // 表示本次冒泡操作存在数据交换
 }
 }
 if(!flag) break; // 没有数据交换，提交退出
 }
}

Características do Bubble Sort :

1. O processo de borbulhamento envolve apenas a troca de elementos adjacentes e requer apenas um nível constante de espaço temporário, portanto a complexidade do espaço é O(1) O (1), que é um algoritmo de classificação no local .
2. Quando há dois elementos adjacentes do mesmo tamanho, não trocamos, e os dados do mesmo tamanho não mudarão a ordem antes e depois da classificação, portanto, é um algoritmo de classificação estável .
3. O pior caso e a complexidade de tempo média são O(n2) O ( n 2 ), e a melhor complexidade de tempo é O(n) O ( n ).

Em segundo lugar, classificação por inserção (Insertion Sort)

1. O algoritmo de classificação por inserção divide os dados na matriz em dois intervalos: o intervalo classificado e o intervalo não classificado. O intervalo classificado inicial possui apenas um elemento, que é o primeiro elemento da matriz.
2. A ideia central do algoritmo de classificação por inserção é pegar um elemento do intervalo não classificado, encontrar uma posição adequada para inserir no intervalo classificado e garantir que os dados no intervalo classificado estejam sempre em ordem.
3. Repita este processo até que os elementos do intervalo não classificados estejam vazios, então o algoritmo termina.

A classificação por inserção, como a classificação por bolha, também inclui duas operações, uma é a comparação de elementos e a outra é o movimento de elementos .

Quando precisamos inserir um dado a no intervalo classificado, precisamos comparar o tamanho de a com os elementos do intervalo classificado para encontrar uma posição de inserção adequada. Depois de encontrar o ponto de inserção, também precisamos mover a ordem dos elementos após o ponto de inserção um bit para trás, de modo a abrir espaço para a inserção do elemento a.

A implementação do código C++ da ordenação por inserção é a seguinte:

void InsertSort(int a[], int n){
 if (n <= 1) return;
 for (int i = 1; i < n; i++) // 未排序区间范围
 {
        key  = a[i]; // 待排序第一个元素
        int j = i - 1; // 已排序区间末尾元素
 // 从尾到头查找插入点方法
 while(key < a[j] && j >= 0){ // 元素比较
            a[j+1] = a[j]; // 数据向后移动一位
            j--;
 }
        a[j+1] = key; // 插入数据
 }
}

Recursos de classificação por inserção:

1. A classificação por inserção não requer espaço de armazenamento adicional e a complexidade do espaço é O(1) O (1), portanto, a classificação por inserção também é um algoritmo de classificação no local.
2. Na classificação por inserção, para elementos com o mesmo valor, podemos optar por inserir os elementos que aparecem depois na parte de trás dos elementos que aparecem antes, para que a ordem original da frente e de trás possa ser mantida inalterada, de modo que a classificação por inserção seja estável algoritmo de ordenação.
3. O pior caso e a complexidade de tempo média são O(n2) O ( n 2 ), e a melhor complexidade de tempo é O(n) O ( n ).

Três, classificação por seleção (Classificação por seleção)

A ideia de implementação do algoritmo de classificação por seleção é um pouco semelhante à classificação por inserção e também é dividida em intervalos classificados e intervalos não classificados. Mas a classificação de seleção sempre encontrará o menor elemento do intervalo não classificado e o colocará no final do intervalo classificado.

A complexidade de tempo do melhor caso, pior caso e caso médio de classificação por seleção é O(n2) O ( n 2), que é um algoritmo de classificação no local e um algoritmo de classificação instável .

O código C++ para ordenação por seleção é implementado da seguinte forma:

void SelectSort(int a[], int n){
 for(int i=0; i<n; i++){
        int minIndex = i;
 for(int j = i;j<n;j++){
 if (a[j] < a[minIndex]) minIndex = j;
 }
 if (minIndex != i){
            temp = a[i]; 
            a[i] = a[minIndex];
            a[minIndex] = temp;
 }
 }
}

Resumo da classificação da seleção de inserção de bolha

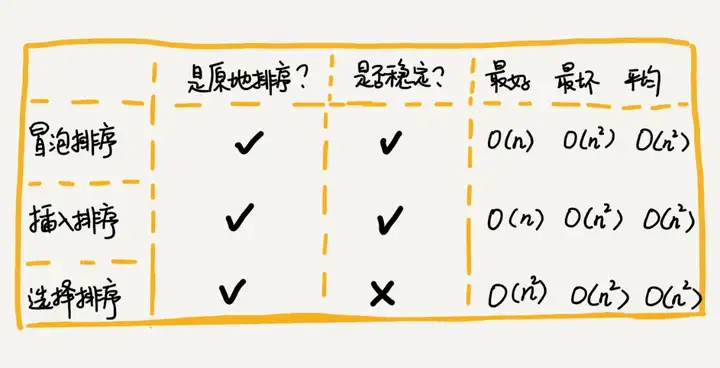
Os códigos de implementação desses três algoritmos de classificação são muito simples e muito eficientes para classificar dados de pequena escala. No entanto, ao classificar dados de grande escala, a complexidade de tempo ainda é um pouco alta, portanto, é mais provável usar um algoritmo de classificação com uma complexidade de tempo de O(nlogn) O ( nlogn ).

Certos algoritmos dependem de certas estruturas de dados. Os três algoritmos de classificação acima são todos implementados com base em arrays.

Quarto, classificação por mesclagem (Merge Sort)

A ideia central do merge sort é relativamente simples. Se quisermos classificar uma matriz, primeiro dividimos a matriz em partes frontal e traseira a partir do meio, depois classificamos as partes frontal e traseira separadamente e, em seguida, mesclamos as duas partes classificadas , para que toda a matriz esteja em ordem.

Merge sort usa a ideia de dividir e conquistar. Dividir e conquistar, como o nome sugere, é dividir e conquistar, decompondo um grande problema em pequenos subproblemas a serem resolvidos. Quando os pequenos subproblemas são resolvidos, o grande problema também é resolvido.

A ideia de dividir e conquistar é um pouco semelhante à ideia recursiva, e o algoritmo de dividir e conquistar geralmente é implementado com recursão. Dividir e conquistar é uma ideia de processamento para resolver problemas, e a recursão é uma técnica de programação, e as duas não entram em conflito.

Sabendo que a classificação por mesclagem usa o pensamento de dividir e conquistar, e o pensamento de dividir e conquistar geralmente é implementado usando recursão, o próximo foco é como usar a recursão para implementar a classificação por mesclagem . A habilidade de escrever código recursivo é analisar o problema para obter a fórmula recursiva, encontrar a condição de término e, finalmente, traduzir a fórmula recursiva em código recursivo. Portanto, se você deseja escrever o código para classificação por mesclagem, deve primeiro escrever a fórmula recursiva para classificação por mesclagem .

递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件：
p >= r 不用再继续分解，即区间数组元素为 1 

O pseudocódigo para classificação por mesclagem é o seguinte:

merge_sort(A, n){
 merge_sort_c(A, 0, n-1)
}
merge_sort_c(A, p, r){
 // 递归终止条件
 if (p>=r) then return
 // 取 p、r 中间的位置为 q
    q = (p+r)/2
 // 分治递归
 merge_sort_c(A[p, q], p, q)
 merge_sort_c(A[q+1, r], q+1, r)
 // 将A[p...q]和A[q+1...r]合并为A[p...r]  
 merge(A[p...r], A[p...q], A[q+1...r])
}

4.1, análise de desempenho de classificação de mesclagem

1. Merge sort é um algoritmo de classificação estável . Análise: A função merge_sort_c() no pseudocódigo apenas decompõe o problema e não envolve mover elementos e comparar tamanhos. A comparação de elementos reais e a movimentação de dados estão na parte da função merge(). No processo de mesclagem, é garantido que a ordem dos elementos com o mesmo valor permaneça inalterada antes e depois da mesclagem. A classificação por mesclagem é um algoritmo de classificação estável.

2. A eficiência de execução do merge sort não tem nada a ver com o grau de ordem do array original a ser classificado, então sua complexidade de tempo é muito estável. Seja o melhor caso, o pior caso ou o caso médio, o complexidade de tempo é O  ( nlogn) O ( nlogn ). Análise: Não apenas o problema de solução recursiva pode ser escrito como uma fórmula recursiva, mas a complexidade de tempo do código recursivo também pode ser escrita como uma fórmula recursiva:

3. A complexidade do espaço é O(n) . Análise: A complexidade do espaço do código recursivo não se soma como a complexidade do tempo. Embora cada operação de mesclagem do algoritmo precise solicitar espaço de memória adicional, após a conclusão da mesclagem, o espaço de memória temporariamente aberto é liberado. A qualquer momento, a CPU terá apenas uma função em execução e, portanto, apenas um espaço de memória temporário em uso. O espaço máximo de memória temporária não excederá o tamanho de n dados, portanto, a complexidade do espaço é O(n) O ( n ).

Cinco, classificação rápida (Quicksort)

A ideia do quicksort é a seguinte: se quisermos ordenar um conjunto de dados com subscritos de p a r no array, escolhemos qualquer dado entre p e r como pivô (ponto de partição ) . Percorremos os dados entre p e r, colocamos os dados menores que o pivô à esquerda, colocamos os dados maiores que o pivô à direita e colocamos o pivô no meio. Após esta etapa, os dados entre a matriz p e r são divididos em três partes. Os dados entre p e q-1 na frente são menores que o pivô, o meio é o pivô e os dados entre q+1 e r é maior que o pivô.

De acordo com a ideia de dividir e conquistar e recursão, podemos ordenar recursivamente os dados com subscritos de p a q-1 e os dados com subscritos de q+1 a r até que o intervalo seja reduzido a 1, o que significa que todos Os dados estão todos em ordem.

A fórmula de recursão é a seguinte:

递推公式：
quick_sort(p,r) = quick_sort(p, q-1) + quick_sort(q, r)
终止条件：
p >= r

Mesclar classificação e resumo de classificação rápida

Merge sort e quick sort são dois algoritmos de classificação um pouco complicados. Ambos usam a ideia de dividir e conquistar, e o código é implementado por meio de recursão. O processo é muito semelhante. A chave para entender a classificação por mesclagem é entender a fórmula de recursão e a função de mesclagem merge(). Da mesma forma, a chave para entender o quicksort é entender a fórmula recursiva, bem como a função de partição partition().

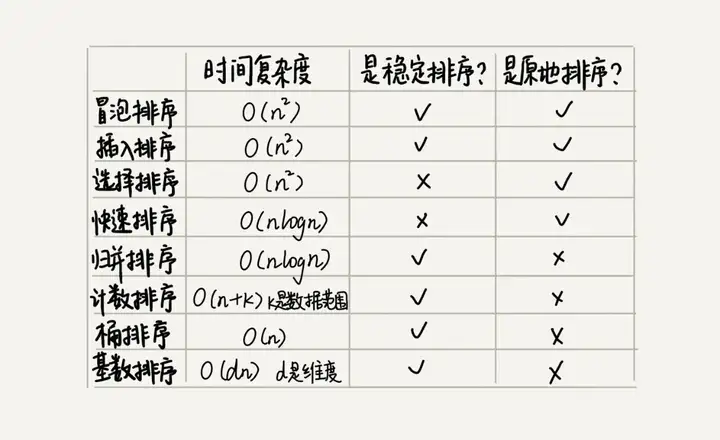
Além dos 5 algoritmos de classificação acima, existem 3 algoritmos de classificação linear cuja complexidade de tempo é O(n) O ( n ) : classificação de balde, classificação de contagem e classificação de base. O desempenho desses oito algoritmos de classificação é resumido na figura a seguir:

Referências

• Classificação (Parte 1): Por que a classificação por inserção é mais popular do que a classificação por bolha?
• Ordenação (abaixo): Como encontrar o K-ésimo maior elemento em O(n) com a ideia de ordenação rápida?

 

Clique para seguir e aprender sobre as novas tecnologias da Huawei Cloud pela primeira vez~

{{o.name}}

{{m.name}}