Aprendizado por reforço do ChatGPT, grande matador - otimização de estratégia proximal (PPO)

Aprendizado por reforço do ChatGPT, grande matador - otimização de estratégia proximal (PPO)

Proximal Policy Optimization ( Proximal Policy Optimization ) vem do artigo Proximal Policy Optimization Algorithms (Schulman et. al., 2017), que é atualmente o algoritmo de aprendizado por reforço (RL) mais avançado . Este algoritmo elegante pode ser usado para várias tarefas e tem sido aplicado em muitos projetos. O recentemente popular ChatGPT adotou este algoritmo.

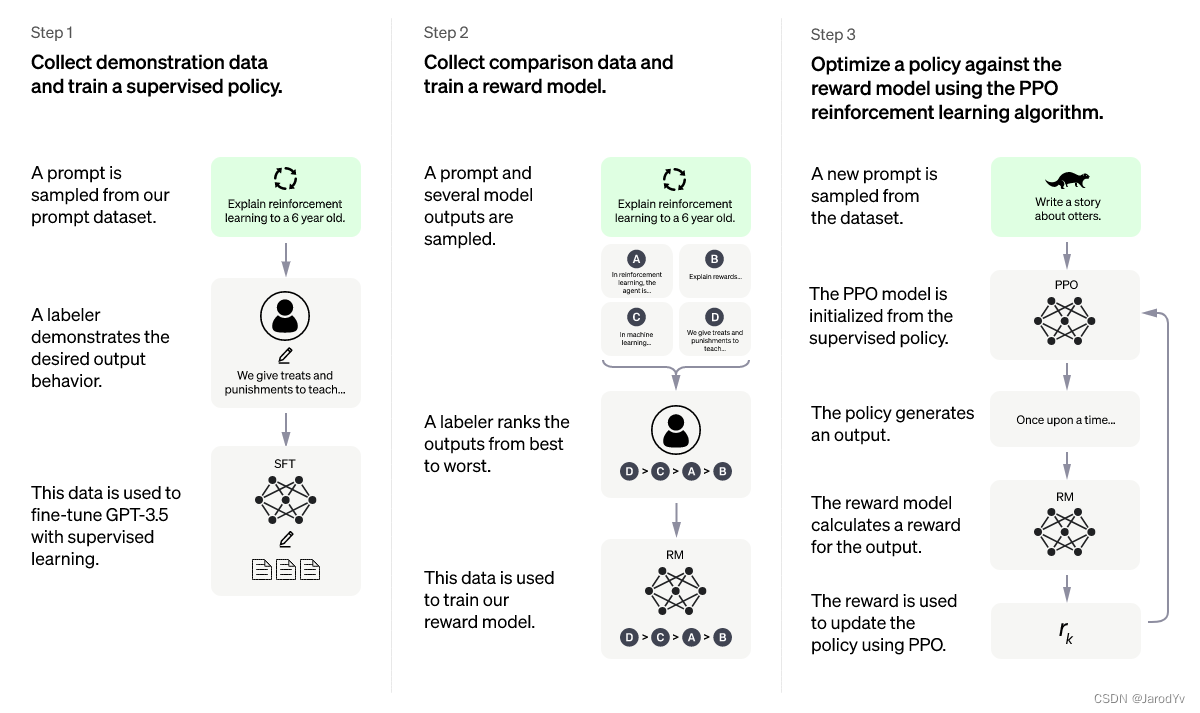
Existem muitos artigos na Internet explicando o algoritmo ChatGPT e o processo de treinamento, mas poucas pessoas explicam o algoritmo de otimização de estratégia proximal em profundidade. Neste artigo, vou me concentrar em explicar o algoritmo de otimização de estratégia proximal e implementá-lo do zero com o PyTorch.

aprendizagem por reforço

Como um algoritmo avançado de aprendizado por reforço, a otimização da estratégia proximal requer uma compreensão do aprendizado por reforço. Existem muitos artigos sobre aprendizado por reforço. Não vou introduzir muito aqui, mas aqui podemos ver como o ChatGPT explica:

A explicação dada pelo ChatGPT é relativamente fácil de entender. Mais academicamente falando, o processo de aprendizado por reforço é o seguinte:

Estrutura de aprendizado por reforço

Na figura acima, o ambiente realimenta recompensas para o agente a cada momento e monitora o estado atual. Com esta informação, o agente realiza ações no ambiente, e então novas recompensas, estados, etc. são realimentados para o agente, formando um loop. Esta estrutura é muito geral e pode ser aplicada em vários campos.

Nosso objetivo é criar um agente que maximize as recompensas. Normalmente, essa recompensa de maximização é a soma das recompensas de desconto de tempo individuais.
$$G=\sum _{t=0}{c}^t{r}_{}$$
Aqui $\gamma$ é um fator de desconto, geralmente na faixa de [0,95, 0,99],$r_{}$é a recompensa no tempo t.

algoritmo

Então, como resolvemos problemas de aprendizado por reforço? Há uma variedade de algoritmos, que podem (para processos de decisão Markov, ou MDPs) cair em duas categorias: baseado em modelo (cria um modelo do ambiente) e livre de modelo (aprende apenas dado um estado).

Classificação de Algoritmos de Aprendizagem por Reforço

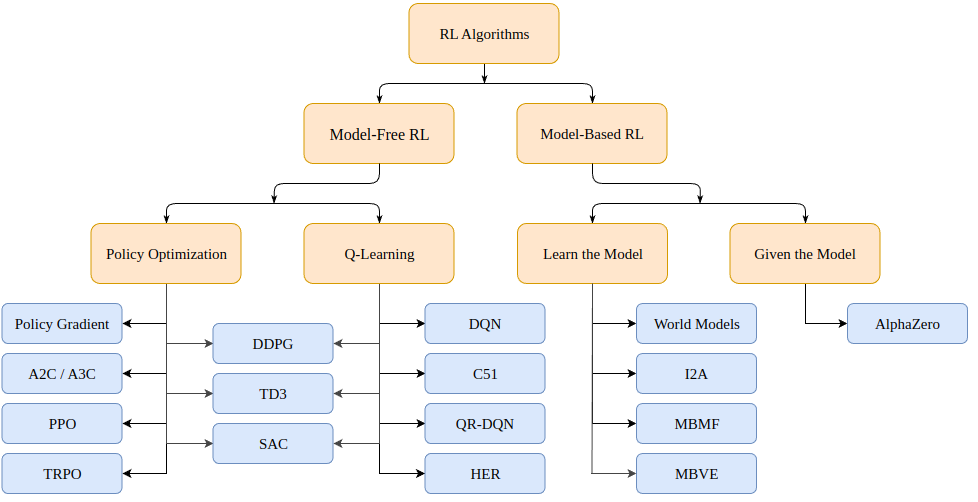
Algoritmos baseados em modelo criam um modelo do ambiente e usam esse modelo para prever estados futuros e recompensas. O modelo é dado (por exemplo, um tabuleiro de xadrez) ou aprendido.

Algoritmos sem modelo aprendem diretamente como agir nos estados encontrados durante o treinamento (otimização de política ou PO) e quais ações de estado geram boas recompensas (Q-Learning).

Os algoritmos de otimização de política proximal que discutimos hoje pertencem à família de algoritmos PO. Portanto, não precisamos de um modelo do ambiente para conduzir o aprendizado. A principal diferença entre os algoritmos PO e Q-Learning é que o algoritmo PO pode ser usado em ambientes com espaços de ação contínua (ou seja, nossas ações têm valores verdadeiros) e pode encontrar a estratégia ideal; e o algoritmo Q-Learning não pode fazer as duas coisas. Esta é outra razão pela qual o algoritmo PO é mais popular. Por outro lado, os algoritmos de Q-Learning tendem a ser mais simples, intuitivos e fáceis de treinar.

Otimização de política (baseada em gradiente)

Os algoritmos de otimização de política podem aprender as políticas diretamente. Para esse propósito, a otimização de políticas pode usar algoritmos sem gradiente, como algoritmos genéticos ou algoritmos baseados em gradiente mais comuns.

Por métodos baseados em gradiente, queremos dizer todos os métodos que tentam estimar o gradiente da política aprendida em relação à recompensa cumulativa. Se conhecermos esse gradiente (ou uma aproximação dele), podemos simplesmente mudar os parâmetros da política na direção do gradiente para maximizar a recompensa.

O método do gradiente de política estima repetidamente o gradiente $g:={\nabla }_{}\mathbb{E}[{\sum }_{t=0}^{}{r}_{}]$ para maximizar a recompensa total esperada. Existem várias expressões relacionadas diferentes para gradiente de política, que são da forma:

$$g=\mathbb{E}\left[\sum _{t=0}{PS}_{}{\nabla }_{}log{\pi }_{}\right({um}_{}|s_{})]\text{\hspace{1em}( 1 )}$$

onde ${PS}_{}$Pode ser o seguinte:

1. ${\sum }_{t=0}^{}{r}_{}$: a recompensa total da trajetória
2. ${\sum }_{t^{\prime }=t}^{}{r}_{t^{}}$: próxima ação $a_{}$recompensa
3. ${\sum }_{t=0}^{}{r}_{}-b\left(s_{}\right)$ : a versão de linha de base da fórmula acima
4. $Q^{\pi }(s_{},a_{})$ : função de valor de ação de estado
5. $A^{\pi }(s_{},a_{})$ : função de vantagem
6. $r_{}+{EM}^{\pi }\left(s_{t+}\right)+{EM}^{\pi }\left(s_{}\right)$ : TD residual

As definições específicas das três fórmulas a seguir são as seguintes:
$$\begin{gathered} {EM}^{\pi }\left(s_{}\right):={\mathbb{E}}_{s_{t+1:},{um}_{t:}}\left[\sum _{l=0}{r}_{t+}\right] \\ {Q}^{\pi }(s_{},a_{}):={\mathbb{E}}_{s_{t+1:},{um}_{t+1:}}\left[\sum _{l=0}{r}_{t+}\right]\text{\hspace{1em}( 2 )} \end{gathered}$$

$$A^{\pi }(s_{},a_{}):=Q^{\pi }(s_{},a_{})-{EM}^{\pi }\left(s_{}\right)\text{\hspace{1em}( 3 )}$$

Observe que existem várias maneiras de estimar gradientes. Aqui, listamos 6 valores diferentes: a recompensa total, a recompensa da ação subsequente, a recompensa menos a versão da linha de base, a função de valor da ação do estado, a função de dominância (usada no artigo original do PPO) e a diferença de tempo ( TD) Diferença residual. Podemos escolher esses valores como nosso objetivo de maximização. Em princípio, ambos fornecem uma estimativa do verdadeiro gradiente que nos interessa.

otimização de estratégia proximal

A otimização de política proximal, ou PPO para abreviar, é um algoritmo (sem modelo) baseado em gradientes de otimização de política. O algoritmo visa aprender uma política que maximize a recompensa cumulativa obtida com base na experiência durante o treinamento.

Consiste em um ator $\pi \theta (.|st)$ e umcrítico (crítico) $V\left(st\right)$ composição. O primeiro no tempo$Gera\; a\; distribuição\; de\; probabilidade\; da\; próxima\; ação\; em\; t$ , que estima a recompensa cumulativa esperada (escalar) para esse estado. Uma vez que tanto os atores quanto os críticos recebem o estado como entrada, a arquitetura do backbone pode ser compartilhada entre as duas redes para extrair recursos de alto nível.

O PPO visa fazer com que a política escolha ações com maior “vantagem”, ou seja, com recompensa cumulativa muito maior do que a prevista pelo avaliador. Ao mesmo tempo, não queremos atualizar muitas estratégias ao mesmo tempo, o que pode causar problemas de otimização. Finalmente, se a política tiver alta entropia, tendemos a dar recompensas extras para incentivar mais exploração.

A função de perda total consiste em três termos: um termo CLIP, um termo de função de valor (VF) e um termo de recompensa de entropia. O objetivo final é o seguinte:
$${eu}_t^{CLIP+VF+}\left(eu\right)={\hat{\mathbb{E}}}_{}\left[L_t^{CLI}\right(eu)-c_{}{eu}_t^V(eu)+c_{}S[{\pi }_{}\left]\right(s_{}\left)\right]$$
onde$c_{}$e $c_{}$são hiperparâmetros que medem a importância da precisão da avaliação da política (crítica) e da exploração (exploração), respectivamente.

item CLIPE

Como dissemos, a função perda motiva a maximização (ou minimização) da probabilidade da ação, que leva à ação vantagem positiva (ou vantagem negativa)
$${eu}^{CLIP}\left(\theta \right)={\hat{\mathbb{E}}}_{}\left[meu\right(r_{}\left(eu\right)A_{},clip\left(r_{}\right(eu),1-ϵ,1+)\_{\hat{A}}_{}\left)\right]$$
Aberto:
$$r_{}\left(eu\right)=\frac{{pi}_{}({um}_{}|s_{}}{{pi}_{{eu}_{ol}}({um}_{}|s_{})}$$
é a proporção que mede a probabilidade de agora (política atualizada) executarmos aquela ação anterior em relação a antes. Em princípio, não queremos que esse coeficiente seja muito grande, porque muito grande significa uma mudança repentina de estratégia. É por isso que tomamos sua soma mínima $[1-ϵ,1+ϵ]$ , onde$\epsilon$ é um hiperparâmetro.

A fórmula de cálculo da vantagem é a seguinte:
$${\hat{A}}_{}=-V\left(s_{}\right)+r_{}+\gamma r_{t+}+c^2{r}_{t+}+\cdots +c^{(T-t+1)}{r}_{T-}+c^{T-t}V\left(s_{}\right)$$
onde:$A_{}$é a vantagem estimada, $-V\left(s_{}\right)$ é o valor estimado do estado inicial,$c^{T-t}V\left(s_{}\right)$ é o valor estimado do estado terminal, e a parte do meio é a recompensa cumulativa observada durante o processo.

Vemos que ele simplesmente mede a resposta do avaliador a um determinado estado $s_{}$grau de erro. Se obtivermos uma recompensa cumulativa maior, a estimativa de probabilidades será positiva e teremos mais chances de agir nesse estado. O inverso também é verdadeiro, se esperarmos uma recompensa maior, mas obtivermos uma recompensa menor, a estimativa de probabilidades será negativa e reduziremos a probabilidade de ação nesta etapa.

Note que se formos até o estado terminal $s_{}$, não precisamos mais confiar no avaliador, podemos simplesmente comparar o avaliador com a recompensa cumulativa real. Nesse caso, a estimativa da vantagem é a vantagem real.

termo de função de valor

Para ter uma boa estimativa da vantagem, precisamos de um avaliador que possa prever o valor de um determinado estado. O modelo é um aprendizado supervisionado com uma perda MSE simples:
$${eu}_t^V=MSE(r_{}+\gamma r_{t+}+\cdots +c^{(T-t+1)}{r}_{T-}+V(s_{}),V(s_{}))=||{\hat{A}}_{}|{|}_{}$$
A cada iteração, também atualizamos o avaliador para que ele nos forneça valores de estado cada vez mais precisos à medida que o treinamento avança.

termo de recompensa de entropia

Por fim, incentivamos uma pequena exploração de recompensa da entropia da distribuição de saída da política. A entropia padrão é:
$$S\left[{\pi }_{}\right]\left(s_{}\right)=-\int {pi}_{}({um}_{}|s_{}\left)log\right(p_{}({um}_{}|s_{}\left)\right){\_}_{}$$

implementação do algoritmo

Se a explicação acima não for clara o suficiente, não se preocupe, o seguinte o levará a implementar passo a passo o algoritmo de otimização de estratégia proximal do zero.

código da ferramenta

Primeiro importe as bibliotecas necessárias

from argparse import ArgumentParser

import gym
import numpy as np
import wandb

import torch
import torch.nn as nn
from torch.optim import Adam
from torch.optim.lr_scheduler import LinearLR
from torch.distributions.categorical import Categorical

import pytorch_lightning as pl

Os hiperparâmetros importantes do PPO são o número de atores, horizonte, epsilon, número de épocas em cada estágio de otimização, taxa de aprendizado, fator de desconto gama e constantes c1 e c2 para pesar diferentes itens de perda. Passamos esses hiperparâmetros por meio de parâmetros.

def parse_args():
    """解析参数"""
    parser = ArgumentParser()

    parser.add_argument("--max_iterations", type=int, help="训练迭代次数", default=100)
    parser.add_argument("--n_actors", type=int, help="actor数量", default=8)
    parser.add_argument("--horizon", type=int, help="每个actor的时间戳数量", default=128)
    parser.add_argument("--epsilon", type=float, help="Epsilon", default=0.1)
    parser.add_argument("--n_epochs", type=int, help="每次迭代的训练轮数", default=3)
    parser.add_argument("--batch_size", type=int, help="Batch size", default=32 * 8)
    parser.add_argument("--lr", type=float, help="学习率", default=2.5 * 1e-4)
    parser.add_argument("--gamma", type=float, help="折扣因子gamma", default=0.99)
    parser.add_argument("--c1", type=float, help="损失函数价值函数的权重", default=1)
    parser.add_argument("--c2", type=float, help="损失函数熵奖励的权重", default=0.01)
    parser.add_argument("--n_test_episodes", type=int, help="Number of episodes to render", default=5)
    parser.add_argument("--seed", type=int, help="随机种子", default=0)

    return vars(parser.parse_args())

Observe que, por padrão, os parâmetros são definidos conforme descrito no artigo. Idealmente, nosso código deve rodar na GPU tanto quanto possível, então precisamos configurar o equipamento da tocha.

def get_device():
    if torch.cuda.is_available():
        device = torch.device("cuda")
        print(f"Found GPU device: {
      
      torch.cuda.get_device_name(device)}")
    else:
        device = torch.device("cpu")
        print("No GPU found: Running on CPU")
    return device

Quando realizamos o aprendizado por reforço, geralmente configuramos um buffer para armazenar o estado, a ação e a recompensa encontrada pelo modelo atual, que é usado para atualizar nosso modelo. Criamos uma função run_timestampsque executará um determinado modelo em um determinado ambiente e obterá um número fixo de timestamps (redefinindo o ambiente se o episódio terminar). Também usamos a opção render=Falsepara que apenas queiramos ver o desempenho do modelo treinado.

@torch.no_grad()
def run_timestamps(env, model, timestamps=128, render=False, device="cpu"):
    """针对给定数量的时间戳在给定环境中运行给定策略。 
    返回具有状态、动作和奖励的缓冲区。"""
    buffer = []
    state = env.reset()[0]

    # 运行时间戳并收集状态、动作、奖励和终止
    for ts in range(timestamps):
        model_input = torch.from_numpy(state).unsqueeze(0).to(device).float()
        action, action_logits, value = model(model_input)
        new_state, reward, terminated, truncated, info = env.step(action.item())

        # (s, a, r, t)渲染到环境或存储到buffer
        if render:
            env.render()
        else:
            buffer.append([model_input, action, action_logits, value, reward, terminated or truncated])

        # 更新当前状态
        state = new_state

        # 如果episode终止或被截断，则重置环境
        if terminated or truncated:
            state = env.reset()[0]

    return buffer

O valor de retorno dessa função (quando não renderizada) é um buffer contendo o estado, as ações executadas, as probabilidades de ação (logits), os valores do avaliador, as recompensas e o estado terminal da política fornecida em cada carimbo de data/hora. Observe que esta função usa um decorator @torch.no_grad(), portanto não precisamos armazenar gradientes para ações realizadas durante a interação com o ambiente.

código principal

Com as funções da ferramenta acima, podemos desenvolver o código central da otimização da estratégia proximal. Primeiro, crie um novo processo de função principal :

def main():
    # 解析参数
    args = parse_args()
    print(args)

    # 设置种子
    pl.seed_everything(args["seed"])

    # 获取设备
    device = get_device()

    # 创建环境
    env_name = "CartPole-v1"
    env = gym.make(env_name)

    # TODO 创建模型，训练模型，输出结果
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
    training_loop(env, model, args)
    model = load_best_model()
    testing_loop(env, model)

O acima é a estrutura do processo do programa geral. Em seguida, só precisamos definir o modelo PPO, treinar e testar as funções.

A arquitetura do modelo PPO não é elaborada aqui, precisamos apenas de dois modelos (ator e crítico) que funcionem no ambiente. Claro, a arquitetura do modelo desempenha um papel crucial em tarefas mais complexas, mas em nossa tarefa simples, um MLP pode fazer o trabalho.

Portanto, podemos criar uma MyPPOclasse . Ao executar o método forward em algum estado, retornamos as ações amostradas do ator, as probabilidades relativas (logits) de cada ação possível e a estimativa do crítico para cada estado.

class MyPPO(nn.Module):
    """
    PPO模型的实现。 
    相同的代码结构即可用于actor，也可用于critic。
    """

    def __init__(self, in_shape, n_actions, hidden_d=100, share_backbone=False):
        # 父类构造函数
        super(MyPPO, self).__init__()

        # 属性
        self.in_shape = in_shape
        self.n_actions = n_actions
        self.hidden_d = hidden_d
        self.share_backbone = share_backbone

        # 共享策略主干和价值函数
        in_dim = np.prod(in_shape)

        def to_features():
            return nn.Sequential(
                nn.Flatten(),
                nn.Linear(in_dim, hidden_d),
                nn.ReLU(),
                nn.Linear(hidden_d, hidden_d),
                nn.ReLU()
            )

        self.backbone = to_features() if self.share_backbone else nn.Identity()

        # State action function
        self.actor = nn.Sequential(
            nn.Identity() if self.share_backbone else to_features(),
            nn.Linear(hidden_d, hidden_d),
            nn.ReLU(),
            nn.Linear(hidden_d, n_actions),
            nn.Softmax(dim=-1)
        )

        # Value function
        self.critic = nn.Sequential(
            nn.Identity() if self.share_backbone else to_features(),
            nn.Linear(hidden_d, hidden_d),
            nn.ReLU(),
            nn.Linear(hidden_d, 1)
        )

    def forward(self, x):
        features = self.backbone(x)
        action = self.actor(features)
        value = self.critic(features)
        return Categorical(action).sample(), action, value

Observe que Categorical(action).sample()uma distribuição categórica é criada com logits de ação e amostras para uma ação (para cada estado).

Finalmente, podemos lidar com o algoritmo real training_loopna função . Como sabemos do papel, a assinatura real da função deve ser assim:

def training_loop(env, model, max_iterations, n_actors, horizon, gamma, 
epsilon, n_epochs, batch_size, lr, c1, c2, device, env_name=""):
  # TODO...

A seguir está o pseudocódigo para o programa de treinamento PPO no papel:

O pseudocódigo do PPO é relativamente simples: simplesmente coletamos as interações com o ambiente por meio de múltiplas cópias do modelo de política (chamadas de atores), e otimizamos as redes de atores e críticos usando objetivos previamente definidos.

Como precisamos medir a recompensa cumulativa que realmente recebemos, precisamos criar uma função que, dado um buffer, substitua a recompensa a cada vez pela recompensa cumulativa:

def compute_cumulative_rewards(buffer, gamma):
    """
    给定一个包含状态、策略操作逻辑、奖励和终止的缓冲区，计算每个时间的累积奖励并将它们代入缓冲区。
    """
    curr_rew = 0.

    # 反向遍历缓冲区
    for i in range(len(buffer) - 1, -1, -1):
        r, t = buffer[i][-2], buffer[i][-1]

        if t:
            curr_rew = 0
        else:
            curr_rew = r + gamma * curr_rew

        buffer[i][-2] = curr_rew

    # 在规范化之前获得平均奖励（用于日志记录和检查点）
    avg_rew = np.mean([buffer[i][-2] for i in range(len(buffer))])

    # 规范化累积奖励
    mean = np.mean([buffer[i][-2] for i in range(len(buffer))])
    std = np.std([buffer[i][-2] for i in range(len(buffer))]) + 1e-6
    for i in range(len(buffer)):
        buffer[i][-2] = (buffer[i][-2] - mean) / std

    return avg_rew

Observe que normalizamos a recompensa cumulativa no final. Este é um truque padrão para tornar os problemas de otimização mais fáceis e o treinamento mais suave.

Agora que temos um buffer contendo o estado, ação tomada, probabilidade de ação e recompensa cumulativa, podemos escrever uma função que, dado o buffer, calcula três termos de perda para nosso objetivo final:

def get_losses(model, batch, epsilon, annealing, device="cpu"):
    """给定模型、给定批次和附加参数返回三个损失项"""
    # 获取旧数据
    n = len(batch)
    states = torch.cat([batch[i][0] for i in range(n)])
    actions = torch.cat([batch[i][1] for i in range(n)]).view(n, 1)
    logits = torch.cat([batch[i][2] for i in range(n)])
    values = torch.cat([batch[i][3] for i in range(n)])
    cumulative_rewards = torch.tensor([batch[i][-2] for i in range(n)]).view(-1, 1).float().to(device)

    # 使用新模型计算预测
    _, new_logits, new_values = model(states)

    # 状态动作函数损失(L_CLIP)
    advantages = cumulative_rewards - values
    margin = epsilon * annealing
    ratios = new_logits.gather(1, actions) / logits.gather(1, actions)

    l_clip = torch.mean(
        torch.min(
            torch.cat(
                (ratios * advantages,
                 torch.clip(ratios, 1 - margin, 1 + margin) * advantages),
                dim=1),
            dim=1
        ).values
    )

    # 价值函数损失(L_VF)
    l_vf = torch.mean((cumulative_rewards - new_values) ** 2)

    # 熵奖励
    entropy_bonus = torch.mean(torch.sum(-new_logits * (torch.log(new_logits + 1e-5)), dim=1))

    return l_clip, l_vf, entropy_bonus

Observe que, na prática, usamos um parâmetro de anelamento que começa em 1 e decai linearmente até 0 ao longo do treinamento. Porque à medida que o treinamento avança, queremos que nossa política mude cada vez menos. Além disso, ao contrário new_logitsde e new_values, não acompanhamos advantageso gradiente da variável, apenas a diferença do tensor.

Agora que temos métodos para interagir com o ambiente e armazenar buffers, calcular a (verdadeira) recompensa cumulativa e obter o termo de perda, podemos começar a escrever o código de treinamento final:

def training_loop(env, model, max_iterations, n_actors, horizon, gamma, epsilon, n_epochs, batch_size, lr,
                  c1, c2, device, env_name=""):
    """使用最多n个时间戳的多个actor在给定环境中训练模型。"""

    # 开始运行新的权重和偏差
    wandb.init(project="Papers Re-implementations",
               entity="peutlefaire",
               name=f"PPO - {
      
      env_name}",
               config={
    
    
                   "env": str(env),
                   "number of actors": n_actors,
                   "horizon": horizon,
                   "gamma": gamma,
                   "epsilon": epsilon,
                   "epochs": n_epochs,
                   "batch size": batch_size,
                   "learning rate": lr,
                   "c1": c1,
                   "c2": c2
               })

    # 训练变量
    max_reward = float("-inf")
    optimizer = Adam(model.parameters(), lr=lr, maximize=True)
    scheduler = LinearLR(optimizer, 1, 0, max_iterations * n_epochs)
    anneals = np.linspace(1, 0, max_iterations)

    # 训练循环
    for iteration in range(max_iterations):
        buffer = []
        annealing = anneals[iteration]

        # 使用当前策略收集所有actor的时间戳
        for actor in range(1, n_actors + 1):
            buffer.extend(run_timestamps(env, model, horizon, False, device))

        # 计算累积奖励并刷新缓冲区
        avg_rew = compute_cumulative_rewards(buffer, gamma)
        np.random.shuffle(buffer)

        # 运行几轮优化
        for epoch in range(n_epochs):
            for batch_idx in range(len(buffer) // batch_size):
                start = batch_size * batch_idx
                end = start + batch_size if start + batch_size < len(buffer) else -1
                batch = buffer[start:end]

                # 归零优化器梯度
                optimizer.zero_grad()

                # 获取损失
                l_clip, l_vf, entropy_bonus = get_losses(model, batch, epsilon, annealing, device)

                # 计算总损失并反向传播
                loss = l_clip - c1 * l_vf + c2 * entropy_bonus
                loss.backward()

                # 优化
                optimizer.step()
            scheduler.step()

        # 记录输出
        curr_loss = loss.item()
        log = f"Iteration {
      
      iteration + 1} / {
      
      max_iterations}: " \
              f"Average Reward: {
      
      avg_rew:.2f}\t" \
              f"Loss: {
      
      curr_loss:.3f} " \
              f"(L_CLIP: {
      
      l_clip.item():.1f} | L_VF: {
      
      l_vf.item():.1f} | L_bonus: {
      
      entropy_bonus.item():.1f})"
        if avg_rew > max_reward:
            torch.save(model.state_dict(), MODEL_PATH)
            max_reward = avg_rew
            log += " --> Stored model with highest average reward"
        print(log)

        # 将信息记录到 W&B
        wandb.log({
    
    
            "loss (total)": curr_loss,
            "loss (clip)": l_clip.item(),
            "loss (vf)": l_vf.item(),
            "loss (entropy bonus)": entropy_bonus.item(),
            "average reward": avg_rew
        })

    # 完成 W&B 会话
    wandb.finish()

Por fim, para ver como ficará o modelo ao final, utilizamos a seguinte testing_loopfunção :

def testing_loop(env, model, n_episodes, device):
    for _ in range(n_episodes):
        run_timestamps(env, model, timestamps=128, render=True, device=device)

Desta forma, nosso programa principal ficará bem simples:

def main():
    # 解析参数
    args = parse_args()
    print(args)

    # 设置种子
    pl.seed_everything(args["seed"])

    # 获取设备
    device = get_device()

    # 创建环境
    env_name = "CartPole-v1"
    env = gym.make(env_name)

    # 创建模型(actor和critic)
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)

    # 训练
    training_loop(env, model, args["max_iterations"], args["n_actors"], args["horizon"], args["gamma"], args["epsilon"],
                  args["n_epochs"], args["batch_size"], args["lr"], args["c1"], args["c2"], device, env_name)

    # 加载最佳模型
    model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
    model.load_state_dict(torch.load(MODEL_PATH, map_location=device))

    # 测试
    env = gym.make(env_name, render_mode="human")
    testing_loop(env, model, args["n_test_episodes"], device)
    env.close()

Isso é tudo acima! Se você entendeu o código acima, parabéns, você entendeu o algoritmo PPO.

para concluir

Proximal Policy Optimization é um algoritmo de otimização de última geração para aprendizado de reforço de política que pode ser usado em praticamente qualquer ambiente. Além disso, a otimização de política proximal tem uma função objetivo relativamente simples e relativamente poucos hiperparâmetros para ajustar.

O ChatGPT depende do PPO para obter mais resultados do que o esperado na terceira etapa. Você pode usá-lo em suas próprias tarefas de aprendizado por reforço e pode obter resultados inesperados.