Estrutura de dados - Árvore de dicas

1. Por que usar a árvore binária de dicas?

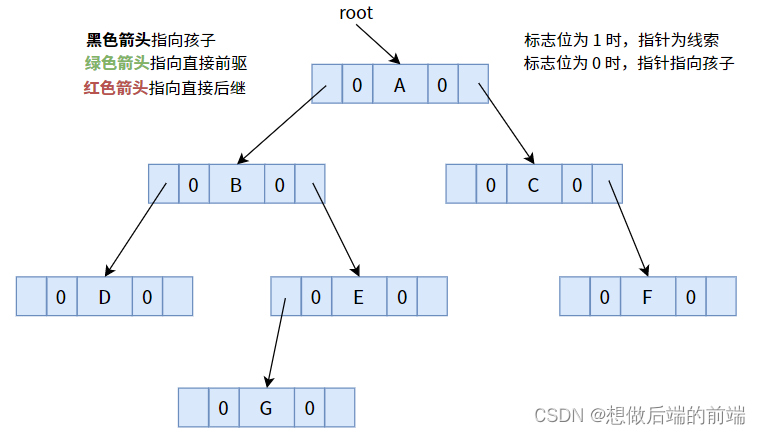
Vejamos primeiro as deficiências das árvores binárias comuns. A seguir está uma árvore binária comum (método de armazenamento encadeado):

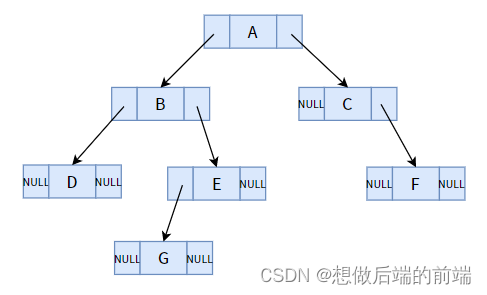
À primeira vista, parece inconsistente? Toda a estrutura possui um total de 7 nós e um total de 14 campos de ponteiro, dos quais 8 campos de ponteiro estão vazios. Para uma árvore binária com n nós, haverá um total de n + 1 campos de ponteiro nulo. Esta regra se aplica a todas as árvores binárias.

Muitos campos de ponteiro nulo não parecem um desperdício? O foco do nosso aprendizado de estruturas de dados e algoritmos é encontrar maneiras de melhorar a eficiência do tempo e a utilização do espaço. Tantos campos de ponteiro são desperdiçados, que desperdício!

Portanto, temos que encontrar maneiras de fazer bom uso deles e usá-los para nos ajudar a usar melhor a estrutura de dados da árvore binária.

Então, como tirar vantagem disso?

A essência de percorrer uma árvore binária é converter os nós da estrutura não linear da árvore binária em uma sequência linear , para que possamos atravessá-la facilmente.

Por exemplo, a sequência de travessia em ordem na figura acima é: DBGEACF.

Para uma sequência linear (tabela linear), possui os conceitos de antecessor direto e sucessor direto. Por exemplo, em uma sequência de travessia em ordem, o antecessor direto de B é D e o sucessor direto é G.

A razão pela qual podemos conhecer o predecessor direto e o sucessor direto de B é porque escrevemos a sequência de percurso em ordem da árvore binária de acordo com o algoritmo de percurso em ordem e, em seguida, usamos essa sequência para dizer de quem é o antecessor e o sucessor. Quem.

O antecessor direto e o sucessor direto não podem ser obtidos diretamente através da árvore binária, pois existe apenas um relacionamento direto entre os nós pais e filhos na árvore binária, ou seja, o campo ponteiro do nó da árvore binária armazena apenas o endereço de seu nó filho.

O requisito atual é que eu queira obter diretamente o predecessor direto e o sucessor direto de um nó no modo de passagem em ordem da árvore binária.

Neste momento, você precisa usar a árvore binária de dicas.

2. O que é uma árvore binária de pistas?

Claro, definitivamente precisamos usar o campo de ponteiro do nó para salvar os endereços do predecessor imediato e do sucessor imediato.

Na verdade, na árvore binária comum da figura acima (a sequência obtida percorrendo em ordem intermediária), alguns nós (nós cujos campos de ponteiro não estão vazios) podem encontrar seus predecessores ou sucessores diretos, como o filho esquerdo G do nó E É o antecessor direto do nó E; o filho direito C do nó A é o sucessor direto do nó A.

Mas isso não funciona para alguns nós (o campo do ponteiro está vazio).Por exemplo, o sucessor direto do nó G é E e o predecessor direto é B. No entanto, tal conclusão não pode ser tirada em uma árvore binária. Como fazer isso? Notamos que os dois campos de ponteiro do nó G são NULL e não foram usados. Portanto, não seria bom se usássemos esses dois ponteiros para apontar para seu antecessor e sucessor, respectivamente?

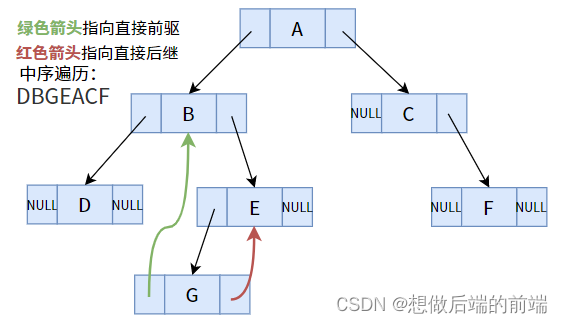
É realmente o melhor dos dois mundos, uma combinação perfeita! Mas o problema não está resolvido!

Como usamos o campo de ponteiro nulo para apontar para o predecessor ou sucessor, isso é contraditório para os nós cujo campo de ponteiro não está vazio, como o nó E e o nó B.

Visto que existe um conflito, devemos descobrir a causa raiz do conflito e resolvê-lo.

A fonte da contradição é: quando o campo do ponteiro do nó está vazio e não vazio, o apontamento do ponteiro é inconsistente. Ou seja, existe uma contradição entre o ponteiro que aponta para o filho quando não está vazio e o antecessor ou sucessor quando o ponteiro está vazio.

Aí tomamos o remédio certo, distinguimos o campo do ponteiro que está vazio e não vazio, e dizemos claramente ao ponteiro: quando não está vazio, aponta para o filho, e quando está vazio, aponta para o antecessor ou sucessor. Isso exige que adicionemos um bit de sinalização a cada um dos dois ponteiros.

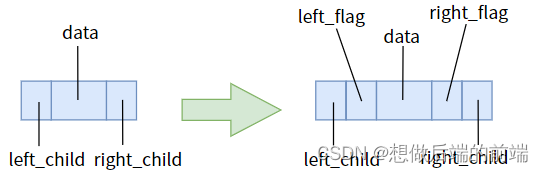
E concorde com as seguintes regras:
Quando left_flag == 0, o ponteiro left_child aponta para o filho esquerdo
. Quando left_flag == 1, o ponteiro left_child aponta para o antecessor imediato.
Quando right_flag == 0, o ponteiro right_child aponta para a direita filho.
Quando right_flag == 1, o ponteiro right_child aponta para o antecessor imediato.

Os nós da árvore binária precisam mudar:

/*线索二叉树的结点的结构体*/
typedef struct Node {
    
    
    char data; //数据域
    struct Node *left_child; //左指针域
    int left_flag; //左指针标志位
    struct Node *right_child; //右指针域
    int right_flag; //右指针标志位
} TTreeNode;

Com a bandeira tudo pode ser resolvido. Chamamos indicadores de pistas para predecessores e sucessores imediatos. Um ponteiro com sinalizador 0 é um ponteiro para um filho, e um ponteiro com sinalizador 1 é uma pista.

Uma árvore de lista vinculada binária tem a estrutura de nós acima. Transformamos todos os ponteiros nulos em pistas. Essa árvore binária é uma árvore de pistas binária.

3. Como criar uma árvore binária de pistas?

Em uma árvore binária comum, se quisermos obter o predecessor ou sucessor direto de um nó em uma determinada ordem de percurso, precisamos percorrer para obter a ordem de percurso todas as vezes antes de podermos conhecê-la. Na árvore binária de dicas, só precisamos percorrê-la uma vez (travessia ao criar a árvore binária de dicas).Depois disso, a árvore binária de dicas pode "lembrar" o predecessor e sucessor direto de cada nó, e não há necessidade de obter através da ordem de passagem no futuro.Precursor ou sucessor.

O processo no qual transformamos uma árvore binária comum em uma árvore binária com pistas de acordo com um determinado método de travessia é chamado de encadeamento de uma árvore binária.

Em seguida, usamos o percurso em ordem para converter a seguinte pista da árvore binária em uma árvore binária de pistas.

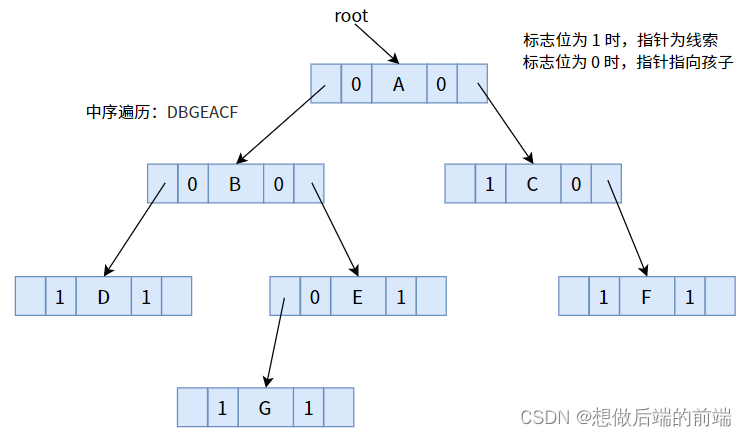
Use o ponteiro com o bit de sinalização 1 para percorrer a sequência em ordem, de modo que aponte para o predecessor ou sucessor:

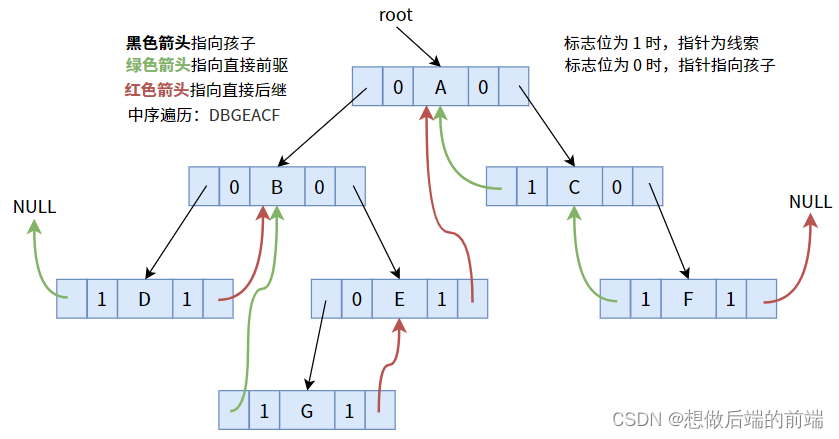
entre eles , o nó D não tem antecessor direto, o nó F não tem sucessor direto, então o ponteiro é NULL.

Neste ponto, resolvemos o desperdício causado por n+1 campos de ponteiro nulo em uma árvore binária com n nós. A solução é adicionar um bit de flag ao ponteiro de cada nó para fazer uso do campo de ponteiro nulo. O bit de sinalização armazena um valor booleano de 0 ou 1, que é relativamente econômico em comparação com o campo de ponteiro nulo desperdiçado. Além disso, a árvore binária tem um novo recurso - os relacionamentos predecessores e sucessores entre os nós em uma determinada ordem de passagem podem ser salvos na árvore binária.

4. Realização de pistas

Observe que a árvore binária de dicas é obtida da árvore binária comum e é obtida em uma determinada ordem de passagem. Porque as pistas só podem ser definidas após conhecer o antecessor e o sucessor de um nó, e o relacionamento entre o antecessor e o sucessor não pode ser refletido diretamente através da árvore binária. O relacionamento só pode ser obtido através da sequência linear obtida ao percorrer a árvore binária. Portanto, após obter a sequência com o relacionamento predecessor e sucessor por meio de algum tipo de método de travessia, o ponteiro nulo do nó pode ser modificado e então a pista pode ser definida.

Ou seja: a essência do threading é o processo de modificar o ponteiro nulo de um nó durante o processo de percorrer uma árvore binária em uma determinada ordem de passagem para que aponte para seu antecessor imediato ou sucessor direto nessa ordem de passagem.

Portanto, a estrutura geral do código ainda é a mesma, só precisamos substituir o código de impressão no código de travessia pelo código encadeado e fazer algumas outras alterações.

A figura a seguir é um exemplo para introduzir três tipos de pistas:

Uma árvore binária não encadeada tem todos os sinalizadores padronizados como 0.

4.1. Threading entre sequências

Após a pista de acordo com a ordem de travessia em ordem, a seguinte figura pode ser obtida:

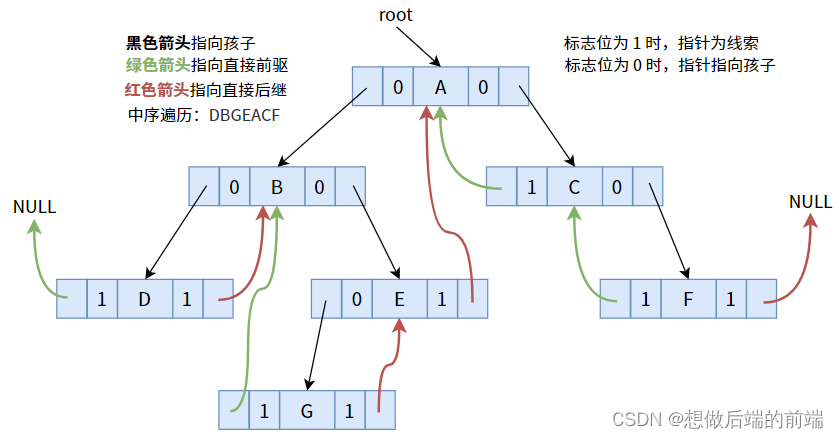
Vamos primeiro esclarecer novamente o seguinte conteúdo:

• Realizamos threading enquanto percorremos a árvore binária.
• A ordem de travessia em ordem é: subárvore esquerda >> raiz >> subárvore direita.
• Threading modifica duas coisas: o campo de ponteiro nulo e seu bit de sinalização correspondente.
• Como modificar? Define o campo de ponteiro nulo para o antecessor ou sucessor imediato.

Então nossa pergunta se torna:

1. Encontre todos os campos de ponteiro nulo.
2. Encontre o nó ao qual pertence o campo do ponteiro nulo, o predecessor direto e o sucessor direto na ordem de pré-ordem.
3. Modifique o conteúdo do campo de ponteiro nulo e seu sinalizador para que o ponteiro seja chamado de pista.

Nota: Usamos recursão ao percorrer a árvore binária, portanto também a usaremos ao encadear.

O código específico é o seguinte:

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;
 
/**
 * 中序线索化
 */
void inorder_threading(TTreeNode *root)
{
    
    
    if (root == NULL) {
    
     //若二叉树为空，做空操作
        return;
    }
    inorder_threading(root->left_child);
    if (root->left_child == NULL) {
    
    
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
    
    
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    inorder_threading(root->right_child);
}

4.2. Threading de pré-encomenda

Após a pista de acordo com a sequência de pré-encomenda, pode-se obter a seguinte imagem:

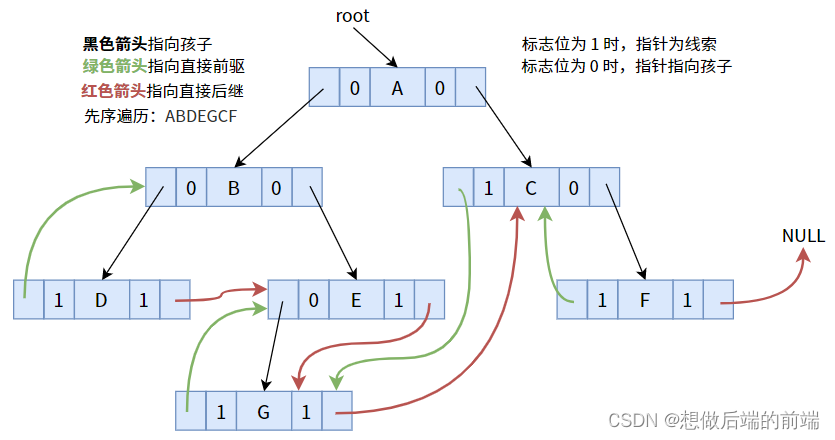
O código específico é o seguinte:

// 全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;
 
/**
 * 先序线索化
 */
void preorder_threading(TTreeNode *root)
{
    
    
    if (root == NULL) {
    
    
        return;
    }
    if (root->left_child == NULL) {
    
    
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
    
    
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    if (root->left_flag == 0) {
    
    
        preorder_threading(root->left_child);
    }
    if (root->right_flag == 0) {
    
    
        preorder_threading(root->right_child);
    }
}

4.3. Threading pós-pedido

Após a pista de acordo com a ordem de travessia pós-ordem, a seguinte figura pode ser obtida:

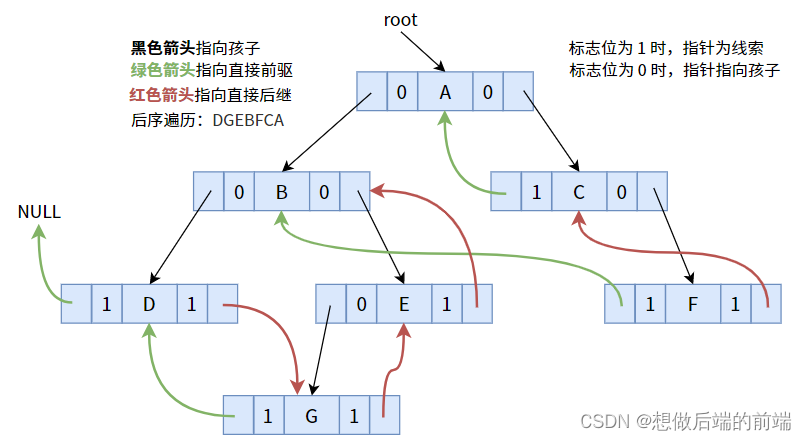
O código específico é o seguinte:

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;
 
/**
 * 后序线索化
 */
void postorder_threading(TTreeNode *root)
{
    
    
    if (root == NULL) {
    
    
        return;
    }
    postorder_threading(root->left_child);
    postorder_threading(root->right_child);
    if (root->left_child == NULL) {
    
    
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
    
    
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
}

5. Resumo

A árvore binária encadeada faz uso total do campo de ponteiro nulo na árvore binária e dá à árvore binária um novo recurso - após passar por uma travessia, os relacionamentos predecessor e sucessor entre seus nós podem ser salvos na árvore binária.

Portanto, se precisarmos percorrer frequentemente a árvore binária para encontrar o nó predecessor ou sucessor direto de um nó, é muito apropriado usar a árvore binária de dicas.