Autor: Yu Fan
fundo
O desenvolvimento da inteligência artificial (IA) introduziu um novo paradigma para a descoberta científica. Hoje, a IA começou a melhorar, acelerar e permitir a nossa compreensão dos fenómenos naturais numa vasta gama de escalas espaciais e temporais, promovendo assim o desenvolvimento das ciências naturais e dando origem ao novo campo de investigação da AI4Science. Recentemente, um artigo de revisão "Inteligência Artificial para Ciência em Sistemas Quânticos, Atomísticos e Contínuos", escrito em conjunto por mais de 60 autores, fornece um resumo técnico aprofundado nos subcampos de sistemas subatômicos, atômicos e contínuos. Aqui extraímos a espinha dorsal técnica desta revisão e nos concentramos em como construir um modelo equivariante sob transformação de simetria.
1. Introdução
Em 1929, o físico quântico Paul Dirac observou: “As leis físicas fundamentais exigidas para a teoria matemática da maior parte da física e de toda a química já são completamente conhecidas por nós, e a dificuldade reside no fato de que a aplicação precisa dessas leis leva a complexo Isso é verdade desde a equação de Schrödinger na física quântica até a equação de Navier-Stokes na mecânica dos fluidos. O aprendizado profundo pode acelerar a solução dessas equações. Usando os resultados dos métodos de simulação tradicionais como dados de treinamento, uma vez treinados, esses modelos podem fazer previsões muito mais rapidamente do que a simulação tradicional.
Noutros campos, como a biologia, os processos biofísicos subjacentes podem não ser totalmente compreendidos e, em última análise, não ser descritos por equações matemáticas. Nestes casos, os modelos de aprendizagem profunda podem ser treinados usando dados gerados experimentalmente, como os modelos de predição de proteínas AlphaFold, RoseTTAFold, ESMFold e outras estruturas 3D obtidas através de experimentos, de modo que a precisão das estruturas 3D de proteínas previstas computacionalmente possa ser comparável aos resultados experimentais .
1.1 Campos científicos
As áreas científicas de interesse deste artigo estão organizadas como uma visão geral na figura abaixo, de acordo com as escalas espaciais e temporais do sistema físico que está sendo modelado.
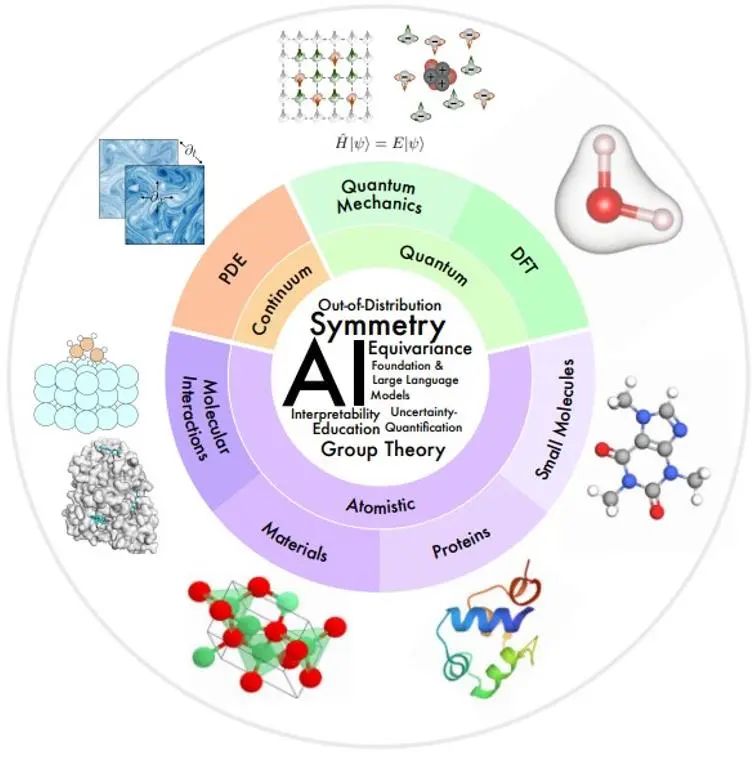
Pequena escala: A mecânica quântica usa a função de onda para estudar fenômenos físicos na menor escala. A equação de Schrödinger que ela obedece descreve o processo dinâmico completo do sistema quântico, mas traz complexidade exponencial. A teoria do funcional da densidade (DFT) e os métodos de química quântica ab initio são métodos de primeiros princípios amplamente utilizados na prática para calcular a estrutura eletrônica e as propriedades físicas de moléculas e materiais, e podem deduzir ainda mais as propriedades eletrônicas e mecânicas de moléculas e sólidos, ópticas. , propriedades magnéticas e catalíticas. No entanto, estes métodos ainda são computacionalmente caros, limitando seu uso a sistemas pequenos (~1000 átomos). O modelo de IA pode ajudar a melhorar a velocidade e a precisão.
Mesoescala: Moléculas pequenas, normalmente com dezenas a centenas de átomos de tamanho, desempenham importantes papéis regulatórios e de sinalização em muitos processos químicos e biológicos. As proteínas são grandes moléculas compostas por uma ou mais cadeias de aminoácidos. A sequência de aminoácidos determina a estrutura da proteína, que por sua vez determina sua função. A pesquisa em ciência de materiais estuda a relação entre processamento, estrutura, propriedades e materiais. As interações moleculares estudam quantas funções físicas e biológicas são realizadas por meio de interações moleculares, como interações ligante-receptor e molécula-material. Nestes campos, a IA fez muitos progressos na caracterização e geração molecular, dinâmica molecular, previsão e design de estruturas de proteínas, previsão de propriedades de materiais e geração de estruturas.
Grande escala: A mecânica contínua usa equações diferenciais parciais para modelar processos físicos que evoluem no tempo e no espaço em nível macroscópico, incluindo fluxo de fluidos, transferência de calor, ondas eletromagnéticas, etc. Os métodos de IA fornecem algumas soluções para problemas como melhoria da eficiência computacional, generalização e análise multi-resolução.
1.2 Campo de tecnologia de IA
Existe um conjunto comum de desafios técnicos em múltiplas áreas da IA científica.
**Simetria:**A simetria é uma paranóia indutiva muito forte, portanto, um desafio importante para a AI4Science é como integrar efetivamente a simetria em modelos de IA.
**Interpretabilidade:**A interpretabilidade é crucial no AI4Science para compreender as leis do mundo físico.
**Generalização e causalidade fora de distribuição (OOD): **Para evitar a geração de dados de treinamento para cada configuração diferente, os fatores causais que permitem a generalização OOD precisam ser identificados.
**Modelos básicos e modelos de linguagem grande:**Os modelos básicos em tarefas de processamento de linguagem natural são pré-treinados sob supervisão autossupervisionada ou generalizável para executar várias tarefas posteriores de maneira rápida ou zero. O artigo fornece uma perspectiva sobre como este paradigma pode acelerar as descobertas da AI4Science.
**Quantificação de Incerteza (UQ): **Estuda como garantir uma tomada de decisão robusta sob incerteza de dados e modelos.
**Educação:** Para facilitar a aprendizagem e a educação, este artigo fornece uma lista categorizada de recursos que o autor considera úteis e fornece perspectivas sobre como a comunidade pode promover melhor a integração da IA com a ciência e a educação.
**2. ** Simetria, equivariância e suas teorias
Em muitos problemas científicos, o objeto de interesse geralmente está localizado no espaço 3D, e qualquer representação matemática do objeto depende de um sistema de coordenadas de referência, tornando tal representação relativa ao sistema de coordenadas. No entanto, os sistemas de coordenadas não existem na natureza, pelo que é necessária uma representação independente do sistema de coordenadas. Portanto, um dos principais desafios da AI4Science é como alcançar a invariância ou equivariância sob a transformação do sistema de coordenadas.
2.1 Visão geral
Simetria refere-se ao fato de que as propriedades de um fenômeno físico permanecem inalteradas sob certas transformações, como transformações de coordenadas. Se existirem certas simetrias no sistema, o alvo de predição é naturalmente invariante ou equivariante sob a transformação de simetria correspondente. Por exemplo, ao prever a energia de uma molécula 3D, o valor previsto permanece inalterado quando a molécula 3D é transladada ou girada. Uma estratégia alternativa para alcançar a aprendizagem consciente da simetria é usar o aumento de dados na aprendizagem supervisionada, aplicando especificamente transformações aleatórias de simetria aos dados de entrada e rótulos para forçar o modelo a produzir previsões aproximadamente equivariantes. Mas isso tem muitas desvantagens:
1) Tendo em conta os graus de liberdade adicionais na selecção do sistema de coordenadas, o modelo requer maior capacidade para representar padrões que são originalmente simples num sistema de coordenadas fixo;
2) Muitas transformações de simetria, como a tradução, podem produzir um número infinito de amostras equivariantes, dificultando que o aprimoramento limitado dos dados reflita totalmente a simetria nos dados;
3) Em alguns casos, é necessário construir um modelo muito profundo para obter bons resultados de previsão. Se cada camada do modelo não conseguir manter a equivariância, será difícil prever o resultado geral da equivariância;
4) Em problemas científicos como a modelagem molecular, é crucial fornecer uma previsão que seja robusta sob transformações de simetria para que o aprendizado de máquina possa ser usado de maneira confiável.
Devido às muitas deficiências do aumento de dados, cada vez mais pesquisas se concentram no projeto de modelos de aprendizado de máquina que atendam aos requisitos de simetria. Sob a arquitetura de adaptação de simetria, o modelo pode se concentrar na tarefa de previsão do alvo de aprendizagem sem aprimoramento de dados.
2.2 Equivariabilidade sob transformação de simetria discreta
Nesta seção, o autor fornece um exemplo de manutenção da equivariância sob transformações discretas de simetria em um modelo de IA. Este problema de exemplo simula o mapeamento de um campo de fluxo escalar em um plano 2D de um momento para o outro. Quando o campo de fluxo de entrada gira 90, 180 e 270 graus, o campo de fluxo de saída também gira de acordo. Sua expressão matemática é a seguinte:
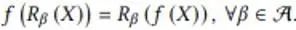
onde f representa a função de mapeamento do campo de fluxo e R representa a transformação de rotação discreta. Cohen et al. propuseram redes neurais convolucionais de grupo equivariante (G-CNNs) para resolver este problema. Seu componente básico mais simples é a convolução ascendente:
1) Primeiro gire o kernel de convolução em todos os ângulos na transformação simétrica e use o kernel de convolução girado para realizar operações de convolução correspondentes na entrada para obter múltiplas camadas de recursos e empilhar essas camadas de recursos na dimensão de rotação recém-gerada α Juntos 2; ) O agrupamento é realizado nesta dimensão de rotação α, de modo que a saída resultante produzirá uma rotação correspondente quando a entrada X for girada.
Devido à existência da operação de pooling, embora as linhas equivariantes sejam mantidas, esses recursos não podem transportar informações de direção. Normalmente, os G-CNNs adotam a estrutura mostrada na figura a seguir:
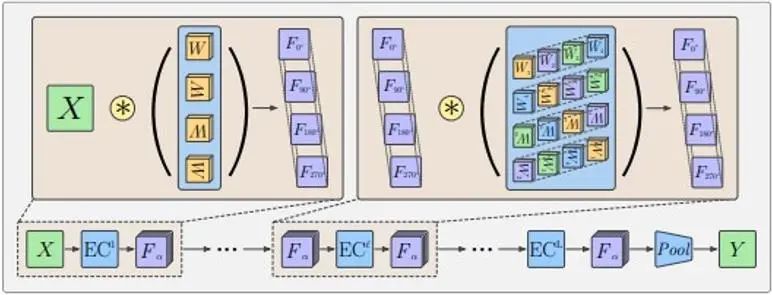
Primeiro, um kernel de convolução rotacional é usado para aumentar a dimensão da entrada, depois uma camada de convolução de grupo multicamadas é usada para fazer com que cada camada de recursos atenda aos requisitos de equivariância rotacional enquanto mantém a dimensão rotacional e, finalmente, uma camada de pooling é usado para eliminar a dimensão rotacional. Isso permite que a camada de feição intermediária detecte melhor padrões em posições relativas e orientações de feições. O significado da equivariância da camada de feição intermediária é que a camada de feição gira de acordo com a transformação de rotação, e a ordem na dimensão de rotação também gira e o design de rotação e rotação do núcleo de convolução na camada de convolução de grupo usada também faz; a saída A camada de feição pode manter essa característica de equivalência.
2.3-2.5 Construção de modelo equivariante de transformação contínua 3D
Em muitos problemas científicos, nos concentramos na rotação contínua e nas simetrias de translação no espaço 3D. Por exemplo, quando a estrutura das moléculas químicas gira e se traduz, o vetor composto de atributos moleculares previstos sofrerá transformações correspondentes. Essas transformações de rotação contínua R e transformações de translação t constituem os elementos do grupo SE(3), e essas transformações podem ser expressas como matrizes de transformação no espaço vetorial. As matrizes de transformação em diferentes espaços vetoriais podem ser diferentes, mas esses espaços vetoriais podem ser decompostos em espaços subvetoriais independentes. Existem as mesmas regras de transformação em cada subespaço, ou seja, o vetor obtido pela aplicação de todos os elementos de transformação do grupo ao vetor do subespaço ainda está no subespaço. Portanto, os elementos de transformação do grupo podem ser irredutíveis no. representação da matriz de transformação. Por exemplo, escalares como energia total e gap de energia permanecem inalterados sob a ação dos elementos do grupo SE(3), e sua matriz de transformação é expressa como D^0(R)=1; Vetores 3D, como campos de força A rotação correspondente ocorre sob a ação, e sua matriz de transformação é expressa como D^1(R)=R em um espaço vetorial de dimensão superior, D^l(R) é um 2l+1; matriz quadrada multidimensional. Essas matrizes de transformação D ^ l (R) são chamadas de matriz Wigner-D de ordem l correspondente à rotação R, e o espaço subvetorial correspondente torna-se o subespaço invariante irredutível de ordem l do grupo SE (3), e o vetor nele é chamado l Vetor equivalente de ordem. Na transformação de translação, esses vetores sempre permanecem inalterados, porque as propriedades que nos interessam estão relacionadas apenas a posições relativas.
A maneira usual de mapear informações geométricas 3D para feições no subespaço invariante do grupo SE(3) é usar o mapeamento de função harmônica esférica. A função harmônica esférica Y^l mapeia um vetor tridimensional em um vetor 2l+1 dimensional, que representa o coeficiente quando o vetor de entrada é decomposto em 2l+1 funções harmônicas esféricas básicas. Conforme mostrado na figura abaixo, como apenas um número limitado de bases é utilizado, a função delta na esfera representada pelo vetor tridimensional será ampliada até certo ponto.

Os harmônicos esféricos têm as seguintes propriedades equivariantes:
Entre eles, D é a matriz Wigner-D de ordem l mencionada anteriormente. Portanto, uma função espacial é decomposta em uma combinação de vetores equivariantes de diferentes ordens sob transformação de rotação.
Supondo que em uma rede neural gráfica com coordenadas atômicas como nós, o recurso do nó h é um vetor equivariante de ordem l_1, então a seguinte transferência e atualização de informações gráficas pode garantir que o h atualizado também mantenha a equivariância:
A etapa principal nisso é a operação do produto tensorial (TP) durante a transferência de informações. Entre eles, vec significa vetorizar a matriz, e o coeficiente C é uma matriz com 2l_3+1 linhas (2l_1+1) (2l_2+1) colunas.
A característica do nó h é um vetor no subespaço invariante irredutível de ordem l_1. A função harmônica esférica Y da direção da borda r_ij é um vetor no subespaço invariante irredutível de ordem l_2. o espaço é redutível, e o coeficiente C é a relação de conversão deste espaço redutível para um subespaço invariante irredutível de ordem l_3. Por exemplo, o espaço do produto direto de dois vetores tridimensionais é o seguinte:
A matriz de transformação de rotação do espaço de produto direto pode ser convertida na matriz diagonal de três blocos no meio da figura acima, o que significa que este espaço pode ser decomposto em três subespaços invariantes irredutíveis com dimensões de 1, 3 e 5, isto é, 3⨂ Decomposição do espaço vetorial de 3=1⊕3⊕5. O coeficiente C é a matriz de transformação deste espaço de nove dimensões para esses espaços unidimensionais, tridimensionais e pentadimensionais, respectivamente. Na fórmula acima, l_1, l_2 e l_3 assumem apenas um valor e são recursos equivalentes de ordem fixa. Os recursos na rede real podem ser uma combinação desses recursos de ordem diferente.
2.6-2.7 Nos exemplos anteriores, foram utilizadas a teoria da teoria dos grupos e as propriedades das funções harmônicas esféricas. Os conhecimentos básicos da teoria dos grupos e das funções harmônicas esféricas são apresentados em detalhes nestes dois capítulos do artigo.
2.8 O kernel dirigível constitui uma forma geral de rede equivariante
As camadas de rede equivariantes anteriores sob transformações discretas e contínuas podem ser descritas na forma de uma convolução variável unificada (CNN direcionável):
Entre eles, xey são coordenadas espaciais, f_in(y) representa o vetor de recursos de entrada na coordenada y, f_out(x) representa o vetor de recursos de saída na coordenada x e K é a transformação do espaço de recursos de entrada para o recurso de saída espaço. A operação de convolução garante equivariância translacional Para garantir equivariância sob outras transformações espaciais afins, o kernel de convolução K também precisa satisfazer as seguintes restrições de simetria:
Entre eles, g é a transformação no grupo de transformação espacial, e ρ_in e ρ_out representam a representação da transformação nos espaços de características de entrada e saída (ou seja, a matriz de transformação), respectivamente.
Neste ponto, a explicação teórica do artigo sobre simetria e equivariância basicamente chegou ao fim, seguida por uma visão geral separada dos múltiplos campos listados no Capítulo 1.
referências
[1] Ren P, Rao C, Liu Y, et al. PhyCRNet: Rede convolucional recorrente informada pela física para resolver PDEs espaçotemporais [J]. Métodos Computacionais em Mecânica Aplicada e Engenharia, 2022, 389: 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
【1】 Xuan Zhang, Limei Wang, Jacob Helwig, et al. 2023. Inteligência Artificial para Ciência em Sistemas Quânticos, Atomísticos e Contínuos. arXiv: https://arxiv.org/abs/2307.08423
【2】 Taco Cohen e Max Welling. 2016. Redes Convolucionais Equivariantes de Grupo. Na Conferência Internacional sobre Aprendizado de Máquina. PMLR, 48:2990–2999.
【3】 Nathaniel Thomas, Tess Smidt, Steven Kearnes, e outros. 2018. Redes de campo tensorial: redes neurais equivariantes de rotação e translação para nuvens de pontos 3D. arXiv: https://arxiv.org/abs/1802.08219
Maurice Weiler, Mario Geiger, Max Welling e outros. 2018. CNNs 3D orientáveis: aprendendo recursos rotacionalmente equivalentes em dados volumétricos. Em Avanços em Sistemas de Processamento de Informação Neural
Um programador nascido na década de 1990 desenvolveu um software de portabilidade de vídeo e faturou mais de 7 milhões em menos de um ano. O final foi muito punitivo! Google confirmou demissões, envolvendo a "maldição de 35 anos" dos programadores chineses nas equipes Flutter, Dart e . Python Arc Browser para Windows 1.0 em 3 meses oficialmente GA A participação de mercado do Windows 10 atinge 70%, Windows 11 GitHub continua a diminuir a ferramenta de desenvolvimento nativa de IA GitHub Copilot Workspace JAVA. é a única consulta de tipo forte que pode lidar com OLTP + OLAP. Este é o melhor ORM. Nos encontramos tarde demais.