rede neural convolucional
Cada kernel de convolução extrai recursos diferentes . Cada kernel de convolução envolve a entrada para gerar um mapa de recursos. Este mapa de recursos reflete os recursos extraídos pelo kernel de convolução da entrada.
- Extração de kernel de convolução superficial: recursos de pixel subjacentes, como bordas, cores e manchas;
- Extração de kernel de convolução de nível médio: recursos de textura de nível médio, como listras, linhas, formas, etc.;
- Extração de kernel de convolução de alto nível: recursos semânticos de alto nível, como olhos, pneus, texto, etc.
Finalmente, a camada de saída de classificação produz o resultado de classificação mais abstrato.
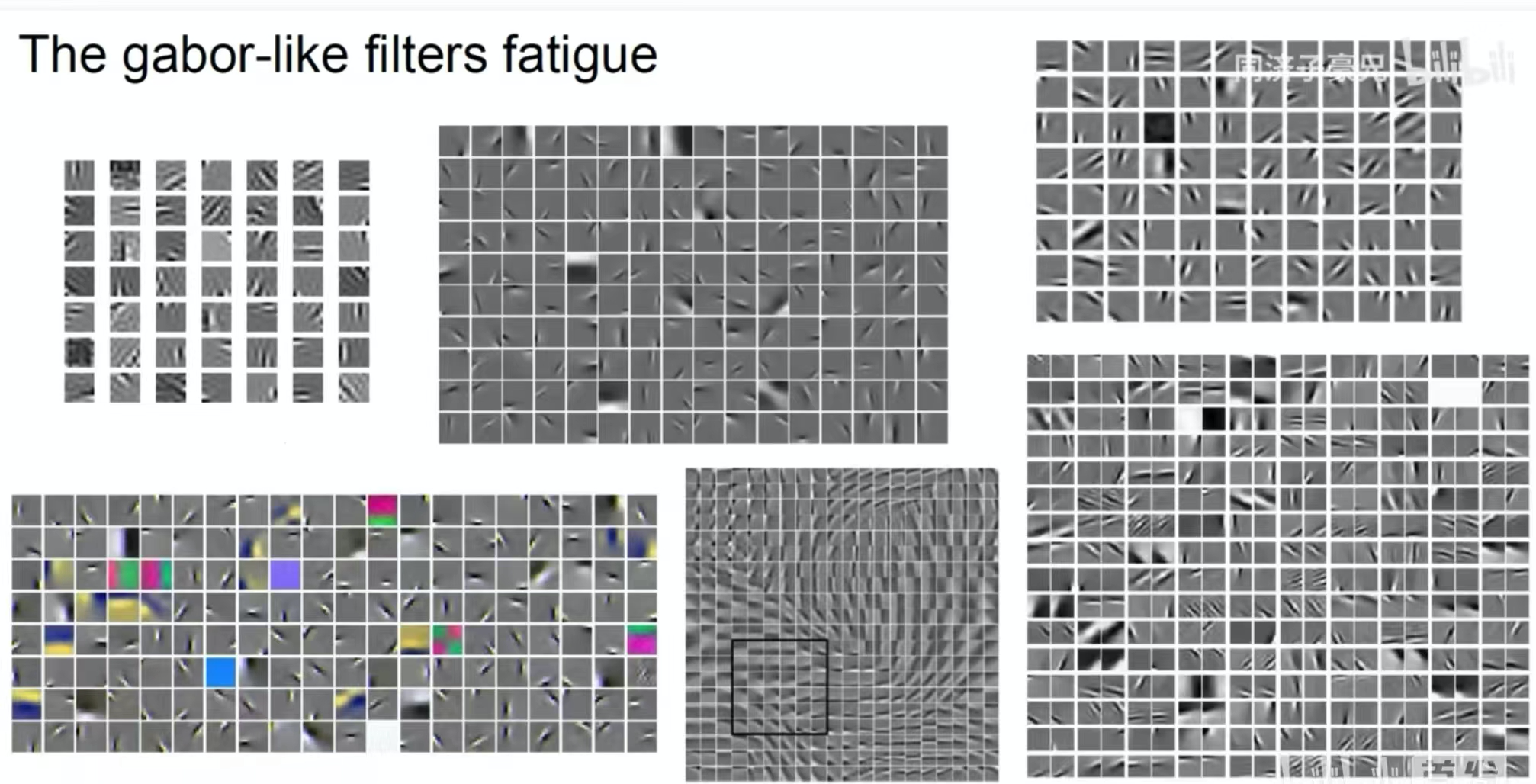
A imagem acima mostra os recursos extraídos por um kernel de convolução raso. Podemos ver que alguns kernels de convolução extraem formas e outros extraem cores. É um recurso de convolução semelhante ao filtro Gabor.

A imagem acima mostra os recursos extraídos pelos kernels de convolução média e profunda. O kernel de convolução média extrai blocos maiores de cor e textura. Os recursos extraídos pelo kernel de convolução profunda podem incluir humanos ou algumas coisas concretas.
Interpretabilidade CAM
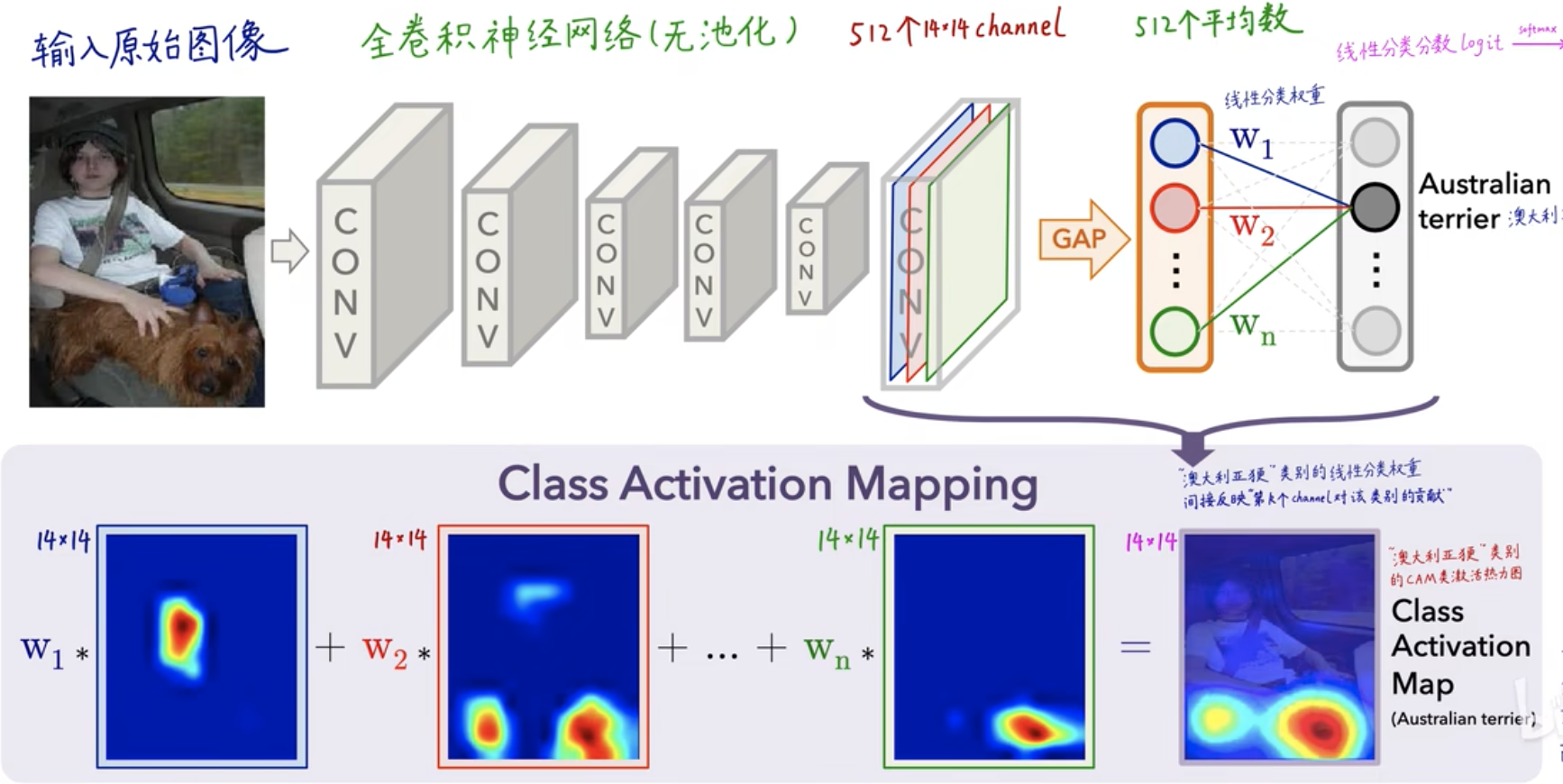
Na figura acima, a imagem original de entrada foi convolvida camada por camada. Na última camada, haverá 512 núcleos de convolução e 512 canais, ou seja, 512 características profundas foram extraídas . Uma média é calculada para cada recurso do canal e, em seguida, o peso (coeficiente) de cada valor do recurso é obtido através da camada FC (camada totalmente conectada) - \(W_1, W_2, W_3,..., W_n\) , para cada categoria Você pode obter um valor de pontuação (pontuação), que é obtido por
\(pontuação=W_1*valor próprio azul+W_2*valor próprio vermelho+...+W_n*valor próprio verde\)
Obtido e, finalmente, calculado um valor de probabilidade por meio de softmax, que é um processo de classificação CNN para mapa de calor CAM, é refletido principalmente no peso do valor do recurso \(W_1, W_2, W_3,..., W_n\) .
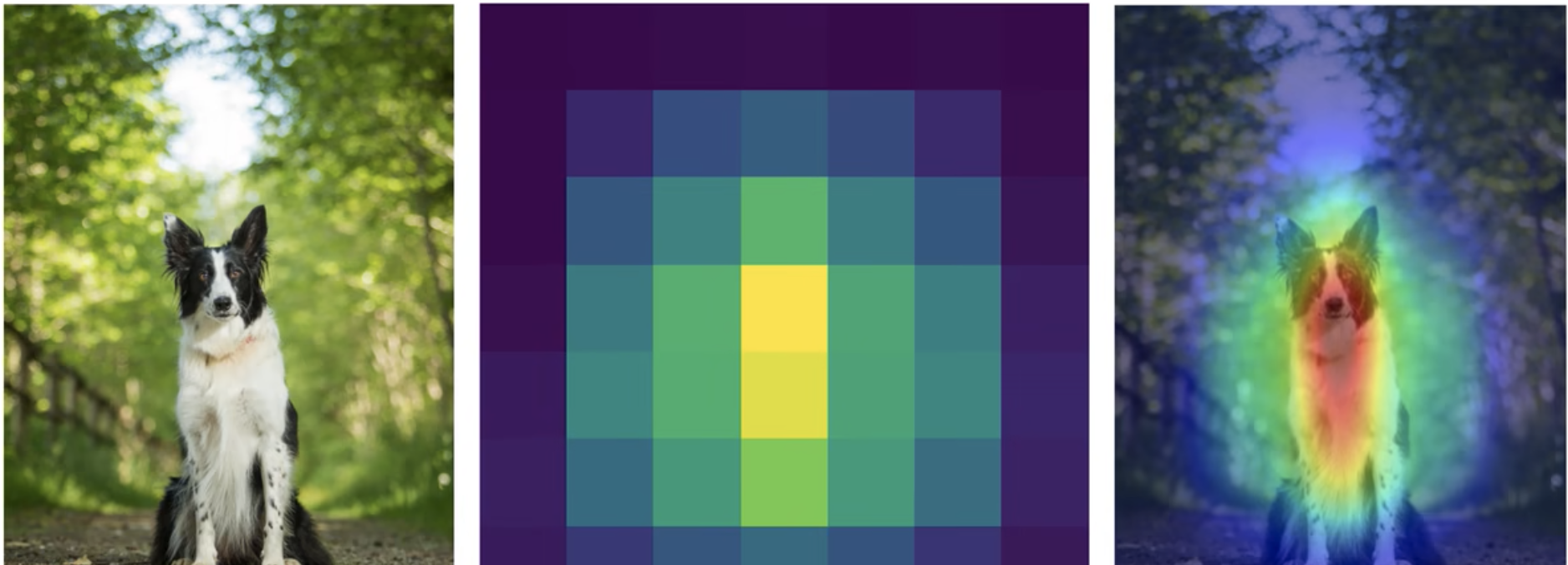
- Desvantagens do CAM
- Deve haver uma camada GAP, caso contrário a estrutura do modelo deverá ser modificada e retreinada.
- Apenas a saída da última camada convolucional pode ser analisada e a camada intermediária não pode ser analisada.
- Apenas tarefas de classificação de imagens
GradCAM

No GradCAM, em vez de usar a camada GAP, você pode usar completamente a camada FC para gerar a pontuação através da camada totalmente conectada, representada por \(y^c\) .
- Derivada de uma matriz
1. A derivada de uma função escalar em relação a um vetor:
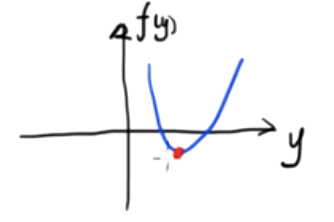
Esta é uma função escalar bidimensional. Sabemos que o valor mínimo desta função é.
\({df(y)\sobre dy}=0\)
Se esta função for uma função escalar tridimensional composta por duas variáveis independentes, a imagem será a seguinte
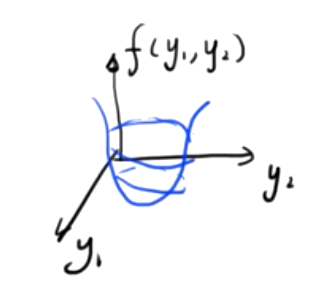
Encontre o valor mínimo desta função binária, simultaneamente
- \({∂f(y_1,y_2)\sobre ∂y_1}=0\)
- \({∂f(y_1,y_2)\sobre ∂y_2}=0\)
Se uma função escalar tem n variáveis independentes \(f(y_1,y_2,y_3,...,y_n)\) , definimos um vetor
S=[ ![]() ]
]
Então a derivada parcial da função em relação ao vetor Y pode ser definida como
\({∂f(Y)\sobre ∂Y}=\) \([\) 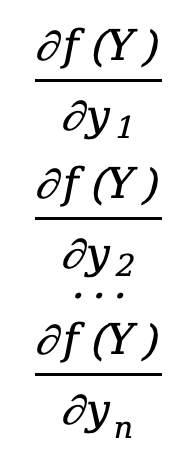 \(]\)
\(]\)
Este é um vetor de coluna n*1 e descobrimos que seu número de linhas é igual ao denominador Y. Esse layout é chamado de layout do denominador .
Da mesma forma, também podemos definir a derivada parcial da função em relação ao vetor Y como
\({∂f(Y)\sobre ∂Y}=[{∂f(Y)\sobre ∂y_1}{∂f(Y)\sobre ∂y_2}...{∂f(Y)\sobre ∂y_n }]\)
Este é um vetor de linha 1*n e descobrimos que seu número de linhas é igual ao numerador f(Y) (um escalar 1*1). Esse layout é chamado de layout de numerador .
O layout do denominador e o layout do numerador são transpostos um do outro .
Exemplo 1: \(f(y_1,y_2)=y_1^2+y_2^2\)
Layout do denominador:
Seja Y=[ ![]() ]
]
mas
\({∂f(Y)\sobre ∂Y}=\) [ ![]() ]=[
]=[ ![]() ]
]
Disposição molecular:
令\(Y=[y_1 y_2]\)
mas
\({∂f(Y)\sobre ∂Y}=[{∂f(Y)\sobre ∂y_1} {∂f(Y)\sobre ∂y_2}]=[2y_1 2y_2]\)
2. Derivada da função vetorial em relação ao vetor
Se nossa função também for um vetor
F(S)=[ 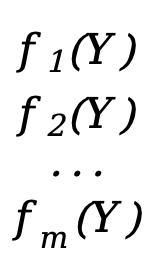 ]
]
Cada \(f_x(Y)\) (x=1,2,3,...,m) aqui é equivalente a uma função escalar f(Y) acima (a variável independente é o vetor Y), F(Y ) é uma função vetorial de m*1.
Exemplo um:
- S=[
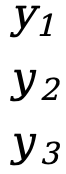 ]
] - F(S)=[
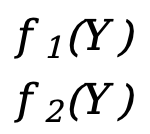 ]=[
]=[ 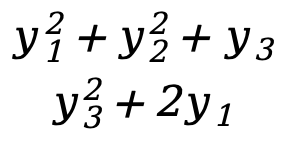 ]
]
A derivada parcial de uma função vetorial em relação a um vetor, o layout do denominador é
\({∂F(Y)\sobre ∂Y}=\) [ 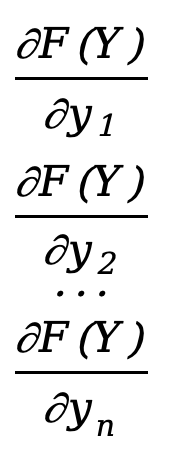 ]=[
]=[ 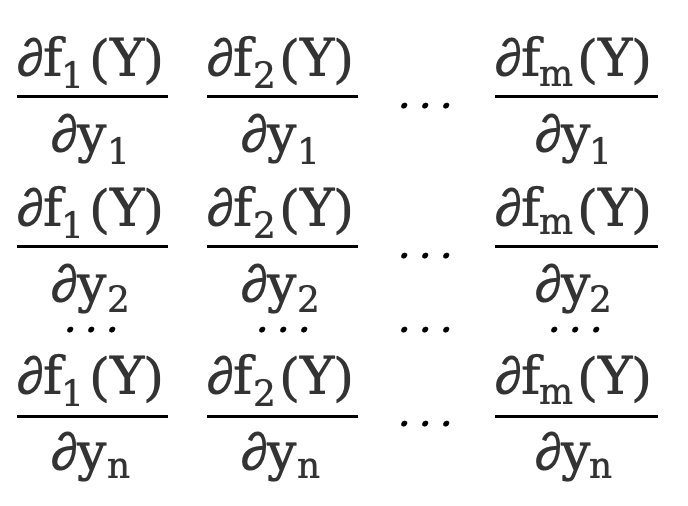 ]
]
Como no Exemplo 1, existem
\({∂F(Y)\sobre ∂Y}=\) [ ![]() ]=[
]=[ 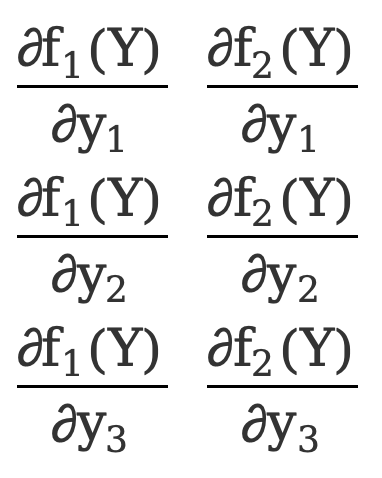 ]=[
]=[ 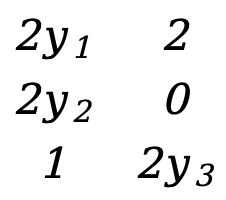 ]
]
Esta é uma matriz 3*2.
Um programador nascido na década de 1990 desenvolveu um software de portabilidade de vídeo e faturou mais de 7 milhões em menos de um ano. O final foi muito punitivo! Google confirmou demissões, envolvendo a "maldição de 35 anos" dos programadores chineses nas equipes Flutter, Dart e . Python Arc Browser para Windows 1.0 em 3 meses oficialmente GA A participação de mercado do Windows 10 atinge 70%, Windows 11 GitHub continua a diminuir a ferramenta de desenvolvimento nativa de IA GitHub Copilot Workspace JAVA. é a única consulta de tipo forte que pode lidar com OLTP + OLAP. Este é o melhor ORM. Nos encontramos tarde demais.
