凸集、凸函数、凸优化与解的最优化条件

凸集、凸函数、凸优化与解的最优化条件

1 凸集

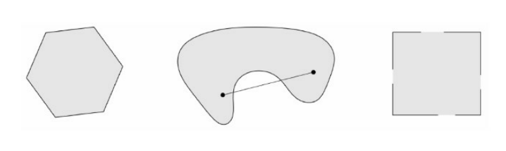
Definition 1.1 A set S is convex if, for any x,y $\in$S and $\theta \in \mathbb{R}$ with 0 $\leq \theta \leq$ 1
$\theta x + (1-\theta)y \in S.$
几何表述：
若集合S中任意两个元素连线上的点也在集合S中，则S为凸集。其示意图如下：

Defination 1.2 设向量{ $x_i$}, i = 1,2,…,n, 如有实数 $\lambda_i \geq 0$, 且 $\sum\limits_{i=1}^{n}{\lambda_i} = 1$, 则称 $\sum\limits_{i = 1}^{n} \lambda_i x_i$为向量{ $x_i$}的一个凸组合（凸线性组合）。

• 性质1: 任意两个凸集的交仍为凸集。
• 性质2: 凸集中任意有限多个点的凸组合仍属于这个凸集。

极点：设S $\subseteq \mathbb{R}^n$是非空凸集，x $\in$S, 若x不能表示为S中两个不同的点的凸组合，则称x是凸集S的极点，即若x = $\alpha x_1 + (1-\alpha)x_2, x_1, x_2 \in S, \alpha \in (0,1)$则必有 $x = x_1 = x_2$.

方向：设S $\subseteq \mathbb{R}^n$是非空凸集，d $\in \mathbb{R}^n 且 d \neq 0$, 若对S中每一个点x都有{x + $\alpha d | \alpha \geq 0$} $\subset$S，则称d为S的方向。

极方向：若S方向d不能表示成两个不同方向的正的线性组合，则称d为凸集S的极方向，即 $d = \lambda_1 d_1 + \lambda_2 d_2, \lambda_1 >0, \lambda > 0 \Rightarrow d_1 = \alpha d_2, \alpha >0$.

2 凸函数

2.1 凸函数定义

Defination 2.1 A function f : $\mathbb{R}^2 \rightarrow \mathbb{R}$ is convex if its domain (denoted $\mathcal{D}$(f)) is a convex set, and if, for all $x_1,x_2$ $\in \mathcal{D}(f)$ and $\theta \in \mathbb{R}, 0 \leq \theta \leq 1$,
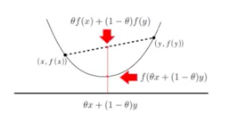
$f(\theta x_1 + (1-\theta)x_2)\leq\theta f(x_1)+(1-\theta)f(x_2).$
Defination 2.2 A function f : $\mathbb{R}^2 \rightarrow \mathbb{R}$ is concave if its domain (denoted $\mathcal{D}$(f)) is a convex set, and if, for all $x_1,x_2$ $\in \mathcal{D}(f)$ and $\theta \in \mathbb{R}, 0 \leq \theta \leq 1$,
$f(\theta x_1 + (1-\theta)x_2)\geq\theta f(x_1)+(1-\theta)f(x_2).$
几何表述：同一位置，x,y 中间点对应函数值一定比两端点对应函数值组合要低。示意图如下：

• 性质1: 若f是凸集S上的凸函数（凹函数），则-f为S上的凹函数（凸函数）。
• 性质2: 若f1，f2时凸集S上的凸函数， $\alpha_1,\alpha_2 \geq 0$，则 $\alpha_1 f_1+\alpha_2 f_2$是S上的凸函数。
• 性质3: 线性函数既是凸函数，也是凹函数。

2.2 凸函数充要条件

凸函数的一阶充要条件为：

S为非空凸集，f为定义在S上的可微函数，则

（1）f是S上的凸函数，当且仅当 $f(y) \geq f(x) + \bigtriangledown f(x)^T(y-x)$.

（2）f是S上的严格凸函数，当且仅当 $f(y) > f(x) + \bigtriangledown f(x)^T(y-x)$.

图像描述：有点类似割线，切线的定义描述。示意图如下：

凸函数的二阶充要条件为：

$\bigtriangledown^2f(x)\succeq0$

补充：若对 $\forall x \in \mathbb{R}^n$， $\bigtriangledown^2 f(x)$是正定的，则f是严格凸函数，但反正不一定。

2.3 正定、半正定、负定矩阵

关于正定、半正定及负定，先有以下补充：

Defination 2.3 给定一个大小为 nxn 的实对称矩阵A，若对于任意长度为n的非零向量x，有 $x^TAx > 0$恒成立，则A是一个正定矩阵。

（单位矩阵是正定矩阵）

Defination 2.4 给定一个大小为 nxn 的实对称矩阵A，若对于任意长度为n的向量x，有 $x^TAx \geq 0$恒成立，则矩阵A是一个半正定矩阵。

（半正定矩阵包括正定矩阵，有点像非负实数和正实数的关系）

那么，如何做题如何具体判断呢？

• 一是求出A的所有特征值。 1）若A的特征值（|A- $\lambda I$|）均是正数，则A是正定的；2）若A的所有特征值均为非负数，则为半正定；3）若A的特征值均为负数，则为负定的。

• 二是计算A的各阶主子式。若A的各阶顺序主子式均大于零，则A是正定的；若A的各阶顺序主子式中奇数阶主子式为负，偶数阶为正，则A是负定的。注意半正定判定时需判定其所有主子式均为非负的才能说明问题，仅仅顺序主子式不可以。

  霍尔维兹定理：

  • 正定：
    $a_{11} > 0,\begin{vmatrix} &a_{11} &a_{12}\\ &a_{21} &a_{22} \end{vmatrix}>0, ···, \begin{vmatrix} a_{11} &··· &a_{1n} \\ ··· &··· &··· \\ a_{n1} &··· &a_{nn} \end{vmatrix}>0$

  • 负定：
    $(-1)^r\begin{vmatrix}a_{11} &··· &a_{1r}\\··· &··· &···\\a_{r1} &··· &a_{rr}\end{vmatrix}>0,(r = 1,2,···,n)$

3 凸优化

Definition 3.1 Armed with the definitions of convex functions and sets, we are now equipped to consider convex optimization problems, Formally, a convex optimization problem is an optimization problem of the form
$minimize \quad f(x)\\subject\: to \quad x\in C$
where f is a concex function, C is a convex set, and x is the optimization variable. However, since this can be a little bit vague, we often write it as
$\begin{aligned}minimize\quad &f(x)\\subject\: to \quad &g_i(x)\leq0, i=1,2,···,k\\&h_j(x) = 0, j=1,2,···，l\end{aligned}$
where f is a convex function, $g_i$ are convex functions, and $h_j$ are affine functions, and x is the optimization variable.

定义说明：

• 类型一：目标函数是凸函数，变量集合为凸集。

• 类型二：目标函数是凸函数，变量约束函数是凸函数（不等式约束），以及affine function ->放射函数（等式约束）。

Theorem： 凸优化问题的局部最优解是全局最优解。（可用反证法proof）

4 解的最优性条件

4.1 无约束最优化问题的最优性条件

考虑以下无约束优化条件：
$\begin{gathered}\underset{x\in\mathbb{R^n}}{min}\,f(x)\end{gathered} \tag{P1}$

• 一阶最优性条件

  Theorem： $f:\mathbb{R^n}\to\mathbb{R}$为定义在 $\mathbb{R}$上的一阶连续可微函数，若 $x^*$是问题的最优解，则 $\bigtriangledown f(x^*)=0$.

  注：该定理为最优解的必要条件，仅使用一阶信息无法判断一个点是否为最优解。

• 二阶最优性条件

  Theorem: $f$同上，若 $x^*$是问题的最优解，则 $\bigtriangledown f(x^*)$, $\bigtriangledown^2f(x^*)$是半正定的。

  补充：若Hesse矩阵为正定的，则 $x^*$是一个严格局部最优解。

无约束凸规划的最优性条件：

$f:\mathbb{R^n}\to\mathbb{R}$是一阶连续可微凸函数，则 $x^*$是f(x)的全局最小值点 $\Leftrightarrow \bigtriangledown f(x^*)=0$

4.2 约束最优化问题的最优性条件

下面考虑一般约束优化问题：
$\begin{aligned}min\quad &f(x)\\s.t.\quad &g_i(x)\geq0, i=1,2,···,k\\&h_j(x) = 0, j=1,2,···，l\end{aligned}\tag{P2}$
其中 $f:\mathbb{R^n}\to\mathbb{R},g_i:\mathbb{R^n}\to\mathbb{R}(i=1,2,···,k),h_j:\mathbb{R}\to\mathbb{R}(j=1,2,···,l)$，故约束集合为：
$\Omega=\{x\in\mathbb{R}|g_i(x)\geq0,i=1,2,···,k;h_j(x)=0,j=1,2,···,l \}$
定义：若 $x^*$是问题(P2)的一个可行解，则不等式约束条件中

（1）有效约束（紧约束，积极约束） $g_i(x^*)=0$

（2）非有效约束（松约束，非积极约束） $g_i(x)>0$

有效约束指标集：
$I(x^*)=\{i|g_i(x^*)=0,i=1,2,···,k\}$
所有有效约束组成的集合：
$A(x^*)=I(x^*)\cup\{j=1,2,···,l\}$
KKT(Karush-Kuhn-Tucker)条件：

一般的，若 $f,g_i,h_j$在 $x^*$处可微，如果 $x^*$是一个最优解， 则应存在常数 $\lambda_1^*, \lambda_2^*, ···, \lambda_k^*, \mu_1^*, \mu_2^*, ···, \mu_l^*$，使得
$\begin{cases}\bigtriangledown f(x^*) = \sum\limits_{i=1}^{k}\lambda_i^*\triangledown g_i(x)+\sum\limits_{j=1}^{l}\mu_j^*\triangledown h_j(x^*)\quad &一阶条件\\g_i(x^*)\geq0,h_j(x^*)=0,i=1,2,···,k;j=1,2,···,l\quad &可行性条件\\\lambda_i^*\geq0, \lambda_i^*g_i(x^*)=0,i=1,2,···,k &互补性条件\end{cases}$
该式称为约束优化条件(P2)的KKT条件。

令 $\lambda^*=(\lambda_i^*), i=1,2,···, k,$，则 $\lambda^* \in \mathbb{R^k}, \mu^* = (\mu_j^*), j=1,2,···, l, \mu^* \in \mathbb{R^l}$，称向量组 $(x^*,\lambda^*,\mu^*)$为约束优化问题（R2）的一个KKT对， $x^*$是约束优化问题（P2）的一个KKT点。

Lagrange函数：
$L(x,\lambda,\mu) = f(x)-\sum\limits_{i=1}^k\lambda_ig_i(x)-\sum\limits_{j=1}^l\mu_jh_j(x)$
其中， $\lambda = (\lambda_1,\lambda_2,···, \lambda_k)^T, \mu = (\mu_1,\mu_2,···,\mu_l)^T$分别是对应不等式约束与等式约束的Lagrange乘子。

5 参考文献

[1] Kolter Z. Convex optimization overview[J]. Convex Optimization Overview, 2008.
链接：https://funglee.github.io/ml/math/3_ConvexOpt.pdf
[2] 机器学习中的凸优化问题
链接：https://blog.csdn.net/chlele0105/article/details/12238839
[3] 正定（positive）与半正定（semi-positive definite）
链接：https://zhuanlan.zhihu.com/p/62589178

写在最后

But the fruit of the Spirit is love, joy, peace, forbearance, kindness, goodness, faithfulness, gentleness and self-control.
To Demut and Dottie!