逻辑斯蒂回归（logistic regression）的梯度下降算法

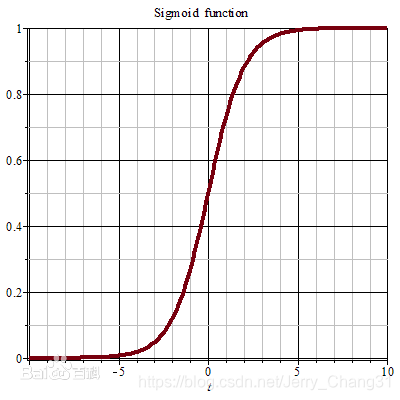
值得注意的是，逻辑回归（logistic regression）解决的是有监督的分类问题，而非回归问题。

分类和回归的区别

分类问题和回归问题的区别在于输出：分类问题的输出是离散型变量，如判断一个人是否得病，只有两种结果：得病或者不得病；而回归问题的输出为连续型变量，如预测一个人五年后的工资，它就可能是一个实数区间内的任意值。

logistic和多重线性回归

实际上，logistic回归和多重线性回归除输出的不同外基本类似，这两种回归可以归于同一个家族，即广义线性模型（generalized linear model）。因此这两个回归的模型形式基本差不多，都可以简单表示为: $y=\Theta^TX$，只是，logistic回归需要借助sigmoid激活函数，将回归问题转化为分类问题。

sigmoid函数

sigmoid激活函数： $g(z)=\frac{1} {(1+e^{(-z)})}$
sigmoid激活函数曲线如下：

由图可以看出，sigmoid函数中z的取值范围为任意实数，g(z)的输出范围为0到1，因此可以将输出看做一个概率值，将回归问题转化为分类问题。
sigmoid函数的一阶导数：
$g'(z)=\frac{1} {(1+e^{-z})^2}*(e^{-z})=\frac{1}{1+e^{-z}}*(\frac{e^{-z}}{1+e^{-z}})=\frac{1}{1+e^{-z}}*(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z))$

logistic回归模型

模型： $h_\theta(x)=g(\Theta x)=\frac{1}{1+e^{-\Theta^{T}x}}$
因此：
$\left\{\begin{matrix} P(y=1|x,\Theta )=h_\theta (x) \\P(y=0|x,\Theta ) =1-h_\theta (x) \end{matrix}\right.$

可将以上两式进行如下组合：
$P(y|x,\Theta)=h_\theta(x)^y(1-h_\theta(x))^{1-y}$

极大似然估计

$L(\Theta)=P(\vec{y}|X,\Theta)=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)},\theta)=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{(y^{(i)})}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}$

两边求对数得：
$logL(\Theta)=\sum_{i=1}^{m}y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))$

求解梯度（求导）

$\frac{\mathrm{d} logL(\Theta )}{\mathrm{d} \theta _j}=(y\frac{1}{h_\theta(x)}-(1-y)\frac{1}{1-h_\theta(x)})\frac{\mathrm{d} }{\mathrm{d} \theta _j}h_\theta(x)$

将 $h_\theta(x)=g(\Theta^Tx)$ 代入上式得：

$\frac{\mathrm{d} logL(\Theta )}{\mathrm{d} \theta _j}=(y\frac{1}{h_\theta(x)}-(1-y)\frac{1}{1-h_\theta(x)})\frac{\mathrm{d} }{\mathrm{d} \theta _j}h_\theta(x)=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})\frac{\mathrm{d} }{\mathrm{d} \theta _j}g(\theta^Tx)$

因为 $g'(z)=g(z)(1-g(z))$，所以上式可化简为：

$\frac{\mathrm{d} logL(\Theta )}{\mathrm{d} \theta _j}=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})g(\theta^Tx)(1-g(\theta^Tx))\frac{\mathrm{d} }{\mathrm{d} \theta _j}\theta^Tx$

$\frac{\mathrm{d} }{\mathrm{d} \theta _j}\theta^Tx=x_j$

所以：

$\frac{\mathrm{d} logL(\Theta )}{\mathrm{d} \theta _j}=\left [ y(1-g(\theta^Tx))-(1-y)g(\theta^Tx) \right ]x_j=\left [ y-yg(\theta^Tx)-g(\theta^Tx)+yg(\theta^Tx) \right ]x_j$

$\frac{\mathrm{d} logL(\Theta )}{\mathrm{d} \theta _j}=(y-g(\theta^Tx))x_j=(y-h_\theta(x))x_j$

梯度下降：

$\theta=\theta-\lambda\Delta$
$\lambda$ 即为学习率
$\Delta$即为梯度

因此对 $\theta_j$ 进行随机梯度下降：
$\theta_j$： $\theta_j-\lambda(g(\theta^Tx^{(i)})-y^{(i)})x_{j}^{(i)}=\theta_j-\lambda(h_\theta(x^{(i)})-y^{(i)})x_{j}^{(i)}$

至此，我们完成了逻辑回归的梯度下降算法的全部推导过程。