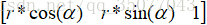《游戏引擎架构》学习笔记（四）

第四章主要是关于学习游戏引擎时所需的一些数学的基础知识。

游戏所需的三维数学

· 在二维中解决三维问题

· 点和矢量

· 点和坐标

· 笛卡尔坐标系

· 圆柱坐标系

· 球坐标系

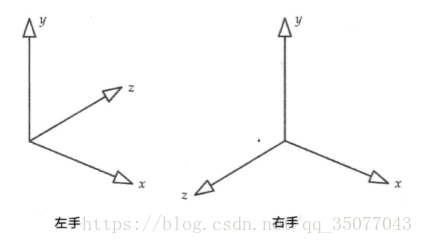
· 左手坐标系与右手坐标系

· 矢量

· 笛卡儿基矢量：三个正交单位矢量i,j,k

· 矢量运算

· 矢量和标量的乘法：缩放

· 非统一缩放：阿达马积

· 加法和减法

· 点和方向的加减

· 模

· 矢量运算的实际应用

· 避免计算平方根

· 归一化和单位矢量

· 法矢量

· 点积和投影

· 矢量投影

· 模作为点积

· 点积判定

· 其他点积的应用

· 测试敌人在玩家的前面或后面

· 计算任一点距平面的高度

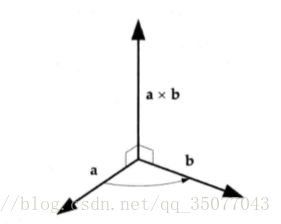
· 叉积

· 叉积的模

· 叉积的方向

· 叉积的特性

· 反交换律

· 分配律

· 叉积的实际应用

· 求垂直于两个矢量的矢量

· 求平面法矢量

· 物理模拟：计算力矩

· 点和矢量的线性插值

· 计算两个点之间的中间点

· 矩阵

· 矩阵乘法

· 以矩阵表示点和矢量

· 采用1*n行矢量乘以n*n矩阵时，矢量必须置于矩阵的左方

· 把n*n矩阵乘以n*1列矢量时，矢量必须置于矩阵的右方

· 单位矩阵

· 逆矩阵

· 矩阵A的逆矩阵能还原矩阵A的变换

· 矩阵串接后求逆，相当于反向串接各个矩阵的逆矩阵

· 转置矩阵

· 计算转置矩阵比计算一般矩阵快

· 对于基于行矢量和列矢量的库，两者的矩阵是转置关系

· 矩阵串接的转置为反向串接各个矩阵的转置

· 齐次坐标

· 变换方向矢量

· 把方向矢量的w设为0

· 基础变换矩阵

· 平移

· 旋转

· 缩放

· 4x3矩阵

· 省略第四列，节省内存

· 坐标空间

· 模型空间

· 世界空间

· 观察空间

· 基的变更

· 坐标空间的层次结构

· 建构改变基的矩阵

· 从矩阵中获取单位基矢量

· 变换坐标系还是矢量

· 变换法矢量

· 法矢量可以使用变换矩阵的逆转置矩阵做变换

· 变换矩阵只含同一缩放无切变时，矩阵可施于任何矢量

· 内存中存储矩阵

· 把矢量连续置于内存

· 分散对齐

· 四元数

· 把单位四元数视为三维旋转

· 矢量qv，标量qs

· q=[qv,qs]

· q=[qx,qy,qz,qw]

· qx=ax*sin(theta/2)

· qy=ay*sin(theta/2)

· qz=az*sin(theta/2)

· qw=cos(theta/2)

· 向量a=[ax,ay,az]是旋转轴方向的单位矢量，theta为旋转角度

· 四元数运算

· 四元数乘法

· pq=[(ps·qv+qs·pv+pv X qv) (ps·qs-pv·qv)]

· 共轭及逆四元数

· 四元数求逆：逆四元数和原四元数的乘积会变成标量1 [0 0 0 1]

· 共轭量 q* = [-qv qs]

· 积的共轭及逆四元数

· (pq)*=q*p*

· (pq)-1=q-1p-1

· 以四元数旋转矢量

· v'=rotate(q,v)=qvq-1=qvq*

· 四元数的串接

· 等价的四元数和矩阵

· 旋转性的线性插值

· 球面线性插值

· SLERP还是不SLERP

· 比较各种旋转表达式

· 欧拉角

· 由三个标量组成：偏航角、俯仰角、滚动角

· 简单，会遭遇万向节死锁

· 3x3矩阵

· 旋转可通过矩阵乘法直接施于点和矢量

· 求逆矩阵来求反转方向的旋转

· 纯旋转的转置矩阵即为逆矩阵

· 不直观，不容易插值

· 轴角

· 以一个矢量定义旋转轴，再加上一个标量定义的旋转角

· 直观，紧凑

· 不能简单插值，旋转不能直接施于点或矢量

· 四元数

· 能串接旋转，并把旋转直接施于点和矢量

· 可以轻易用LERP SLERP进行插值

· 只需存储4个浮点数

· SQT变换

· 包含缩放因子，表示旋转的四元数和平移矢量

· 对偶四元数

· 旋转和自由度

· 其他数学对象

· 直线、光线和线段

· 球体

· 平面

· 轴对齐包围盒

· 定向包围盒

· 平截头体

· 凸多面体区域

· 硬件加速的SIMD运算

· SIMD：单指令多数据

· SSE寄存器

· 每个SSE寄存器包含4个32位float

· 尽量把数据保存在SSE，降低SSE与FPU(浮点运算器)的数据传送

· __m128数据类型

· __m128变量的对齐

· 确保16字节对齐

· 当编译器要动态分配数据结构时，程序员须负责对齐

· 用SSE内部函数编码

· 用SSE实现矢量对矩阵相乘

· 产生随机数

· 线性同余产生器

· 梅森旋转算法

· 所有之母及Xorshift

 

一些个人感觉值得详细记录一下的知识点：

1.左手坐标系和右手坐标系：例如右手坐标系3个轴的方向，可把右手握拳，伸出拇指指向x轴，食指指向y轴，中指指向z轴。

在做3D编程或使用3D软件的时候一定要搞清楚所在的环境是左手坐标系还是右手坐标系

2.矢量的模的计算涉及平方根的计算，而计算平方根在计算机上是费时的运算，应尽量避免。例如，比较两个矢量的相对长度时，可以比较两个矢量的模的平方。因为在笛卡尔坐标系表示的矢量中，矢量的模的平方就是其x,y,z轴方向长度的平方的和（不需要计算平方根）。计算机是怎么计算平方根的呢？查了一下，是通过牛顿迭代法或者泰勒级数的方式不断逼近正确答案，直到误差小于一定的范围为止。

3.叉积的方向：例如右手坐标系下的叉积，可以通过右手法则来表示叉积的方向：伸开右手掌，使除拇指外的4只手指指向矢量a的方向，再把4只手指向内屈指向矢量b的方向，那么拇指的方向便是叉积（a X b）的方向

4.使用矩阵变换方向矢量时，把方向矢量的w值置为0，这样就可以消去平移变换对方向矢量带来的影响。想象一下，如果我们只是对一个模型做平移操作，这个模型的一些向量的信息（比如表面的法向量）肯定是不会改变的。

5.关于旋转矩阵：绕x,y,z轴进行旋转的3个旋转矩阵是这样的：

这是关于在左手坐标系还是右手坐标系下的旋转矩阵呢？绕轴旋转的方向是？

尝试从较简单的情况开始理解：假设有一个行向量表示二维空间上一点

为后续的计算方便写为：

同时有这样一个二维的变换矩阵：

对该点进行矩阵变换：

可以看出这个变换矩阵就是对平面上一点绕原点进行一个逆时针的旋转（一般把逆时针定为正方向），或者说是x至y方向的旋转，再与上面三个轴的旋转矩阵相比，发现这个矩阵与绕z轴旋转的矩阵完全的类似（绕z轴旋转的矩阵只是添加了一个"z坐标不变"的变换）。想象在三维坐标系中，x轴向右，y轴向上，无论这是左手坐标系（z轴向里）还是右手坐标系（z轴向外），这个z轴的旋转矩阵就是绕x至y方向的旋转。

6.关于矩阵旋转：y轴的正负正弦依主轴反射，（即y轴的旋转矩阵的两个正负的正弦值“互换”位置），这个又怎么理解呢？

关于y轴的正负正弦依主轴反射的问题，考虑一个右手坐标系：

想象一下，把坐标系旋转，让三个轴一个指向右，一个向上，一个指向屏幕外；当z轴指向屏幕外，这时的x轴和y轴正好和一般的二维坐标系等同，旋转z轴就正好是对x,y坐标进行二维的旋转变换；把x轴指向屏幕外，坐标系的y轴向右z轴向上，分别对应了二维坐标系的x轴和y轴;而把y轴指向屏幕外，则坐标系的z轴指向了右，x轴指向上。如果y轴的正负正弦不依主轴反射，这里就应该是x轴指向右，z轴指向上了，是不合理的。

7.四元数：关于四元数似乎并没有一个比较好的理解的方式，因为对于四元数的“形象”的理解涉及了“第四维度”，因此可能只能通过数学和公式去理解它了，个人认为，对于四元数，一个应该记一下它的定义

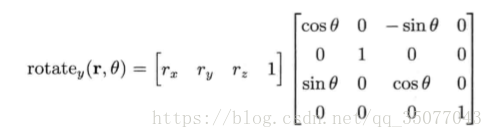
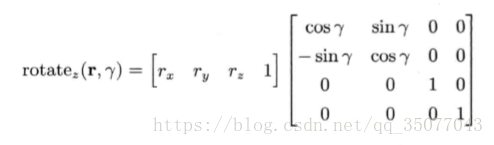
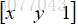
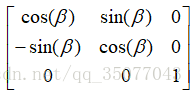
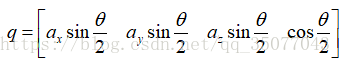其中向量a是旋转轴方向向量， θ是旋转角度，这四个元素本身没有什么特定含义

然后，四元数能串接，能线性插值，能球面线性插值，储存空间小，几乎没什么缺点，游戏引擎中常用来储存旋转变换。记住这些感觉就差不多了。

8.欧拉角的万向节死锁问题：书上只是简单提了下，但这个问题其实并没有想象中那么好理解。要弄懂万向节死锁问题首先要搞明白欧拉角是按特定的顺序进行旋转的，不同的旋转顺序会影响旋转的效果，然后考虑一个简单的例子：右手坐标系下，一架飞机的机身位于xy平面上，头朝y轴方向，然后以z轴,x轴,y轴的旋转顺序对飞机进行“旋转”，同时假设绕x轴旋转的是90度，这时如果旋转z轴，改变的是飞机的偏航角；如果旋转y轴（z轴不旋转的前提下），由于之前绕x轴旋转了90度，此时的飞机已经头朝上（z轴方向）了，此时旋转y轴改变的仍然是飞机的偏航角，于是，就出现了旋转不同的轴却起到相同旋转效果的“bug”。

还存在的问题：

别的都还好，就是四元数那里的太难了，尤其是线性球面插值那些，暂时还不想尝试去理解它。。。