题目背景
小 G 有一群好朋友,他们经常互相借钱。
题目描述
假如说有三个好朋友 A,B,C。A 欠 B \(20\) 元,B 欠 C \(20\) 元,总债务规模为 \(20+20=40\) 元。
小 G 是个追求简约的人,他觉得这样的债务太繁杂了。他认为,上面的债务可以完全等价为 A 欠 C \(20\) 元,B 既不欠别人,别人也不欠他。这样总债务规模就压缩到了 \(20\) 元。
现在给定 \(n\) 个人和 \(m\) 条债务关系,小 G 想找到一种新的债务方案,使得每个人欠钱的总数不变,或被欠钱的总数不变(但是对象可以发生变化),并且使得总债务规模最小。
输入格式
第一行两个数字 \(n\)、\(m\),含义如题目所述。
接下来 \(m\) 行,每行三个数字 \(a_i\)、\(b_i\)、\(c_i\),表示 \(a_i\) 欠 \(b_i\) 的钱数为 \(c_i\)。
注意,数据中关于某两个人 A 和 B 的债务信息可能出现多次,将其累加即可。 如 A 欠 B \(20\) 元、A 欠 B \(30\) 元、B 欠 A \(10\) 元,其等价为 A 欠 B \(40\) 元。
输出格式
输出文件共一行,输出最小的总债务规模。
数据范围
评测时间限制 \(1000\ \textrm{ms}\),空间限制 \(128\ \textrm{MiB}\)。
- 对于 \(30\%\) 的数据,\(1\le n\le 10\),\(1\le m\le 10\);
- 对于 \(60\%\) 的数据,\(1\le n\le 100\),\(1\le m\le 10^4\);
- 对于 \(80\%\) 的数据,\(1\le n\le 10^4\),\(1\le m\le 10^4\);
- 对于 \(100\%\) 的数据,\(1\le n\le 10^6\),\(1\le m\le 10^6\)。
对于所有的数据,保证 \(1\le a_i,b_i\le n\),\(0<c_i\le 100\)。
分析
这道题的数据范围和输出形式,都指向了一个可能的方案,而我们的任务就是去证明。
\(100\ \texttt{pts}\)
我们先来考虑一个比较简单的情况:
- A 欠 B \(1\) 块钱;
- B 欠 A \(1\) 块钱。
这样,我们就能够抵消掉。
这就是这个模型的第一个性质,我们不妨称其为抵消法则。
同样地,如果
- A 欠 B \(1\) 块钱;
- B 欠 C \(1\) 块钱。
则 A 欠 C \(1\) 块钱。这就可以称为继承法则。
这就是这个模型的全部吗?并不是。比如这个情况:
- A 欠 B \(2\) 块钱;
- B 欠 A \(1\) 块钱。
这不是用一个抵消法则能够解决的。我们还要加入一种分裂法则,即 A 欠 B \(2\) 块钱可以变成两个 A 欠 B \(1\) 块钱。
这下子问题似乎变得很复杂,但是我们将一个问题的核心法则抽象出来了,这样就可以自动屏蔽掉很多无关信息。
我们利用这些法则和常识,发现了一个比较有可能是可以的方法:
- 初始每个人都有一个资产值 \(v_i\),赋为 \(0\);
- 每发生一次借债 \(\left<a_i,b_i,c_i\right>\),借债方 \(a_i\) 的资产加上 \(c_i\),还债方 \(b_i\) 的资产减去 \(c_i\);
- 最后的答案就是 \(\large{\sum\limits_{v_i>0}v_i}\) 或 \(\large{\left|\sum\limits_{v_i<0}v_i\right|}\)。
这个方法看似没问题(虽然的确没问题),但是严格的数学证明是不可少的。我们要证明两件事:
- 最优性,即不可能有比这个方案还要小的债务规模。
- 可行性,则必然存在一种借债方案,使得这样的债务规模可以实现。
最优性很好证明。
首先,对于任意的债务方案,最后的「资产」一定不变。这是很好证明的,利用几个法则就能够轻易推出。
则肯定不会存在一种方案,比直接利用最后资产倒推的方案来得好。这就是「最终资产」的不变性决定的。
那么,这一种所谓的方案又应该如何去构造呢?实际上很好解决。
我们可以将欠债(即「资产」为负)的人放在一起,而债主(「资产为正」的)放在一起。
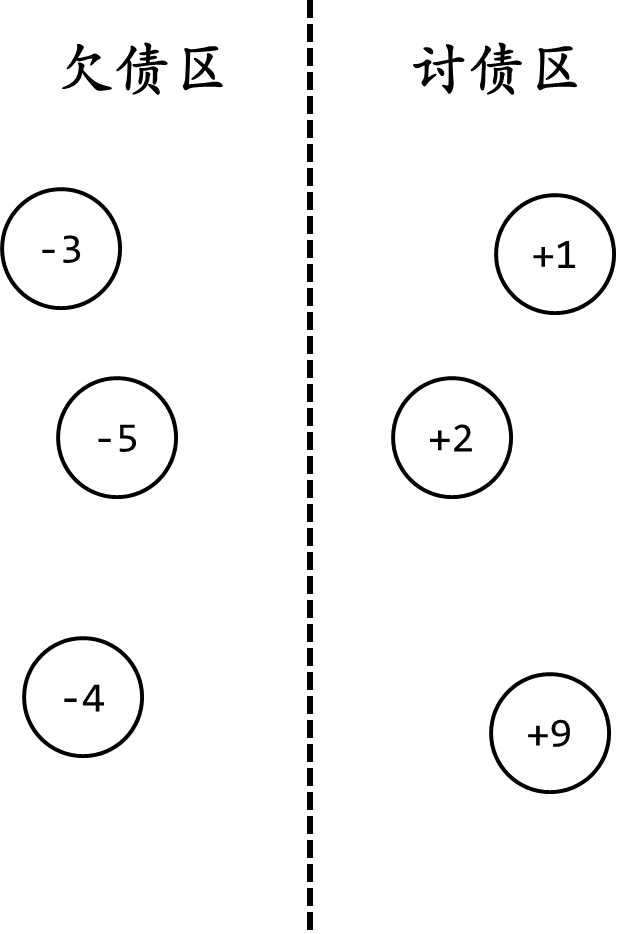
然后我们可以对两边分别列出一个顺序。就像这样:
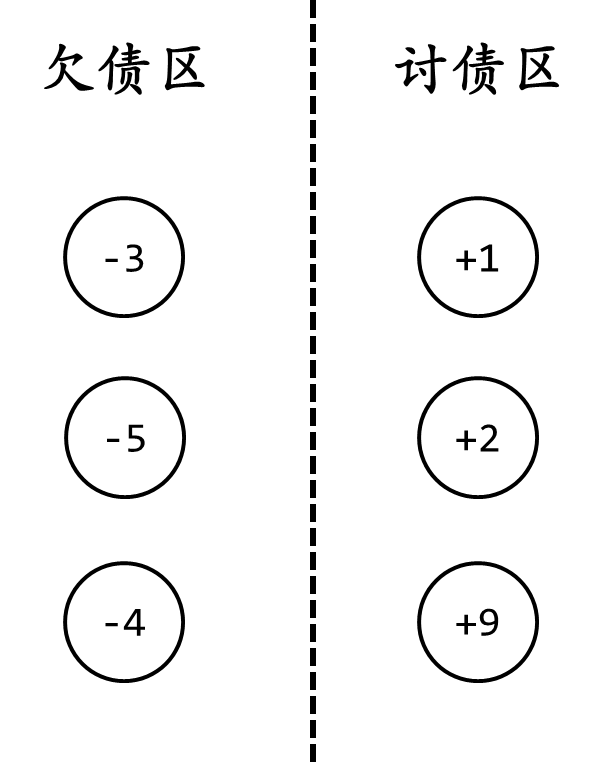
然后,我们将两边的第一个连起来,构造一个债务关系。
比如这个情况,我们就能够在 -3 和 +1 之间建立债务关系。-3 要还 +1 \(1\) 块钱。
此时,+1 心满意足地走了,场地变成这个样子:
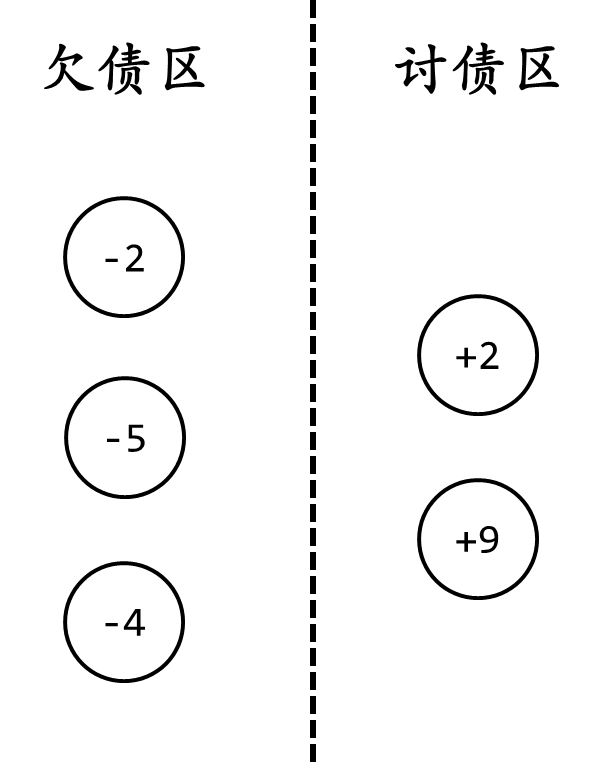
我们只要一直这样,就能不停地缩小债务规模。这样递归求解就能够构造出一个方案,易证这是最优的。
Code
代码十分简单,不用过多注释。
// @author 5ab
#include <cstdio>
#include <cctype>
using namespace std;
const int max_n = 1000000;
int cnt[max_n] = {};
inline int read()
{
int ch = getchar(), n = 0, t = 1;
while (isspace(ch)) { ch = getchar(); }
if (ch == '-') { t = -1, ch = getchar(); }
while (isdigit(ch)) { n = n * 10 + ch - '0', ch = getchar(); }
return n * t;
}
int main()
{
int n = read(), m = read(), ta, tb, tc, ans = 0;
for (int i = 0; i < m; i++)
{
ta = read() - 1, tb = read() - 1, tc = read();
cnt[ta] -= tc;
cnt[tb] += tc;
}
for (int i = 0; i < n; i++)
if (cnt[i] > 0)
ans += cnt[i];
printf("%d\n", ans);
return 0;
}
后记
这道题的关键反而是生活常识。没有生活常识可能会较难作出此题。
所以,OI 也不能过度脱离生活。有时是生活给 OI 灵感,有时是 OI 给生活动力。OI 并不独立于生活。