【学习计算机组成原理】原码的乘运算

无符号数的乘法

和现实联系起来，我们求两个数的乘法时怎么算。
例如，求0.1000乘以0.1110的结果。（两个纯小数）
我们会列一个算式，如下：（只计算小数点往右的数）

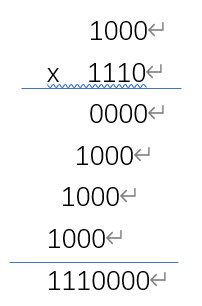
1000是被乘数，1110是乘数。拿乘数的每一位和被乘数相乘，得到的数向左移动相应的位数，最后相加就是结果。
最后相加时，是0+10000+100000+1000000=1110000，然后小数点加在最前方。
如果我们把上面相加的数表示成这样：
$0.0000000=0000\times10^{-4}$
$0.0010000=1000\times10^{-3}$
$0.0100000=1000\times10^{-2}$
$0.1000000=1000\times10^{-1}$
最终相加就是 $0000\times10^{-4}+1000\times10^{-3}+1000\times10^{-2}+1000\times10^{-1}$
这样，乘法的步骤就可以用算式表示，而不是口头描述左移相加。

如果上面的数是二进制数，拿乘数的每一位和被乘数相乘，若乘数的一位是1，1和被乘数相乘还是被乘数，若乘数的一位是0，0和被乘数相乘是0。

一位的值	递推公式
0	$p_{i+1}=2^{-1}\times P_{i}$
1	$p_{i+1}=2^{-1}\times(P_{i}+X)$

$0000000=0000\times2^{-4}$
$0010000=1000\times2^{-3}$
$0100000=1000\times2^{-2}$
$1000000=1000\times2^{-1}$
相应的求和：
$2^{-4}\times0000+2^{-3}\times1000+2^{-2}\times1000+2^{-1}\times1000$
$=2^{-1}\times(1\times1000+2^{-1}\times(1\times1000+2^{-1}\times(1\times1000+2^{-1}\times(0\times1000+0))))$
这样得到一个递推公式：
设被乘数是X，乘数是Y，Y从右往左每一位依次是y₁，y₂…y_n
$P_i=2^{-1}\times(y_{i}\times X+P_{i-1})$   $1\leq i \leq n$
$P_0=0$
所以在机器中运算乘法的过程如下：（因为是无符号数，所以是逻辑右移，高位补0）

• 循环n次，从乘数的最低为y₁开始，到乘数的最高位y_n结束。
• 每次判断y_i的值，值为1，则加被乘数后右移；值为0，则直接右移（加0后右移）
• 循环结束，求得P_n
  例如：求14乘13的结果
  设被乘数是1110，乘数是1101，用C表示进位位，P表示部分的积，R表示乘数。

1. 0 0000 1101最低位是1，乘积P加被乘数1110，再整体右移，得到结果0 0111 0110
2. 0 0111 0110最低为是0，整体右移，得到结果0 0011 1011
3. 0 0011 1011最低位是1，乘积P加被乘数1110，再整体右移，得到结果0 1000 1101
4. 0 1000 1101最低位是1，乘积P加被乘数1110，再整体右移，得到结果0 1011 0110
   
   结果是1011 0110=182

原码乘法

原码用于表示浮点数的尾数部分，所以原码乘法将用于浮点数的乘法过程中。
现实中的数，正负号和数值一般是分开运算的，数值乘完加上符号就是结果，两个数的符号，同号为正，异号为负。
所以，原码有符号位和数值位，做乘法运算时，分开处理，数值位当作无符号数的乘法运算，符号位异或即为结果的符号位。

更高的效率

当数有n位时，需要循环n次，可能有点慢，之前我们每次只判断乘数的一位数，如果判断两位，那么只需要循环n/2次，快了不少。

两位的值	递推公式
00	$p_{i+1}=2^{-2}\times P_{i}$
01	$p_{i+1}=2^{-2}\times(P_{i}+X)$
10	$p_{i+1}=2^{-2}\times(p_{i}+2X)$
11	$p_{i+1}=2^{-2}\times(p_{i}+3X)=2^{-2}\times(p_{i}+4X-X)=2^{-2}\times(p_{i}-X)+X$（加X在左移之后加）

• 使用T触发器判断左移之后是否执行加X
• 减X使用加X的变补实现
• 2X表示X左移一位

三位真值表

yi+1	yi	T	操作	迭代公式
0	0	0	T=0	$p_{i+1}=2^{-2}\times P_{i}$
0	0	1	+X ; T=0	$p_{i+1}=2^{-2}\times(P_{i}+X)$
0	1	0	+X ; T=0	$p_{i+1}=2^{-2}\times(P_{i}+X)$
0	1	1	+2X ; T=0	$p_{i+1}=2^{-2}\times(p_{i}+2X)$
1	0	0	+2X ; T=0	$p_{i+1}=2^{-2}\times(p_{i}+2X)$
1	0	1	+3X ; T=1	$p_{i+1}=2^{-2}\times(p_{i}-X)$
1	1	0	+3X ; T=1	$p_{i+1}=2^{-2}\times(p_{i}-X)$
1	1	1	T=1	$p_{i+1}=2^{-2}\times P_{i}$

比较特殊的是这里的移位是算术右移，避免用减法时，符号出错