题意:
题目中「移动」的意思是:做一次实验,把一个鸡蛋从某个楼层扔下去,看它是否破碎。没有破碎的鸡蛋可以重复使用;
这 K 个鸡蛋,F 值满足的特点是:
在所有小于等于 F 的楼层扔下它不破碎;
在所有大于 F 的楼层扔下它一定会破碎;
所有鸡蛋的 F 值都一样,且确定的,并且 0 <= F <= N,即 F 值一定不会超过楼层高度。
F值是确定的,但它不是题目要我们求的。题目要我们求的是找到这个 F 值的最小实验次数。这其实是时间复杂度的概念,时间复杂度是在最坏情况下(即运气最差的情况下),程序执行完毕最少执行的次数,例如:
在一个数组(长度为 N)里查找一个数,找到某个数可以用线性查找,最好情况下,下标为 0 的位置就是要找的元素,但是在计算复杂度的时候,需要考虑到最差情况,即看到最后一个位置的时候,才找到这个元素,因此至少执行数组长度这么多次的查找,才能找到;
在一个有序数组(长度为 N)里查找,可以使用二分查找算法,最好情况下依然是 1 次就找到(中点位置),但是最坏情况下,例如中点的两个邻居,就得找logN(这个数值需要上取整,这里不深究)次;
第 1 步:定义状态
dp[i][j]:一共有 i 层楼梯(注意:这里 i 不表示高度)的情况下,使用 j 个鸡蛋的最少实验的次数。
说明:
1、i 表示的是楼层的大小,不是高度(第几层)的意思,例如楼层区间 [8, 9, 10] 的大小为 3。
2、j 表示可以使用的鸡蛋的个数,它是约束条件。
第一个维度最先容易想到的是表示楼层的高度,这个定义的调整是在状态转移的过程中完成的。因为如果通过实验知道了鸡蛋的 F 值在高度区间 [8, 9, 10] 里,这个时候只有 1 枚鸡蛋,显然需要做 3 次实验,和区间的大小是相关的。
注意:这里我定义的维度顺序和官方解答的定义是反着的,我个人习惯将约束的那个条件,放置在后面的维度,表示消除后效性的意思。
第 2 步:推导状态转移方程
推导状态转移方程经常做的事情是「分类讨论」,这里「分类讨论」的依据就是,在指定的层数里扔下鸡蛋,根据这个鸡蛋是否破碎,就把问题拆分成了两个子问题。
设指定的楼层为 k,k >= 1 且 k <= i:
如果鸡蛋破碎,测试 F 值的实验就得在 k 层以下做(不包括 k 层),这里已经使用了一个鸡蛋,因此测出 F 值的最少实验次数是:dp[k - 1][j - 1];
如果鸡蛋完好,测试 F 值的实验就得在 k 层以上做(不包括 k 层),这里这个鸡蛋还能使用,因此测出 F 值的最少实验次数是:dp[i - k][j],例如总共 8 层,在第 5 层扔下去没有破碎,则需要在 [6, 7, 8] 层继续做实验,因此区间的大小就是 8 - 5 = 3。
最坏情况下,是这两个子问题的较大者,由于在第 k 层扔下鸡蛋算作一次实验,k 的值在 1≤k≤i,对于每一个 k 都对应了一组值的最大值,取这些 k 下的最小值(最优子结构),因此:
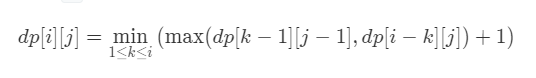
解释:
由于仍那一个鸡蛋需要记录一次操作,所以末尾要加上 1;
每一个新值的计算,都参考了比它行数少,列数少的值,这些值一定是之前已经计算出来的,这样的过程就叫做「状态转移」。
这个问题只是状态转移方程稍显复杂,但空间换时间,逐层递推填表的思想依然是常见的动态规划的思路。
第 3 步:考虑初始化
一般而言,需要 0 这个状态的值,这里 0 层楼和 0 个鸡蛋是需要考虑进去的,它们的值会被后来的值所参考,并且也比较容易得到。
因此表格需要 N + 1 行,K + 1 列。
由于 F 值不会超过最大楼层的高度,要求的是最小值,因此初始化的时候,可以叫表格的单元格值设置成一个很大的数,但是这个数肯定也不会超过当前考虑的楼层的高度。
第 0 行:楼层为 0 的时候,不管鸡蛋个数多少,都测试不出鸡蛋的 F 值,故全为 00;
第 1 行:楼层为 1 的时候,0 个鸡蛋的时候,扔 0 次,1 个以及 1 个鸡蛋以上只需要扔 1 次;
第 0 列:鸡蛋个数为 0 的时候,不管楼层为多少,也测试不出鸡蛋的 F 值,故全为 0,虽然不符合题意,但是这个值有效,它在后面的计算中会被用到;
第 1 列:鸡蛋个数为 1 的时候,这是一种极端情况,要试出 F 值,最少次数就等于楼层高度;
第 4 步:考虑输出
输出就是表格的最后一个单元格的值 dp[N][K]。
import java.util.Arrays;
public class Solution {
public int superEggDrop(int K, int N) {
// dp[i][j]:一共有 i 层楼梯的情况下,使用 j 个鸡蛋的最少实验的次数
// 注意:
// 1、i 表示的是楼层的大小,不是第几层的意思,例如楼层区间 [8, 9, 10] 的大小为 3,这一点是在状态转移的过程中调整的定义
// 2、j 表示可以使用的鸡蛋的个数,它是约束条件,我个人习惯放在后面的维度,表示消除后效性的意思
// 0 个楼层和 0 个鸡蛋的情况都需要算上去,虽然没有实际的意义,但是作为递推的起点,被其它状态值所参考
int[][] dp = new int[N + 1][K + 1];
// 由于求的是最小值,因此初始化的时候赋值为一个较大的数,9999 或者 i 都可以
for (int i = 0; i <= N; i++) {
Arrays.fill(dp[i], i);
}
// 初始化:填写下标为 0、1 的行和下标为 0、1 的列
// 第 0 行:楼层为 0 的时候,不管鸡蛋个数多少,都测试不出鸡蛋的 F 值,故全为 0
for (int j = 0; j <= K; j++) {
dp[0][j] = 0;
}
// 第 1 行:楼层为 1 的时候,0 个鸡蛋的时候,扔 0 次,1 个以及 1 个鸡蛋以上只需要扔 1 次
dp[1][0] = 0;
for (int j = 1; j <= K; j++) {
dp[1][j] = 1;
}
// 第 0 列:鸡蛋个数为 0 的时候,不管楼层为多少,也测试不出鸡蛋的 F 值,故全为 0
// 第 1 列:鸡蛋个数为 1 的时候,这是一种极端情况,要试出 F 值,最少次数就等于楼层高度(想想复杂度的定义)
for (int i = 0; i <= N; i++) {
dp[i][0] = 0;
dp[i][1] = i;
}
// 从第 2 行,第 2 列开始填表
for (int i = 2; i <= N; i++) {
for (int j = 2; j <= K; j++) {
for (int k = 1; k <= i; k++) {
// 碎了,就需要往低层继续扔:层数少 1 ,鸡蛋也少 1
// 不碎,就需要往高层继续扔:层数是当前层到最高层的距离差,鸡蛋数量不少
// 两种情况都做了一次尝试,所以加 1
dp[i][j] = Math.min(dp[i][j], Math.max(dp[k - 1][j - 1], dp[i - k][j]) + 1);
}
}
}
return dp[N][K];
}
}
// 二分查找+dp
```java
import java.util.Arrays;
public class Solution {
public int superEggDrop(int K, int N) {
// dp[i][j]:一共有 i 层楼梯的情况下,使用 j 个鸡蛋的最少仍的次数
int[][] dp = new int[N + 1][K + 1];
// 初始化
for (int i = 0; i <= N; i++) {
Arrays.fill(dp[i], i);
}
for (int j = 0; j <= K; j++) {
dp[0][j] = 0;
}
dp[1][0] = 0;
for (int j = 1; j <= K; j++) {
dp[1][j] = 1;
}
for (int i = 0; i <= N; i++) {
dp[i][0] = 0;
dp[i][1] = i;
}
// 开始递推
for (int i = 2; i <= N; i++) {
for (int j = 2; j <= K; j++) {
// 在区间 [1, i] 里确定一个最优值
int left = 1;
int right = i;
while (left < right) {
// 找 dp[k - 1][j - 1] <= dp[i - mid][j] 的最大值 k
int mid = left + (right - left + 1) / 2;
int breakCount = dp[mid - 1][j - 1];
int notBreakCount = dp[i - mid][j];
if (breakCount > notBreakCount) {
// 排除法(减治思想)写对二分见第 35 题,先想什么时候不是解
// 严格大于的时候一定不是解,此时 mid 一定不是解
// 下一轮搜索区间是 [left, mid - 1]
right = mid - 1;
} else {
// 这个区间一定是上一个区间的反面,即 [mid, right]
// 注意这个时候取中间数要上取整,int mid = left + (right - left + 1) / 2;
left = mid;
}
}
// left 这个下标就是最优的 k 值,把它代入转移方程 Math.max(dp[k - 1][j - 1], dp[i - k][j]) + 1) 即可
dp[i][j] = Math.max(dp[left - 1][j - 1], dp[i - left][j]) + 1;
}
}
return dp[N][K];
}
}
