1. 芯片测试
在讲解具体的芯片测试的分治策略算法之前,先来了芯片测试的意思
1.1 一次测试的过程
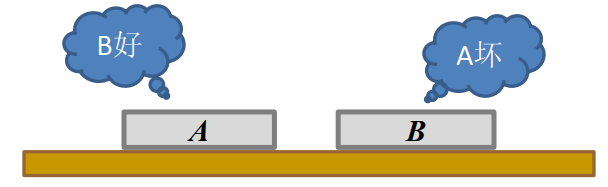
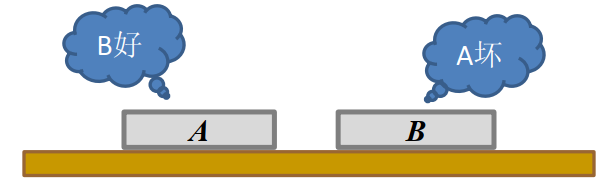
如上图,A、B为芯片。测试方法为:将2片芯片(A和B)置于测试台上,互相进行测试,测试报告是“好”或者“坏”,只取其一。
- 假设:好芯片的报告一定是正确的,坏芯片的报告是不确定的(可能会出错)
那么上述测试的结果有四种可能,如下图:
上面的结果应该不难理解
那么现在问题来了:
- 输入:n片芯片,其中好芯片,至少比坏芯片多一片
- 问题:设计一种测试方法,通过测试从n片中挑出1片好芯片
- 要求:使用最少的测试次数
1.2 如何测试一块芯片的好坏
针对上述问题,现在先来研究一下,如何在上述n片芯片中,测试出A是好芯片还是坏芯片?
- 问题:给定芯片A,判定A的好坏
- 方法:用其他n-1片芯片对A进行测试。
假设:n=7:好芯片数>=4
- A好,6个芯片中至少3个报“好”
- A坏,6个芯片中至少4个报坏
所以对于n是奇数情况下:好芯片数>=(n+1)/2
A好,至少有(n-1)/2个报“好”
A坏,至少有(n+1)/2个报“坏”
结论:
至少一半报好,A是好芯片
超过一半报坏,A是坏芯片
假设: n=8:好芯片数>=5
- A好,7个芯片中至少4个报“好”
- A坏,7个芯片中至少5个报“坏”
所以对于n是偶数:好芯片数 >= n/2+1.
A 好, 至少有 n/2个报告“好”
A 坏, 至少有 n/2+1个报告“坏”
结论:n-1份报告中
至少一半报好,A是好芯片
至少一半报坏,A是坏芯片
上面的分析,已经很清晰,我们已经知道如何测试一块芯片的好坏。那么人们最拿手的方法就是:暴力算法(蛮力算法)可以直接写代码了。。。
1.3 蛮力算法
测试算法:任取 1片测试,如果是好芯片,测试结束;如果是坏芯片,抛弃,再从剩下芯片中任取 1片测试,直到得到 1片好芯片
时间估计:
第一片是坏芯片,最多测试n-2次
第二片是坏芯片,最多测试n-3次
…
总计:Θ(n^2 )
#include<iostream>
#include<cmath>
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <cstring>
#define MAX 100
using namespace std;
int main(){
int n;
int a[MAX];
while(cin>>n){
srand(time(NULL));
memset(a,0,sizeof(a));
for(int i=1;i<=n;i++){ /*芯片编号为数组下标,从1开始*/
cin>>a[i]; /*数组值代表芯片好坏,1为真0为假*/
}
int cnt=0; /*查找次数*/
for(int i=1;i<=n;i++){
int sum=0;
for(int j=1;j<=n;j++){
cnt++;
if(i!=j&&a[i]==1&&a[j]==1) /*两片芯片都是好的*/
sum++;
if(i!=j&&a[i]==1&&a[j]==0) /*测试芯片是坏的*/
sum+=rand()%2;
if(i!=j&&a[i]==0&&a[j]==0) /*两片芯片都是坏的*/
sum+=rand()%2;
}
if(sum>=n/2){
cout<<"查找次数:"<<cnt<<endl;
break;
}
}
}
return 0;
}
可见时间复杂度之高,数据量一多,肯定会超时。
1.4 分治算法设计思想
在分析分治算法的正确性之前,我们先给出这个算法的描述:
假设n为偶数,将n片芯片两两一组做测试淘汰,剩下芯片构成子问题,进入下一轮分组淘汰。
淘汰规则为:
- “好,好” ==> 任留1片,进入下轮
- 其他情况 ==> 全部抛弃
递归截止条件:n<=3
3片芯片,一次测试可得到好芯片
1或者2片芯片,不需要再测试,他们都为好芯片。
上述算法过程就是我们给出的分治策略的设计。那么为什么上述的策略是正确的呢?
回忆一下,前面的文章,要保证分治策略的正确性的基本条件是:子问题与原问题性质相同。下面我们就来证明,上述分治策略的子问题与原问题性质相同。
1.41 分治算法的正确性证明
原问题:n片芯片,其中好芯片,至少比坏芯片多一片
那么子问题,命题1:当 n 是偶数时,在上述淘汰规则下,经过一轮淘汰,剩下的好芯片比坏芯片至少多1片
我们需要证明上述子问题的命题1是正确的。
证明:假设原问题中A,B都好的芯片有i组,A与B一好一坏的有j组,A与B都坏的有k组。那么经过一轮淘汰后,好芯片还剩i片,坏芯片还剩k片。
因为
- 初始芯片总数 2i+2j+2k = n
- 初始好芯片多于坏芯片:2i+j > 2k+j
得出:i>k
所以,剩余的芯片好芯片比坏芯片,至少多1片。命题1 是正确的。即证明了上述分治算法的正确性。
当n为奇数时,特殊处理。当n是奇数时,可能会出现问题,如图:
可见淘汰后的子问题并不满足于原问题性质相同,此时无法继续测试。
- 处理办法是:当n为奇数时,增加一轮对轮空芯片的单独测试,如果该轮空芯片为好芯片则算法结束,如果是坏芯片,则淘汰该芯片。
下面给出上述分治算法的伪码描述:

补充说明:
- 第6点:
if(1好1坏),则说明测试的两个至少一个为坏,所以未参加测试的一定为好的 - 第7点:由于题目初始条件,好的芯片一定比坏的芯片多
1.42 时间复杂度分析
设输入规模为n,,每轮淘汰后,芯片数至少减半,测试次数(含轮空处理):O(n)
时间复杂度:
W(n) = W(n/2) + O(n)
W(3)=1,W(2)=W(1)=0
解上述方程的得:W(n) = O(n)
结果很振奋人心,你已经将一个O(n^2)级别的算法优化为了O(n)O(n)O(n)级别!!!
2. 总结
最大的需要注意的地方就是:如何保证子问题与原问题性质相同:
可以:
- 增加额外处理(比如上述n为奇数时对轮空数据的处理)
- 额外处理的工作量,不改变函数的阶
#include<iostream>
#include <cmath>
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <cstring>
#define MAX 100
using namespace std;
int main(){
int n;
int num1,num2,sum;
int a[MAX],b[MAX];
while(cin>>n){
srand(time(NULL));
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
/*a数组标记芯片好坏,b数组记录被保留芯片编号*/
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=i;
}
num1=n;
num2=1;
sum=0;
while(1){
/*芯片只剩一片或两片则可以直接得到结果,结束循环*/
if(num1<=2)
break;
else if(num1%2){ /*芯片个数为奇数*/
for(int i=1;i<num1;i+=2){
sum++; /*记录查找次数*/
if(a[b[i]]==1&&a[b[i+1]]==1) /*两片芯片都是好的*/
b[num2++]=b[i+rand()%2];
/*两片芯片是坏的,rand模拟结果是好的这一随机现象*/
if(a[b[i]]==0&&a[b[i+1]]==0&&rand()%2)
b[num2++]=b[i+rand()%2];
}
b[num2++]=b[num1]; /*最后一块芯片保留*/
}
else{ /*芯片个数为偶数*/
for(int i=1;i<=num1;i+=2){
sum++;
if(a[b[i]]==1&&a[b[i+1]]==1) /*两片芯片都是好的*/
b[num2++]=b[i+rand()%2];
if(a[b[i]]==0&&a[b[i+1]]==0&&rand()%2) /*两片芯片是坏的*/
b[num2++]=b[i+rand()%2];
}
}
num1=num2-1; /*一次比较后保留芯片的个数*/
num2=1; /*下一次查找的开始位置*/
}
cout<<"查找次数:"<<sum<<endl;
cout<<"找到的芯片编号:"<<b[1]<<endl;
}
return 0;
}
参考链接:https://www.jianshu.com/p/1cec17bfb2d5
参考链接:https://blog.csdn.net/qq_37375427/article/details/102529005

