平衡树学习小结

平衡树学习小结

回忆往昔，感触良多，看到了之前自己啥都不会的优雅的数据结构，还有，逝去的青春，和不思进取的现在，写一个学习笔记，仅供自己参考，因为，不一定正确。

本文涉及了以下内容

• AVL树
• 自顶向下伸展树
• fhq_treap
• ScapeGoat Tree

前言

记得是寒假的一个早上，闲的没事干，和 Singercoder 研究了一下，自学啥好？于是，便决定了，要挖掘平衡树这棵宝藏。现在想想，或许只是年少轻狂罢了。

AVL

我学的第一个平衡树，花了我一周的时间，他在 《数据结构与算法分析》 中被作为 BST 之后的下一章，作为基础数据结构被提及。

他是平衡树的老祖宗了，咋说呢？效率仅次于红黑树，因为红黑树保证了每一个子树的高度不超过 \(2\lg n\) 于是做到了很优的时间，他是 AVL 的变种，但是 AVL 树的平衡树条件显得显而易见，所以作为第一种平衡树在 1962 年的时候被 (Adelson-Velskii & Landis) 提出。

BST 是平均可以做到单次操作 \(\lg n\) 的复杂度的，注意是平均，因为毒瘤出题人会把你卡的心态爆炸。

一种简单的想法就是限定左右子树的高度必定完全一样，但是这太苛刻了，不能实现，所以不妨放开条件，令左右子树的高度最多差一，于是 AVL树 就诞生了。也是由于这个条件，他需要存储令人抓狂的 height 信息，这往往会造成访问非法内存导致的莫名 Runtime error。这也限定了它的实现方式必须是自底向上，从而导致了即是它效率优秀，但是在 OI 中并不被人们使用的原因。毕竟许多平衡树的操作也是 \(\lg n\) 的

于是我们得到他的结点声明

struct avlNode;
typedef avlNode *avl;
struct avlNode
{
	avl ls, rs;
	int size, height, num;
	KYN data;
	void update() 
	{
		this->size = this->ls->size + this->rs->size + this->num;
		this->height = max(this->ls->height ,this->rs->height) + 1;
	}
};

其中 KYN 也只是以 Elem 类型罢了（真的。ls 是指左儿子，rs 同理，然后 num 是指频数，height 为这个结点的深度， size 是指这个结点为根的子树大小。

我们知道，这种把update写在结构体里边的行为是不明智的，所以我们常常用 NullNode 结点来代替 NULL 来避免 RE 和提高程序的效率，这也被称为哨兵结点。

我们类比 BST 的插入方式，可以得到它的 insert 函数，问题是如何维护左右子树高度差的性质？

只要在 insert 之后的那个时候加一个判断是否平衡，如果不是就通过旋转来维护性质

旋转

平衡树用了四种旋转来维护性质，所以根据对称的，我们只介绍两种足以，事实上在实现的时候只需要实现两个单旋即可，甚至更离谱的用数组存二叉树的孩子可以用位运算来把函数个数进一步减少

单旋

下图给出了左单旋的例子

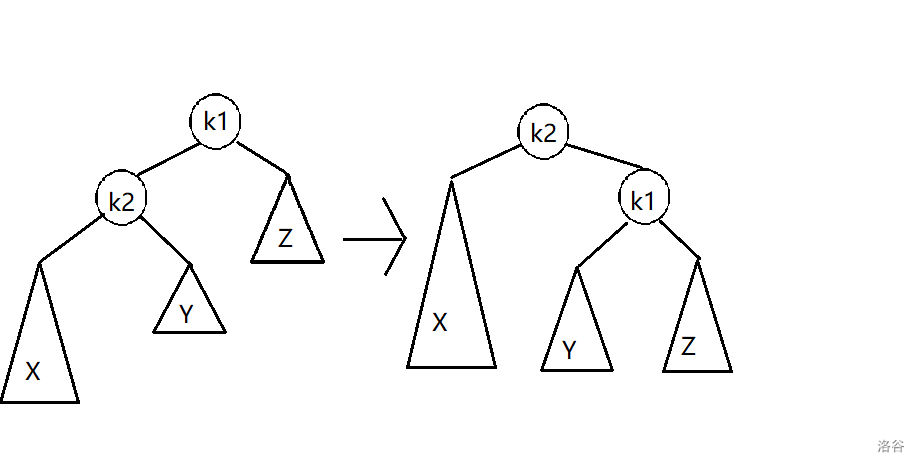
正如上图所示，旋转确实减少了树的深度，我们如何描述旋转的过程，想象一下，正如 ydc 所说的从生物学上看这是一棵树，你抓住他的 k2 结点，然后枝条自然是柔软而灵活的，所以 Y 便滑到了 k1 处成为了他的左孩子，那么，右单旋也是对称的，不难理解

双旋

下图给出了做左双旋的例子

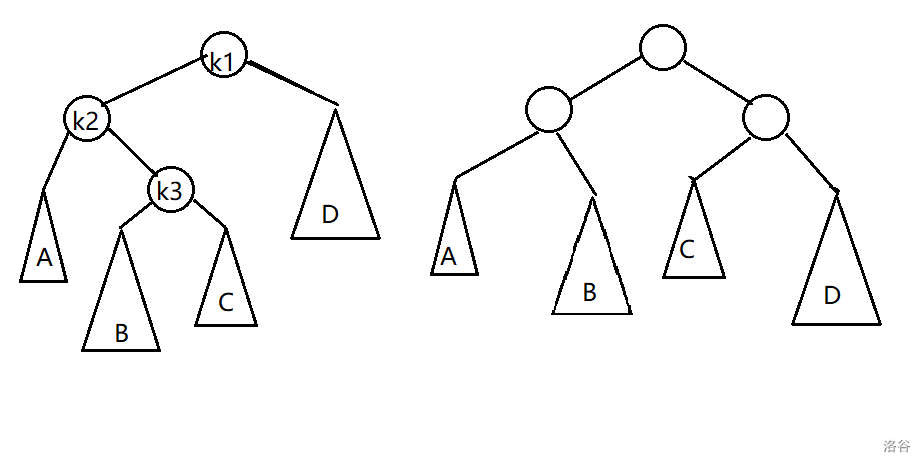
有了上边的铺垫，这就显然了许多，对于 k2 结点做一次右单旋，对于 k1 再做左单旋，就 ok 了

于是我们的旋转可以记为：做什么旋，就把什么儿子旋转到自己的头顶当爸爸，而自己成为另一个什么的儿子

下面给出旋转的代码

inline avl Single_left(avl T)
{
	avl a = T->ls;
	T->ls = a->rs;
	a->rs = T;
	T->update();
	a->update();
	return a;
}

inline avl Single_right(avl T)
{
	avl a = T->rs;
	T->rs = a->ls;
	a->ls = T;
	T->update();
	a->update();
	return a;
}

inline avl double_left(avl T)
{
	T->ls = Single_right(T->ls);
	return Single_left(T);
}

inline avl double_right(avl T)
{
	T->rs = Single_left(T->rs);
	return Single_right(T);
}

小的优化

内存池的写法让指针焕然新生

avl rot, null, tot, deleted[Maxn];
avlNode memory[Maxn];
int deltop;
inline avl init(KYN x)
{
	avl tmp = deltop ? deleted[deltop--] : tot++;
	tmp->ls = tmp->rs = null;
	tmp->size = tmp->num = tmp->height = 1;
	tmp->data = x;
	return tmp;// 一定要写的，不然开o2就玩完
}

删除和插入

简单分析，插入和删除的代码，结合注释你可以清楚明白整个过程

avl insert(avl T, KYN x)
{
	if(T == null) return init(x);// 没有说明到了最下边
	if(x == T->data)
	{
		++(T->num);// 如果原来有这个元素
		T->update();// 更新
		return T;
	}
	if(x < T->data)
	{
		T->ls = insert(T->ls, x);// 在左边插
		T->update();// 更新
		if(T->ls->height - T->rs->height == 2)
		{
			if(x < T->ls->data) T = Single_left(T);// 左单旋，如果插在左边的左边
			else T = double_left(T);// 插在左边的右边

		}
	}
	else
	{
		T->rs = insert(T->rs, x);// 右边
		T->update();// 更新，其余同理
		if(T->rs->height - T->ls->height == 2)
		{
			if(T->rs->data < x) T = Single_right(T);
			else T = double_right(T);
		}
	}
	return T;
}
	
avl erase(avl T, KYN x)
{
	if(T == null) return null;
	if(x < T->data)
	{
		T->ls = erase(T->ls, x);// 左边删
		T->update();// 更新
		if(T->rs->height - T->ls->height == 2)
		{
			if(T->rs->rs->height >= T->rs->ls->height) T = Single_right(T);// 
			else T = double_right(T);
		}
	}
	else if(T->data < x)
	{
		T->rs = erase(T->rs, x);
		T->update();
		if(T->ls->height - T->rs->height == 2)
		{
			if(T->ls->ls->height >= T->ls->rs->height) T = Single_left(T);
			else T = double_left(T);
		}
	}
	else
	{
		if(T->num > 1)
		{
			--(T->num);// 有多余的就频数-1就好了
			T->update();
			return T;
		}
		if(T->ls != null && T->rs != null)// 两个孩子都有
		{
			avl p = T->rs;
			while(p->ls != null) p = p->ls;// 找到右边的的最左边，拎上来
			T->num = p->num;
			T->data = p->data, p->num = 1;
			T->rs = erase(T->rs, T->data);
			T->update();
			if(T->ls->height - T->rs->height == 2)
			{
				if(T->ls->ls->height >= T->ls->rs->height) T = Single_left(T);
				else T = double_left(T);
			}
		}
		else
		{
			avl p = T;// 没有直接拎上来就好了
			if(T->ls != null) T = T->ls;
			else if(T->rs != null) T = T->rs;
			else T = null;
			deleted[++deltop] = p;
		}
	}
	return T;
}

前驱和后继

好了直接给出前驱和后继和查找的方法（和BST无异）

avl find(avl T, KYN x)
{
	while(T != null)
	{
		if(T->data == x) return T;
			else if(T->data > x) T = T->ls;
			else T = T->rs;
	}
	return null;
}
	
KYN prv(KYN x)
{
	KYN ans = KYN(-1 << 30);
	avl tmp = rot;
	while(tmp != null)
	{
		if(tmp->data == x)
		{
			if(tmp->ls != null)
			{
				tmp = tmp->ls;
				while(tmp->rs != null) tmp = tmp->rs;
				ans = tmp -> data;
			}
			break;
		}
		if(tmp->data < x && ans < tmp->data) { ans = tmp->data;
		tmp = tmp->data < x ? tmp->rs : tmp->ls;
	}
	return ans;
}
	
KYN next(KYN x)
{
	KYN ans = KYN(1 << 30);
	avl tmp = rot;
	while(tmp != null)
	{
		if(tmp->data == x)
		{
			if(tmp->rs != null)
			{
				tmp = tmp->rs;
				while(tmp->ls != null) tmp = tmp->ls;
				ans = tmp->data;
			}
			break;
		}
		if(x < tmp->data && tmp->data < ans) ans = tmp->data;
		tmp = tmp->data < x ? tmp->rs : tmp->ls;
	}
	return ans;
}

Kth 和 rank

那么 Kth 和 rank 操作也十分显然

KYN get_rank(avl T, KYN x) 
{
	int ans = 0;
	while(T != null)
	{
		if(T->data == x) return ans + T->ls->size + 1;
		else if(x < T->data) T = T->ls;
		else ans += T->ls->size + T->num, T = T->rs;
	}
	return ans + 1;
}

KYN get_data(avl T, int rank)
{
	while(T != null)
	{
		if(T->ls->size >= rank) T = T->ls;
		else if(T->ls->size + T->num >= rank) return T->data;
		else rank -= T->num + T->ls->size, T = T->rs;
	}
}

那么 AVL 树的操作到此为止。

ScapeGoat Tree

体现了数据结构的暴力优雅。核心思想是懒惰删除 + 暴力重构

我们定义一个结点的好坏，当且仅当它满足平衡因子，并且树里至少有十分之一的点是有价值的

给出ScapeGoat Tree结点的声明

struct sgtNode;
typedef sgtNode *sgt;
struct sgtNode
{
	sgt ls, rs;
	int size, valid;
	name data;
	bool del;
	inline bool bad() { return (db) ls->size > alpha * (db) size || (db) rs->size > alpha * (db) size || valid * 10 <= size; }
	inline void update() { size = ls->size + rs->size + !del; valid = ls->valid + rs->valid + !del; }
};

我们得出一个暴力重构的函数，这几乎不需要动脑子

void dfs(sgt T, vector <sgt> &ve)
{
	if(T == null) return ;
	dfs(T->ls ,ve);
	if(!T->del) ve.push_back(T);
	dfs(T->rs, ve);
	if(T->del) delete T;
}
		
sgt build(int l, int r, vector <sgt> &ve)
{
	if(l > r) return null;
	int mid = (l + r) >> 1;
	sgt T = ve[mid];
	T->ls = build(l, mid - 1, ve);
	T->rs = build(mid + 1, r, ve);
	T->update();
	return T;
}

void rebuild(sgt &T)
{
	vector <sgt> ve;
	dfs(T, ve);
	T = build(0, ve.size() - 1, ve);
	return ;
}

注意传参的形式
那么 insert() 和 erase() 函数我们都可以简单的写出

void insert(sgt &T, name x)
{
	if(T == null)
	{
		T = init(x);
		return;
	}
	++(T->size);
	++(T->valid);
	if(x < T->data) insert(T->ls, x);
	else insert(T->rs, x);
	if(T->bad()) rebuild(T);
	return;
}

void erase(sgt &T, int rk)
{
	if(T == null) return;
	if(!T->del && rk == T->ls->valid + !T->del) {
		T->del = 1;
		--(T->valid);
		return;
	}
	--(T->valid);
	if(rk <= T->ls->valid + !T->del) erase(T->ls, rk);
	else erase(T->rs, rk - T->ls->valid - !T->del);
	return;
}

给出一个简单的前驱和后继的写法

inline int prv(name x) { return get_data(get_rank(x) - 1); }
inline int next(name x) { return get_data(get_rank(x + 1)); }

啥意思？一个结点的前驱自然是它减一的排名的内容了，而后继不难理解。

替罪羊显然是十分高效的除了rebuild可能常数略大之外都还好；

fhq_treap

与 Treap 类似他的期望时间复杂度也是 \(\lg n\) 但实际会比 Treap 跑的慢，因为利用了递归。这导致系统要为他分配栈空间。
那么它的实现短小精悍，这正是oi所需要的，尽管它只是期望。

它最大的强大不是做裸题，而是它可以维护数列，这是除了 splay 之外的树所没有的，但是比 splay 要强的是它还支持可持久化。

所以总结一下这个东西的优点：短小精悍，可持久化，维护数列。而缺点：常数略大，容易被卡。

但是，事实上也只有大样例可以卡掉fhq_Treap，所以往往在考试中用是一个不错的选择。

练好 fhq_treap 天下我有

那么 fhq_treap 自然与 Treap 脱不了干系，就在 rad 上满足了堆的性质，而 Elem 上 满足 BST
所以这玩意就很玄学了。

它通过不断地 split 和 merge 来做操作，同时splIt 有两种，一种是根据 Elem，另一种是根据 Size

给出结点定义

struct Node;
typedef Node *node;
#define pnn pair <node, node>
struct Node
{
	node son[2];
	int size, val, rad;
	void maintain()
	{	
		this->size = this->son[0]->size + this->son[1]->size + 1;
		return void();
	}
};

随之是 merge 和 split

pnn split(node T, int k)
	{
		if(T == null) return mkp(null, null);
		pnn t;
		if(k < T->val)
		{
			t = split(T->son[0], k);
			T->son[0] = t.second;
			T->maintain();
			t.second = T;
		}
		else
		{
			t = split(T->son[1], k);
			T->son[1] = t.first;
			T->maintain();
			t.first = T;
		}
		return t;
	}
	
	node merge(node x, node y)
	{
		if(x == null) return y;
		if(y == null) return x;
		if(x->rad < y->rad)
		{
			x->son[1] = merge(x->son[1], y);
			x->maintain();
			return x;
		}
		else
		{
			y->son[0] = merge(x, y->son[0]);
			y->maintain();
			return y;
		}
	}

自顶向下伸展树

无论是自顶向下还是自底向上的，他的均摊复杂度是 \(O(\lg n)\) 的也就是说，会有的时候的操作是 \(O(n)\) 的。

与网上其他的笔记不同，我是学的是自顶向下的，所以旋转会很简单。

下图解释了为什么简单

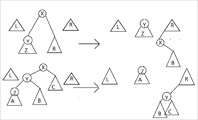
好吧，我承认我学不会 splay 那我学个自顶向上的不行？这玩意常数小于 fhq-treap 的。

Splay 有六个旋转，但事实上写两个就够了。

于是给出 splay 的代码和 insert 和 remove 值得一提的是remove 需要 nxt 和 pre 的例程

class SplayTree
{
	private:
		
		struct
		SplayNode
		{
			SplayNode *Son[2];
			int Elem;
		};
		typedef SplayNode* node;
		
	protected:
		
		node Tot, Rot, Null, Del[Maxn];
		SplayNode Memory[Maxn];
		int Deltop;
		
		node
		init( int item )
		{
			node Tmp = Deltop ? Del[ Deltop-- ] : Tot++;
			Tmp->Son[ 0 ] = Tmp->Son[ 1 ] = Null;
			Tmp->Elem = item;
			return Tmp;
		}
		
		node
		Singleleft( node X )
		{
			node Y = X->Son[ 0 ];
			X->Son[ 0 ] =  Y->Son[ 1 ];
			Y->Son[ 1 ] = X;
			return Y;
		}
		
		node
		Singleright( node X )
		{
			node Y = X->Son[ 1 ];
			X->Son[ 1 ] = Y->Son[ 0 ];
			Y->Son[ 0 ] = X;
			return Y;
		}
		
		node
		Splay( int item, node T )
		{
			SplayNode Header;
			node leftmax, rightmin;
			leftmax = rightmin = &Header;
			Null->Elem = item;
			while( T->Elem != item )
			{
				if( item < T->Elem )
				{
					if( item < T->Son[ 0 ]->Elem )
						T = Singleleft( T );
					if( T->Son[ 0 ] == Null )
						break;
					rightmin = ( rightmin->Son[ 0 ] = T );
					T = T->Son[ 0 ];
				}
				else
				{
					if( T->Son[ 1 ]->Elem < item )
					T = Singleright( T );
					if( T->Son[ 1 ] == Null )
						break;
					leftmax = ( leftmax->Son[ 1 ] = T );
					T = T->Son[ 1 ];
				}
			}
			leftmax->Son[ 1 ] = T->Son[ 0 ];
			rightmin->Son[ 0 ] = T->Son[ 1 ];
			T->Son[ 0 ] = Header.Son[ 1 ];
			T->Son[ 1 ] = Header.Son[ 0 ];
			return T;
		}
		
		node
		insert( int x, node T )
		{
			node Tmp = init( x );
			if( T == Null )
				return Tmp;
			else
			{
				T = Splay( x, T );
				if( x < T->Elem )
				{
					Tmp->Son[ 0 ] = T->Son[ 0 ];
					Tmp->Son[ 1 ] = T;
					T->Son[ 0 ] = Null;
					T = Tmp;
				}
				else
				{
					Tmp->Son[ 1 ] = T->Son[ 1 ];
					Tmp->Son[ 0 ] = T;
					T->Son[ 1 ] = Null;
					T = Tmp;
				}
			}
			return T;
		}
		
		node
		Find( int x, node T )
		{
			T = Splay( x, T );
			return T;
		}
		
		node
		pre( int x, node T )
		{
			T = Find( x, T );
			Rot = T;
			if( T->Elem >= x )
			{
				T = T->Son[ 0 ];
				while( T->Son[ 1 ] != Null ) T = T->Son[ 1 ];
			}
			return T;
		}
		
		node
		nxt1( int x, node T )
		{
			T = Splay( x, T );
			Rot = T;
			if( T->Elem < x )
			{
				T = T->Son[ 1 ];
				while( T->Son[ 0 ] != Null ) T = T->Son[ 0 ];
			}
			return T;
		}
		
		
		node
		pre1( int x, node T )
		{
			T = Find( x, T );
			Rot = T;
			if( T->Elem > x )
			{
				T = T->Son[ 0 ];
				while( T->Son[ 1 ] != Null ) T = T->Son[ 1 ];
			}
			return T;
		}
		
		node
		nxt( int x, node T )
		{
			T = Splay( x, T );
			Rot = T;
			if( T->Elem <= x )
			{
				T = T->Son[ 1 ];
				while( T->Son[ 0 ] != Null ) T = T->Son[ 0 ];
			}
			return T;
		}
		
		node
		remove( int x, node T )
		{
			node lt = pre( x, Rot );
			node rt = nxt( x, Rot );
			Rot = lt = Splay( lt->Elem , Rot );
			lt->Son[ 1 ] = Splay( rt->Elem, lt->Son[ 1 ] );
			Del[ ++Deltop ] = rt->Son[ 0 ];
			rt->Son[ 0 ] = Null;
			return lt;
		}
		
	public:
		
		SplayTree(  )
		{
			Tot = Memory;
			Null = Tot++;
			Null->Son[ 0 ] = Null->Son[ 1 ] = Null;
			Rot = Null;
			Deltop = 0;
		}
		
		void
		insert( int x )
		{
			Rot = insert( x, Rot );
		}
		
		void
		remove( int x )
		{
			Rot = remove( x, Rot );
		}
		
		int
		pre( int x )
		{
			node Tmp = pre1( x, Rot );
			return Tmp->Elem;
		}
		
		int
		nxt( int x )
		{
			node Tmp = nxt1( x, Rot );
			return Tmp->Elem;
		}
};