论文标题:Class-Balanced Loss Based on Effective Number of Samples https://github.com/vandit15/Class-balanced-loss-pytorch/blob/master/class_balanced_loss.py https://arxiv.org/pdf/1901.05555.pdf pytorch+resnet18实现长尾数据集分类
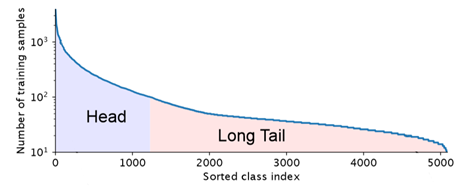
类别不平衡问题 现实世界的数据集,大部分都是分布不均匀的,几个主导类别拥有大量样本,而大多数其他的类别只有着相对较少的样本。使用这种长尾数据集训练CNNs时,模型在弱表示类中表现较差。
类别不平衡的处理策略: 通常情况下,对于长尾数据集,有以下两种应对策略
1.重新采样 理论及代码链接 2.成本敏感学习
提出问题 如何找到合适的权重赋值方法,提高分类损失函数的效果?
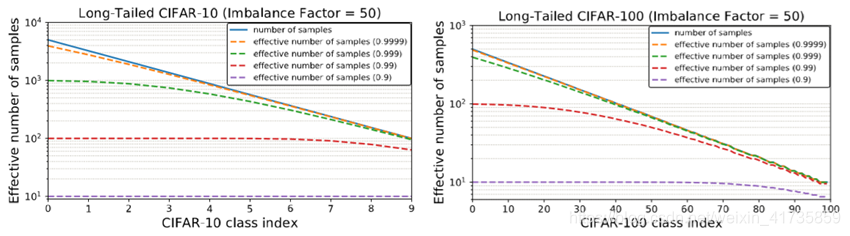
边际效应 随着数据量增加,模型新增的收益越来越少
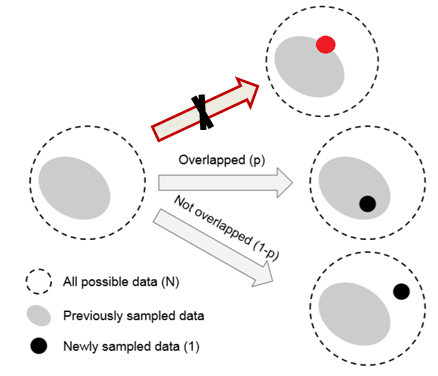
数据采样和随机覆盖 一个类中,该类样本空间中所有可能数据 的集合为
S
S
S
S
S
S 样本体积 为
N
N
N
S
S
S
S
S
S
S
S
S
S
S
S
N
N
N
定义 有效样本量是样本的期望体积
S
S
S
S
S
S 独一无二 的样本的集合称为有效样本量,也就是样本的期望体积。 对于独一无二的样本:1+1=2。
命题 计算有效样本量的方法:
E
n
=
(
1
−
β
n
)
/
(
1
−
β
)
E_{n}=\left(1-\beta^{n}\right) /(1-\beta)
E n = ( 1 − β n ) / ( 1 − β )
n
n
n
N
N
N
β
=
(
N
−
1
)
/
N
\beta=(N-1) / N
β = ( N − 1 ) / N 数学归纳法
n
n
n
E
1
=
(
1
−
β
1
)
/
(
1
−
β
)
=
1
E_{1}=\left(1-\beta^{1}\right) /(1-\beta)=1
E 1 = ( 1 − β 1 ) / ( 1 − β ) = 1
假设
E
n
−
1
=
(
1
−
β
n
−
1
)
/
(
1
−
β
)
E_{n-1}=\left(1-\beta^{n-1}\right) /(1-\beta)
E n − 1 = ( 1 − β n − 1 ) / ( 1 − β )
n
n
n
n
−
1
n-1
n − 1
p
=
E
n
−
1
/
N
p=E_{n-1} / N
p = E n − 1 / N
n
n
n
E
n
−
1
E_{n-1}
E n − 1
n
n
n
E
n
−
1
+
1
E_{n-1} + 1
E n − 1 + 1
E
n
=
p
E
n
−
1
+
(
1
−
p
)
(
E
n
−
1
+
1
)
E_{n}=p E_{n-1}+(1-p)\left(E_{n-1}+1\right)
E n = p E n − 1 + ( 1 − p ) ( E n − 1 + 1 )
=
(
1
−
β
n
)
/
(
1
−
β
)
=
∑
j
=
1
n
β
j
−
1
=\left(1-\beta^{n}\right) /(1-\beta)=\sum_{j=1}^{n} \beta^{j-1}
= ( 1 − β n ) / ( 1 − β ) = ∑ j = 1 n β j − 1
n
→
∞
,
E
n
=
1
/
(
1
−
β
)
=
N
\mathrm{n} \rightarrow \infty, E_{n}=1 /(1-\beta)=\mathrm{N}
n → ∞ , E n = 1 / ( 1 − β ) = N 样本中采样的样本足够多时,有效样本量数目等于样本体积。 同时也符合之前
β
\beta
β
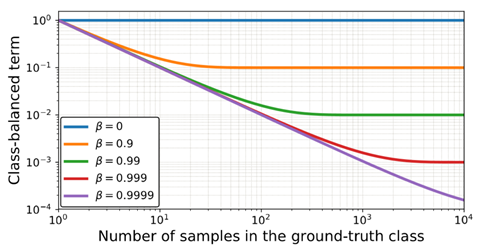
推论:渐近性
β
=
0
(
N
=
1
)
,
E
n
=
1
\beta=0(N=1), \quad E_{n}=1
β = 0 ( N = 1 ) , E n = 1
β
→
1
(
N
→
∞
)
,
E
n
→
n
\beta \rightarrow 1(N \rightarrow \infty), \quad E_{n} \rightarrow n
β → 1 ( N → ∞ ) , E n → n
证明:
β
=
0
,
E
n
=
(
1
−
0
n
)
/
(
1
−
0
)
=
1
\beta=0, \quad E_{n}=\left(1-0^{n}\right) /(1-0)=1
β = 0 , E n = ( 1 − 0 n ) / ( 1 − 0 ) = 1
β
→
1
,
\beta \rightarrow 1, \quad
β → 1 ,
f
(
β
)
=
1
−
β
n
,
g
(
β
)
=
1
−
β
f(\beta)=1-\beta^{n}, g(\beta)=1-\beta
f ( β ) = 1 − β n , g ( β ) = 1 − β
lim
β
→
1
f
(
β
)
=
lim
β
→
1
g
(
β
)
=
0
\lim _{\beta \rightarrow 1} f(\beta)=\lim _{\beta \rightarrow 1} g(\beta)=0
lim β → 1 f ( β ) = lim β → 1 g ( β ) = 0 洛必达法则
E
n
=
n
E_{n}=n
E n = n 样本体积
N
N
N
类平衡损失函数 原文说到:The proposed effective number of samples for class
i
i
i
E
n
i
=
(
1
−
β
i
n
i
)
/
(
1
−
β
i
)
,
E_{n_{i}}=\left(1-\beta_{i}^{n_{i}}\right) /\left(1-\beta_{i}\right),
E n i = ( 1 − β i n i ) / ( 1 − β i ) ,
β
i
=
(
N
i
−
1
)
/
N
i
.
\beta_{i}=\left(N_{i}-1\right) / N_{i} .
β i = ( N i − 1 ) / N i . Without further information of data for each class, it is difficult to empirically find a set of good hyperparameters
N
i
N_{i}
N i Therefore, in practice, we assume
N
i
N_{i}
N i
N
i
=
N
,
β
i
=
β
=
(
N
−
1
)
/
N
N_{i}=N, \beta_{i}=\beta=(N-1) / N
N i = N , β i = β = ( N − 1 ) / N
N
i
N_{i}
N i
N
i
N_{i}
N i
N
N
N
N
i
N_{i}
N i 类平衡损失函数:
C
B
(
p
,
y
)
=
1
E
n
L
(
p
,
y
)
=
1
−
β
1
−
β
n
y
L
(
p
,
y
)
\mathrm{CB}(\mathrm{p}, y)=\frac{1}{E_{n}} L(\mathrm{p}, y)=\frac{1-\beta}{1-\beta^{n} y} L(\mathrm{p}, y)
C B ( p , y ) = E n 1 L ( p , y ) = 1 − β n y 1 − β L ( p , y )
1
E
n
\frac{1}{E_{n}}
E n 1
L
(
p
,
y
)
L(\mathrm{p}, y)
L ( p , y )
Softmax:
C
E
s
o
f
t
m
a
x
(
z
,
y
)
=
−
1
−
β
1
−
β
n
y
log
(
exp
(
z
y
)
∑
j
=
1
C
exp
(
z
j
)
)
.
\mathrm{CE}_{\mathrm{softmax}}(\mathrm{z}, y)=-\frac{1-\beta}{1-\beta^{n_{y}}} \log \left(\frac{\exp \left(z_{y}\right)}{\sum_{j=1}^{C} \exp \left(z_{j}\right)}\right).
C E s o f t m a x ( z , y ) = − 1 − β n y 1 − β log ( ∑ j = 1 C exp ( z j ) exp ( z y ) ) .
Sigmoid:
C
B
sigmoid
(
z
,
y
)
=
−
1
−
β
1
−
β
n
y
∑
i
=
1
C
log
(
1
1
+
exp
(
−
z
i
t
)
)
\quad \mathrm{CB}_{\text {sigmoid }}(\mathrm{z}, y)=-\frac{1-\beta}{1-\beta^{n_{y}}} \sum_{i=1}^{C} \log \left(\frac{1}{1+\exp \left(-z_{i}^{t}\right)}\right)
C B sigmoid ( z , y ) = − 1 − β n y 1 − β ∑ i = 1 C log ( 1 + exp ( − z i t ) 1 )
Focal loss:
\quad
(
z
,
y
)
=
−
α
t
(
1
−
p
t
)
γ
log
(
p
t
)
(\mathrm{z}, y) \quad=-\alpha_{\mathrm{t}}\left(1-p_{t}\right)^{\gamma} \log \left(p_{t}\right)
( z , y ) = − α t ( 1 − p t ) γ log ( p t )
\quad
C
B
focal
(
z
,
y
)
=
−
1
−
β
1
−
β
n
y
∑
i
=
1
C
(
1
−
p
i
t
)
γ
log
(
p
i
t
)
\mathrm{CB}_{\text {focal }}(\mathrm{z}, y)=-\frac{1-\beta}{1-\beta^{n} y} \sum_{i=1}^{C}\left(1-p_{i}^{t}\right)^{\gamma} \log \left(p_{i}^{t}\right)
C B focal ( z , y ) = − 1 − β n y 1 − β ∑ i = 1 C ( 1 − p i t ) γ log ( p i t )
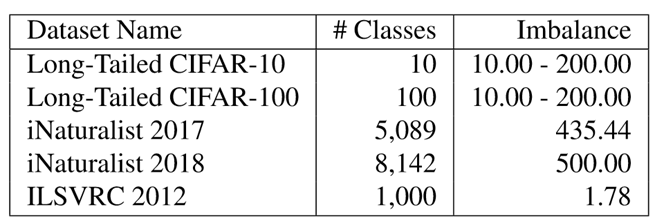
实验数据 CIFAR-10和CIFAR-100都是平衡数据集,作者通过删减数据的方式,将其变为长尾数据集。
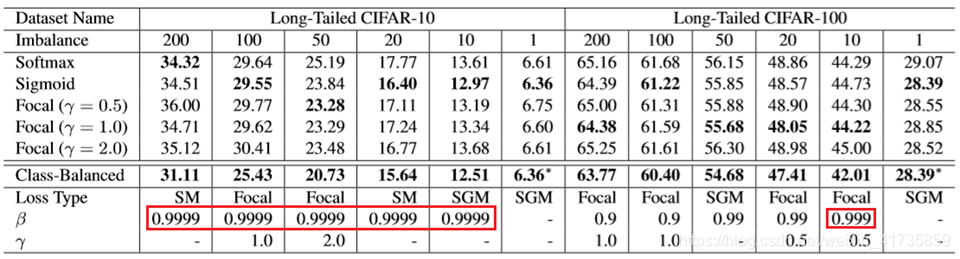
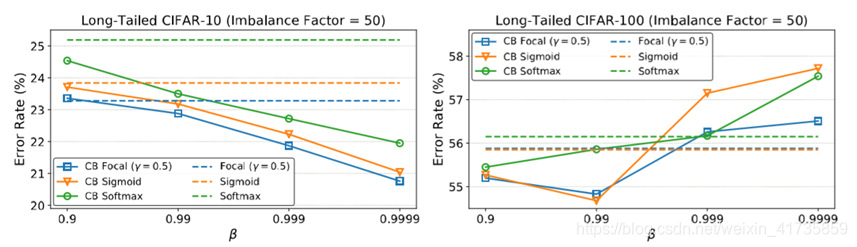
实验结果1(小数据集) 实验分析1
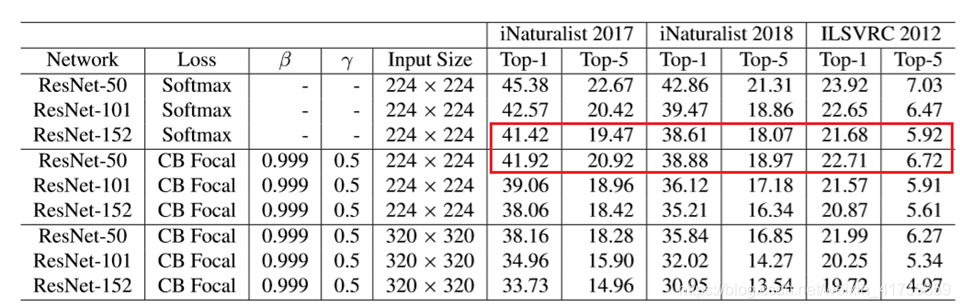
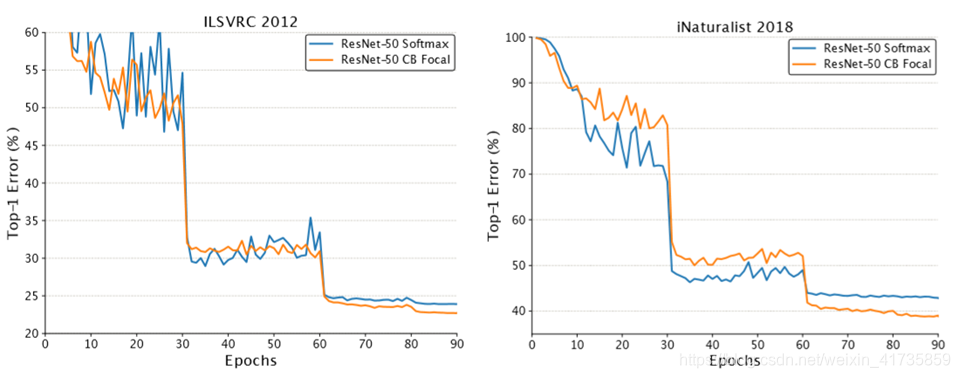
实验结果2(大数据集) 实验分析2
结论
论文从定义,命题,推论,实验中充分说明了作者提出的类别不平衡因子的有效性。
论文也有许多不足之处,虽然理论部分提出并证明了样本体积
N
N
N
β
β
β
β
β
β
β
β
β
论文解读应该存在问题,望指正!!!论文翻译参考链接