概率论：协方差矩阵

一、协方差矩阵

1.1 从方差/协方差到协方差矩阵

根据方差的定义，给定 $d$个随机变量 $x_k,i=1,2,...,d$，则这些随机变量的方差为：

$\sigma(x_k,x_k)={1\over n-1}\sum_{i=i}^n(x_{ki}-\overline{x}_k)^2$

其中 $x_{ki}$表示随机变量 $x_k$中的第 $i$个观测样本， $n$表示样本量，每个随机变量所对应的观测样本数均为 $n$

对于这些随机变量，我们还可以根据协方差的定义，求出两两之间的协方差，即：

$\sigma(x_m,x_k)={1\over n-1}\sum_{i=1}^n(x_{mi}-\overline{x}_m)(x_{ki}-\overline{x}_k)$

为了表示这d个随机变量两两间的相关关系，提出了协方差矩阵的概念，协方差矩阵形式如下：

$\Sigma=\begin{bmatrix}\sigma(x_1,x_1)&\sigma(x_1,x_2)&\dots&\sigma(x_1,x_n)\\\sigma(x_2,x_1)&\sigma(x_2,x_2)&\dots&\sigma(x_2,x_n)\\\vdots&\vdots&\ddots&\vdots\\\sigma(x_n,x_1)&\sigma(x_n,x_2)&\dots&\sigma(x_n,x_n)\end{bmatrix}\in R^{d\times d}$

其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，根据协方差的定义，我们可以知道协方差矩阵是一个对称矩阵。

1.2 多元正态分布与线性变换

假设一个向量 $x$服从均值向量为 $\mu$、协方差矩阵为 $\Sigma$的多元正态分布，则：

$p(x)={1\over\sqrt{2\pi\Sigma}}e^{-{1\over2}(x-\mu)^T\Sigma^{-1}(x-\mu)}$

令该分布的均值向量为 $\mu=0$，由于指数项外面的系数 $|2\pi\Sigma|^{-{1\over2}}$通常是常数，故可将多元正态分布简化为

$p(x)\varpropto exp(-{1\over2}x^T\Sigma^{-1}x)$

此时用二元正态分布实例化这个分布，令 $x=(y,z)^T$，包含两个随机变量 $y$和 $z$，则协方差矩阵可写成如下形式：

$\Sigma=\begin{bmatrix}\sigma(y,y)&\sigma(y,z)\\\sigma(z,y)&\sigma(z,z)\end{bmatrix}\in R^{2\times2}$

假设这个协方差矩阵为单位矩阵，生成若干个随机数如下图所示：

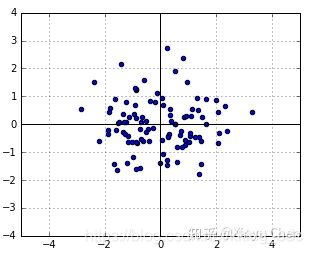
在生成的若干个随机数中，每个点的似然为：

$L(x)\varpropto exp(-{1\over2}x^Tx)$

对上图中的每个点都考虑一步线性变换： $t=A(x)$，我们可以得到图二：