数据结构堆的概念&&堆排序的思想以及算法过程详解（图文）

一、堆的概念

介绍堆之前，首先来看二叉树 Binary Tree。

二叉树是树的一种，主要的特点是二叉树的所有节点最多只有两个叶节点。除此之外没有别的要求。

Complete Binary Tree(完全二叉树): 二叉树的一种。在完全二叉树当中，除了最后一层之外，所有层的节点都是满的，且最后一层的节点也是从左到右的。优先填满左边的节点。
Full Binary Tree(满二叉树): 二叉树的一种。满二叉树的所有层，包括最后一层，都是满的。也就是说，除了最后一层的节点外所有的节点都有两个子节点。

这两者之间的关系：完全二叉树是从满二叉树里引出的。满二叉树最下一层的子节点，如果是从右往左拿掉，不论多少，剩下的都是完全二叉树，如果不是从右往左拿，而是在中间拿掉了一个，就不是完全二叉树了。

满二叉树和完全二叉树如下图示例：
在这里插入图片描述

很容易理解吧！

然后再看 堆 Heap 的定义。

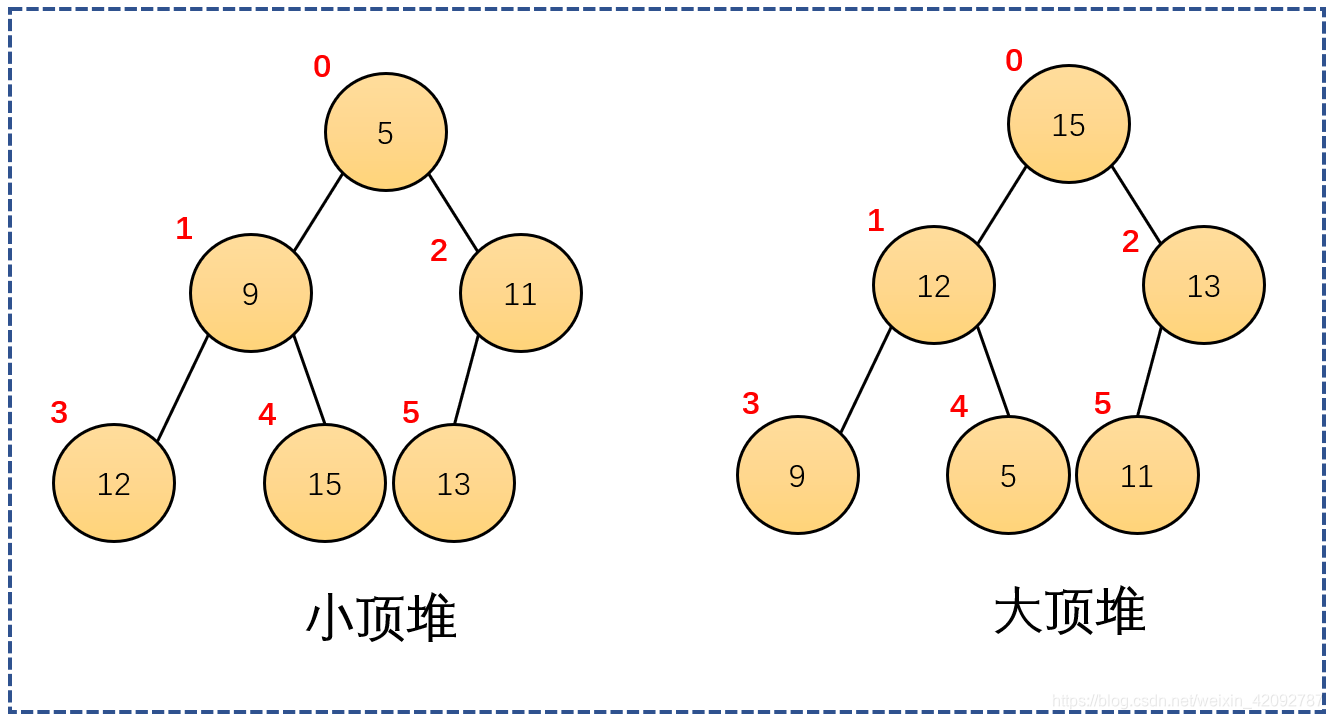
Heap(堆): 堆是一种完全二叉树。在树的性质之外，堆要求节点按照大小（父节点比子节点大/父节点比子节点小）来排列。除完全二叉树的性质外，他还要求堆内元素按照某种固定的大小顺序排列。

Min Heap(最小堆): 最小的键值总是在最前面。换句话说，所有的父节点都比他们的子节点小。
Max Heap(最大堆): 最大的键值总是在最前面。换句话说，所有的父节点都比他们的子节点大。

最小堆也叫小顶堆，小根堆；最大堆也叫大顶堆，大根堆。

那么我们填入数字，对最小堆、最大堆，做一个示例：
在这里插入图片描述

二、堆的存储和堆排序思想

2.1 堆存储

堆在逻辑上就是树，因此存储的方式也可以是链表，不过按照这种存储，需要数据本身，以及节点之间的关系指针，耗费空间比较大。

由于堆是完全二叉树，除了最下面的一层，其余层都是满的，那么每层的节点个数就一定是 1、2、4、8、……、2^^n-1-x（最后一层可满可不满）

他们之间的下标关系很明确，因此一般用数组存储，访问起来也很方便。

下图是对于上面示例的小顶堆和大顶堆的对应数组存储示意。

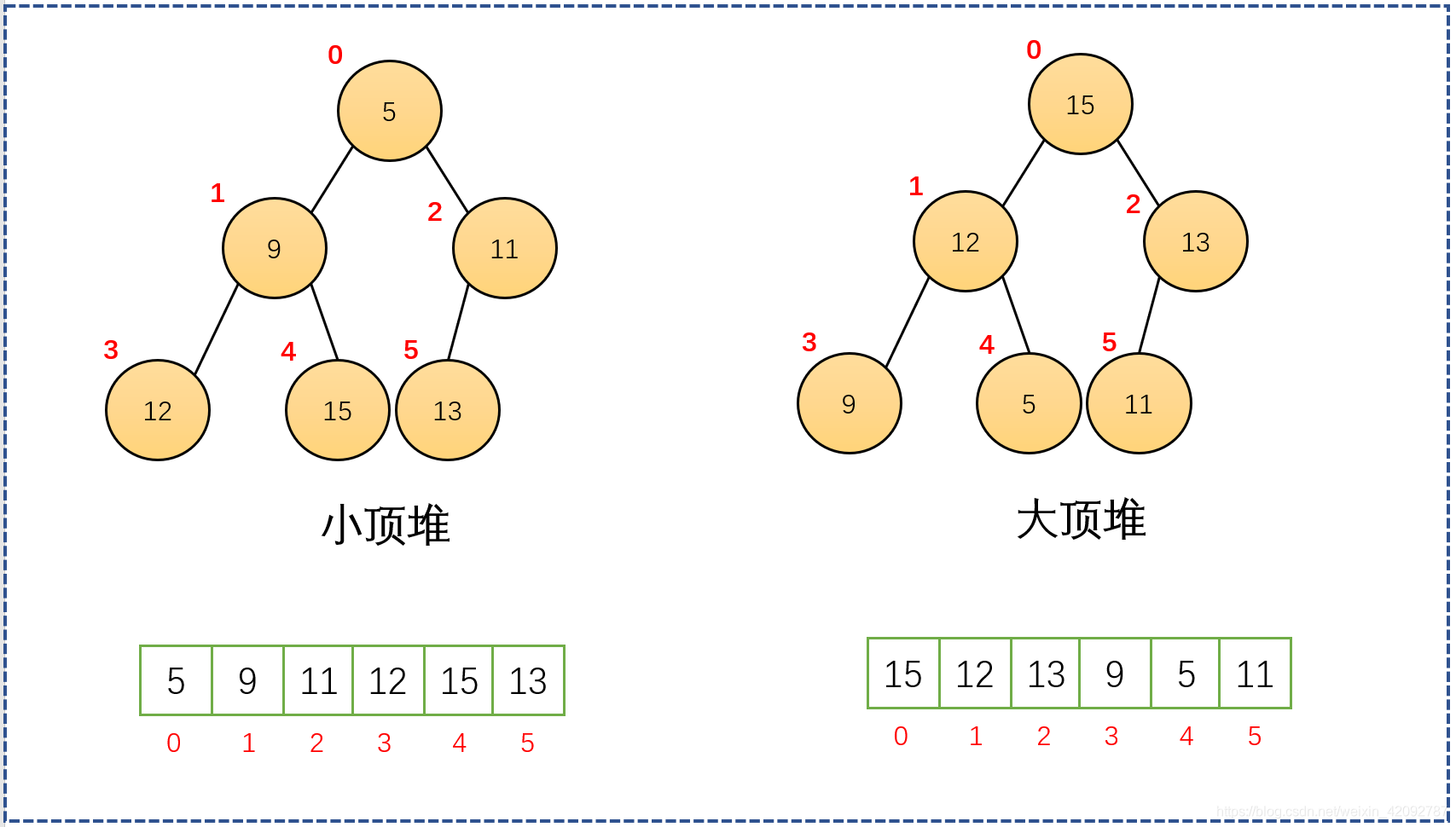
在这里插入图片描述

可以看到，对于小顶堆的性质，可以直接用数组之间的下标关系表示成为：

arr[ i ] <= arr[ 2 i + 1 ] && arr[ i ] <= arr[ 2i + 2 ]

同理，大顶堆：

arr[ i ] >= arr[ 2i + 1 ] && arr[ i ] >= arr[ 2i + 2 ]

也就是任意一个子树的父节点都小于等于（大于等于）他们的左右子节点，前提是存在。

可以看到，堆的性质本身带有递归的特性：
对于根节点来说，子树的节点大小都大于（小于）他；
对于左右子树，同样有他们的子树的节点大小都大于（小于）他；
……

这种大小关系很明确的数据结构的应用，最经常就是堆排序。

2.2 堆排序

堆排序的思想，以构造大顶堆为例：

将长度为 n 的待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换，此时末尾就为最大值。
然后将剩余 n-1 个元素重新构造成一个大顶堆，这样会得到 n 个元素的次小值，如此反复执行，便能得到一个有序序列了。

说白了，就是依次构建大顶堆，这样就能拿出一个一个的当前最大值，最后得到有序序列。

这个过程具体实现起来有一些问题需要解决。

1.输入无序，第一步先要构建出大顶堆

由于输入没有顺序的，我们先要构建出大顶堆来，才能弹出第一个最大的数。

示例输入是：[ 5 9 12 11 15 13 ]，组成了一个完全二叉树（逻辑上）

在这里插入图片描述
接着，要将他构建成一个大顶堆，就是要从最后一个非叶子节点开始从下往上，依次调整成大顶堆。

什么意思呢，比如这个例子，最后一个非叶子节点是 12 ，调整成大顶堆，就是保证 12 为根的这棵子树成为一个 子大顶堆（好像没有子大顶堆这种说法，但意思能懂吧）。然后依次操作 9、5。

调整的过程是一个递归的过程，整个流程如下图所示。

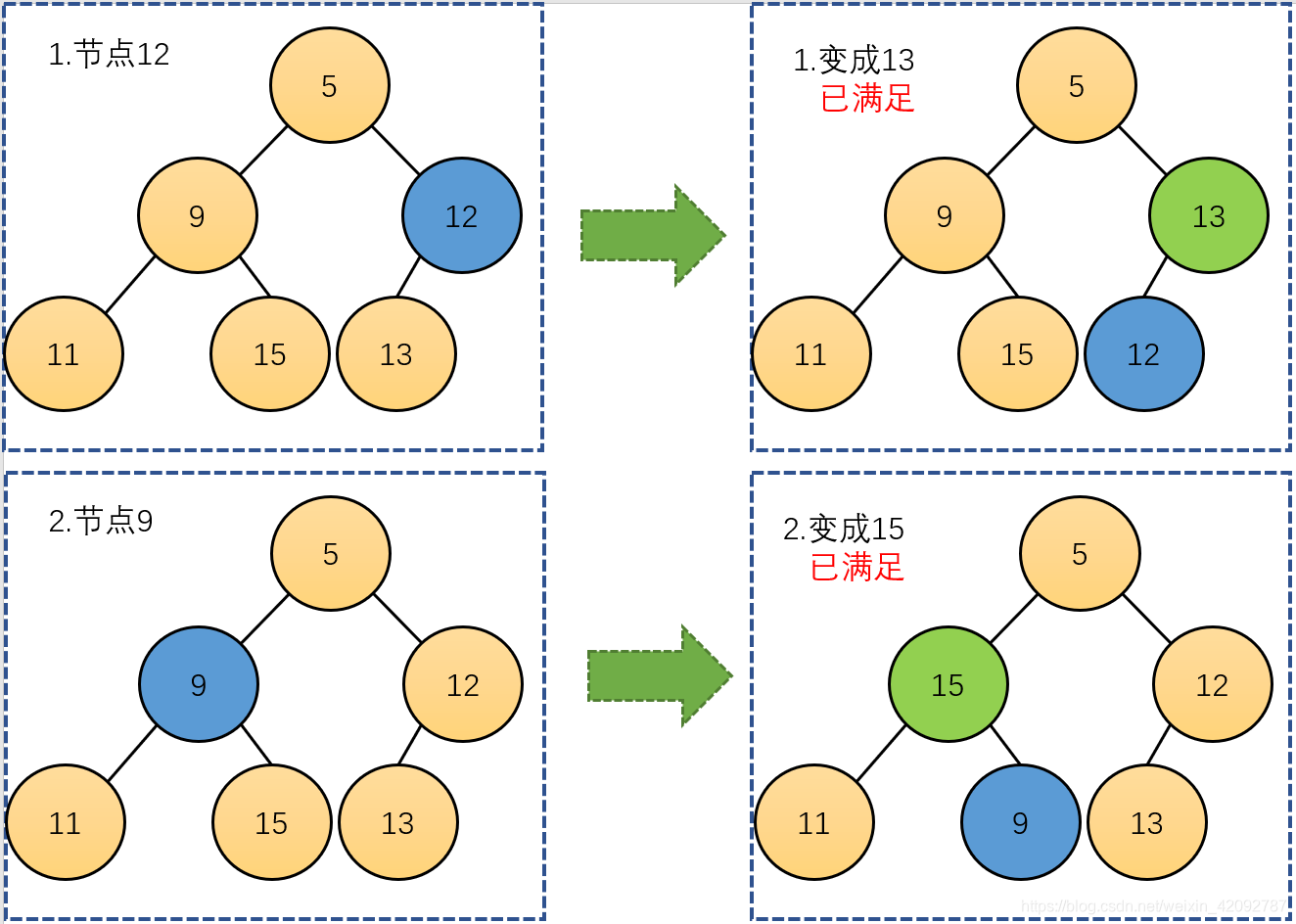
在这里插入图片描述

也就是说，从后往前，依次遍历非叶子节点，对于每一个非叶子节点，进行 “ 维护大顶堆性质 ” 的操作，而 “ 维护大顶堆性质 ” 的操作是递归进行的。

比如在上图中，往前遍历到根节点 5 ，进行维护（与子节点交换）之后，他的子树又不满足了，所以 递归向下还要进行“维护大顶堆性质”。

从后往前进行，又从前往后递归，这样不麻烦吗？一开始我有这个疑问.

后来仔细想一想：整个第一次构建大顶堆的过程只能从后往前。
否则，当从根部开始，每一次交换到根部的只是当前的最大值，而递归向下只会和后面的节点进行比较，这样在后面遇到真正的最大值，就无法正确将其放到根位置了。

相反，从后往前进行，保证了最后放到根位置的元素一定是整个序列中最大的元素。

当第一次将初始序列构建成大顶堆之后，就可以得到最大的元素，将他和最后一个叶子节点交换，此时序列的最后一个元素就是最大值。如下图所示的 15 .

在这里插入图片描述

此时，对于前 n - 1 个元素，显然不再满足大根堆的性质了，想要继续寻找剩下节点里的最大值，就要再次调用 “维护大顶堆性质” 的操作，而这一次，直接对根节点调用就可以。

这是因为，初始创建好的大根堆，从根节点到叶子节点，按层已经是越来越大的顺序，此时只要调用 “ 维护大顶堆性质 ” 操作，就会从第二层得到次大的节点，在这个操作递归向下的时候，会继续完成的子树的性质维护。

然后第三大、第四大……直到结束，就可以得到想要的排序序列。

2.每挑出一个最大元素怎么操作？

答：由于数组的元素无法删除，所以采用的方式是把每一个最大值选出来之后，和最后一个元素交换，然后将前面 n - 1 个元素继续构造；

3.剩余 n -1 个元素重新调整成大顶堆

答：这是算法的核心步骤，维护大顶堆的性质，前面已经提到：在构建初始大顶堆的时候被从后往前的每一个非叶子节点调用；在每一次弹出最大值之后对根节点再次进行调用；且这个方法是递归实现的。

我们来看过程。

仍然是上面的例子，对于第一次弹出最大值 15 之后，就要继续对于被交换后的根节点 12 调用此过程。

在这里插入图片描述

12 在交换后，到了新的位置，此时要对这个新位置递归调用 “ 维护大顶堆的性质 ” ，这个例子到这一步由于 12 已经满足，所以不用进行。

但是在前面第一次构建的时候，节点 5 的例子已经说明了这个向下递归的过程，所以也就不再重复。

三、堆排序实现

基于上面的原理分析，我们可以实现一个堆排序的代码。

1.主方法。

输入是一个数组（乱序），输出是一个从小到大有序的数组，利用大根堆来构造。

第一步，把输入数组 nums 构造成大根堆；
第二步，对于 0 到最后一个元素，先交换，再从 0 到 n-1 个元素进行维护大根堆的性质。

可以写出主方法里的如下代码：

/*
  堆排序主方法，输入int数组，进行排序
*/
public void heapSort(int[] nums){
    int size=nums.length;
    int curSize=size;
    buildMaxHeap( nums, size);

    //每一次根元素都和当前的最后一个叶子节点交换，并维护大根堆性质
    for(int i=size-1 ; i>=0 ; i--){
        swap(nums , 0 , i );
        curSize--;
        defendMaxHeap(nums , 0 , curSize);
    }
}

显然，第一次构建的 buildMaxHeap 方法需要我们实现，按照我的设计，输入当前数组，和数组的总量 size ，构建出大根堆。

2.buildMaxHeap方法

buildMaxHeap 方法的步骤：

找到最后一个非叶子节点；
调用维护大根堆性质的方法，进行维护；
依次往前退到别的非叶子节点，直到根节点。

//第一次创建大根堆
public void buildMaxHeap(int[] nums, int size){
    for(int i=size/2 ; i>=0 ;i--){
        defendMaxHeap(nums , i ,size);
    }
}

第一个初始位置是 i = size/2 ，这点很好理解，这是由于堆是完全二叉树，不需要精确到那个节点，而是大概定位到 size/2 ，在调用维护方法的过程，进一步处理。

3.defendMaxHeap方法

我们已经说过，这是一个递归方法，步骤如下：

对于当前的 i 位置节点，比较他的左右子节点，比他大，就进行交换；
交换之后，较小的节点已经到了新的位置，要对新的位置继续递归进行维护

显然我们需要的参数就是一个当前位置，除此之外还要一个当前的size，确保在计算左右孩子下标的时候不会越界。

public void defendMaxHeap(int[] nums,int i , int heapSize){
    int left = i*2+1;
    int right = i*2+2;
    int largest=i;//记录父、左、右中最大的那个
    if(left < heapSize && nums[left] > nums[largest]){
        largest = left;
    }
    if(right < heapSize && nums[right] > nums[largest]){
        largest = right;
    }
    //选择和谁交换周进行交换，并递归
    if(largest != i){
        swap( nums , i , largest);
        defendMaxHeap(nums , largest , heapSize);//递归
    }
}

4.swap

最后，这里面的交换都用了swap，我们把这个方法实现出来。

public void swap(int[] nums, int i, int j){
    int temp=nums[i];
    nums[i]=nums[j];
    nums[j]=temp;
}

这样我们的代码就写完了，前面四个合起来就是。

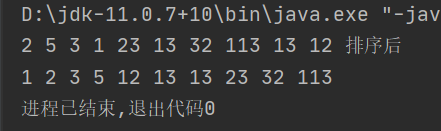
测试了一下：

在这里插入图片描述

五、总结

堆排序的主要思想是（以大根堆为例）：

首先将待排序的序列构造成堆，此时堆顶记录是堆中所有记录的最大者；
将最大者从堆中移走，一般做法是和末尾叶子节点交换；
将剩下的节点维护大顶堆的性质。

堆排序的时间复杂度：

构建初始堆经推导复杂度为O(n)；
在交换并重建堆的过程中，需交换n-1次；
对剩余维护堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)…1]逐步递减，近似为nlogn。

所以堆排序时间复杂度一般认为就是O(nlogn)级。而且，相比于快速排序的O(nlogn)，堆排序最差时间也是O(nlogn)的（快排最差达到O(n2)）。

另外，堆排序好在，如果让我们求前/第 k 大，或者前/第 k 小的时候，不用对所有元素排序，只要在过程中限制调用 “ 维护堆的性质 ” 的次数，就可以提前结束算法的运行。