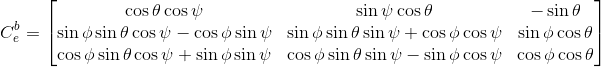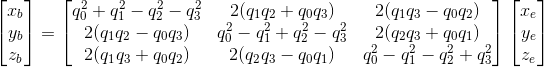pid控制器实现互补滤波原理

转载自：https://blog.csdn.net/wxc971231/article/details/97449026
https://blog.csdn.net/luoshi006/article/details/51513580

一、姿态解算原理相关

1、简介

• 对于四旋翼无人机来说，有两个相关坐标系，即地理坐标系 $OnXnYnZnO_nX_nY_nZ_nOn​Xn​Yn​Zn​$和机体坐标系 $ObXbYbZbO_bX_bY_bZ_bOb​Xb​Yb​Zb​$。
• 姿态角的检测对于四旋翼控制是至关重要的。比如在做飞行器姿态控制的时候，通常使用串级pid的方法，需要得到飞行器姿态角（即欧拉角）来做角度位置环反馈。再如利用装置在机腹垂直向下拍摄的摄像头，进行机体视觉定位时，也需要靠姿态角进行视觉反馈补偿。
• 要解算姿态角，就要研究从地理坐标系到机体坐标系的转换过程。这个转换过程不是唯一的，比如可以先绕X轴旋转 $θ\thetaθ$，再绕Y轴旋转 $γ\gammaγ$，最后绕Z轴旋转 $ψ\psiψ$，这样得到的一组姿态角称为卡尔丹角；也可以按ZYX的顺序旋转，这样得到的一组姿态角称为欧拉角（这是最常用的，pitch,roll,yaw）。不管按照什么顺序，得到的角度都可以称作广义欧拉角。实际理论分析时，旋转顺序不是很重要，这个顺序会影响四元数与欧拉角的关系，但是都可以进行解算。

2、坐标变换和旋转矩阵

下面从最基本的坐标变换入手开始讲解，请看如下坐标系旋转： $OAXAYAZAO_AX_AY_AZ_AOA​XA​YA​ZA​$绕OX旋转 $θ\thetaθ$到 $OBXBYBZBO_BX_BY_BZ_BOB​XB​YB​ZB​$

对于原系 $OAXAYAZAO_AX_AY_AZ_AOA​XA​YA​ZA​$中的一个向量 $[rxA,ryA,rzA][r_{x_A},r_{y_A},r_{z_A}][rxA​​,ryA​​,rzA​​]$，转换到新系 $OBXBYBZBO_BX_BY_BZ_BOB​XB​YB​ZB​$中的向量 $[rxB,ryB,rzB][r_{x_B},r_{y_B},r_{z_B}][rxB​​,ryB​​,rzB​​]$，有：

$rxB=rxAryB=cos(θ)ryA+sin(θ)rzArzB=−sin(θ)ryA+cos(θ)rzAr_{x_B}=r_{x_A} \\ r_{y_B}=cos(\theta)r_{y_A}+sin(\theta)r_{z_A} \\ r_{z_B}=-sin(\theta)r_{y_A}+cos(\theta)r_{z_A}rxB​​=rxA​​ryB​​=cos(θ)ryA​​+sin(θ)rzA​​rzB​​=−sin(θ)ryA​​+cos(θ)rzA​​$

可以用旋转矩阵表示

$[rxBryBrzB]=[1000cos(θ)sin(θ)0−sin(θ)cos(θ)][rxAryArzA] {\left[ \begin{array}{c} r_{x_B}\\ r_{y_B}\\ r_{z_B} \end{array} \right ]}= {\left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & cos(\theta) & sin(\theta)\\ 0 & -sin(\theta) & cos(\theta) \end{array} \right ]} {\left[ \begin{array}{c} r_{x_A}\\ r_{y_A}\\ r_{z_A} \end{array} \right ]} ⎣⎡​rxB​​ryB​​rzB​​​⎦⎤​=⎣⎡​100​0cos(θ)−sin(θ)​0sin(θ)cos(θ)​⎦⎤​⎣⎡​rxA​​ryA​​rzA​​​⎦⎤​$

• 中间的就是 绕x轴旋转 $θ\thetaθ$ 的旋转矩阵，记作
  $Cx(θ)=[1000cos(θ)sin(θ)0−sin(θ)cos(θ)] C_{x_(\theta)}= {\left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & cos(\theta) & sin(\theta)\\ 0 & -sin(\theta) & cos(\theta) \end{array} \right ]} Cx(​θ)​=⎣⎡​100​0cos(θ)−sin(θ)​0sin(θ)cos(θ)​⎦⎤​$

• 同样的，还有 绕y轴旋转 $γ\gammaγ$ 的旋转矩阵，记作
  $Cy(γ)=[cos(γ)0−sin(γ)010sin(γ)0cos(γ)] C_{y_(\gamma)}= {\left[ \begin{array}{ccc} cos(\gamma) & 0 & -sin(\gamma)\\ 0 & 1 & 0\\ sin(\gamma) & 0 & cos(\gamma) \end{array} \right ]} Cy(​γ)​=⎣⎡​cos(γ)0sin(γ)​010​−sin(γ)0cos(γ)​⎦⎤​$

• 同样的，还有 绕z轴旋转 $ψ\psiψ$ 的旋转矩阵，记作
  $Cz(ψ)=[cos(ψ)−sin(ψ)0sin(ψ)cos(ψ)0001] C_{z_(\psi)}= {\left[ \begin{array}{ccc} cos(\psi) & -sin(\psi) & 0 \\ sin(\psi) & cos(\psi) & 0 \\ 0 & 0 & 1 \end{array} \right ]} Cz(​ψ)​=⎣⎡​cos(ψ)sin(ψ)0​−sin(ψ)cos(ψ)0​001​⎦⎤​$

• 假如现在我们按ZXY的顺序，从地理坐标系 $OnXnYnZnO_nX_nY_nZ_nOn​Xn​Yn​Zn​$旋转到机体坐标系 $ObXbYbZbO_bX_bY_bZ_bOb​Xb​Yb​Zb​$，整体旋转矩阵为
  $Cnb=Cy(γ)Cx(θ)Cz(ψ)=[cos(γ)cos(ψ)+sin(γ)sin(ψ)sin(θ)−cos(γ)sin(ψ)+sin(γ)cos(ψ)cos(θ)−sin(ψ)cos(θ)sin(ψ)cos(θ)cos(ψ)cos(θ)sin(θ)sin(γ)cos(ψ)−cos(γ)sin(ψ)sin(θ)−sin(γ)sin(ψ)−cos(γ)cos(ψ)sin(θ)cos(γ)cos(θ)] C_n^b=C_{y_(\gamma)}C_{x_(\theta)}C_{z_(\psi)}= {\left[ \begin{array}{ccc} cos(\gamma)cos(\psi)+ sin(\gamma)sin(\psi)sin(\theta) & -cos(\gamma)sin(\psi)+sin(\gamma)cos(\psi)cos(\theta) & -sin(\psi)cos(\theta) \\ sin(\psi)cos(\theta)& cos(\psi)cos(\theta) & sin(\theta) \\ sin(\gamma)cos(\psi)- cos(\gamma)sin(\psi)sin(\theta) & -sin(\gamma)s in(\psi)-cos(\gamma)cos(\psi)sin(\theta) & cos(\gamma)cos(\theta) \end{array} \right ]} Cnb​=Cy(​γ)​Cx(​θ)​Cz(​ψ)​=⎣⎡​cos(γ)cos(ψ)+sin(γ)sin(ψ)sin(θ)sin(ψ)cos(θ)sin(γ)cos(ψ)−cos(γ)sin(ψ)sin(θ)​−cos(γ)sin(ψ)+sin(γ)cos(ψ)cos(θ)cos(ψ)cos(θ)−sin(γ)sin(ψ)−cos(γ)cos(ψ)sin(θ)​−sin(ψ)cos(θ)sin(θ)cos(γ)cos(θ)​⎦⎤​$

• 注意一点，如果从n系到b系的旋转矩阵为 $CnbC_n^bCnb​$，则从b系到n系的旋转矩阵为 $CnbT{C_n^b}^TCnb​T$，显然有 $Cnb∗CnbT=EC_n^b*{C_n^b}^T=ECnb​∗Cnb​T=E$，所以旋转矩阵是正交矩阵

• 这个结论不能直接使用，一方面这个直接是不可解的，另一方面大量三角函数运算会导致大量资源占用。

3、四元数

• 四元数是一种超复数，由四个元构成： $Q(q0,q1,q2,q3)=q0+q1i+q2i+q3kQ(q_0,q_1,q_2,q_3)=q_0+q_1i+q_2i+q_3kQ(q0​,q1​,q2​,q3​)=q0​+q1​i+q2​i+q3​k$
• 关于四元数更详细的介绍可以参考四元数
• 利用四元数我们可以提出另一种描述空间矩阵的方法，具体可以参考秦永元的《惯性导航》和【教程】四旋翼飞行器姿态解算算法入门学习-Rick Grimes

（1）四元数和欧拉角的关系

• 注意这三个式子中， $θ\thetaθ$是绕Y轴转角， $ϕ\phiϕ$是绕X轴转角， $ψ\psiψ$是绕Z轴转角，和前文有所不同

1. 按ZYX的顺序从地理坐标系 $OeXeYeZeO_eX_eY_eZ_eOe​Xe​Ye​Ze​$旋转到机体坐标系 $ObXbYbZbO_bX_bY_bZ_bOb​Xb​Yb​Zb​$，整体旋转矩阵为
   
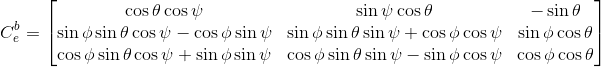
2. 对应的四元数表示法为：
   
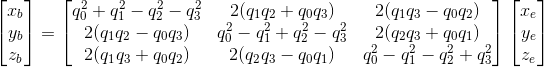
3. 解算出的欧拉角为
   

（2）四元数的求解

• 飞行器姿态的改变，可以对应到旋转矩阵的改变，进一步对应到四元数的改变。实时姿态计算，实际上也就是实时更新四元数。
• 我们可以构建四元数关于时间的微分方程，来研究四元数关于时间的变化规律，求解该微分方程，即可解出四元数

1、建立微分方程

• 从四元数的三角表示法入手推到微分方程，具体推到过程可以参考秦永元的《惯性导航》
  $Q=cos(θ)2+λsin(θ)2Q=\frac{cos(\theta)}{2}+\frac{\lambda sin(\theta)}{2} Q=2cos(θ)​+2λsin(θ)​$ $dQdt=1/2[0−ωx−ωy−ωxωx0ωz−ωyωy−ωz0ωxωzωy−ωx0]⋅[q0q1q2q3] \frac{dQ}{dt}=1/2 {\left[ \begin{array}{cccc} 0 & -\omega_x & -\omega_y & -\omega_x\\ \omega_x & 0 & \omega_z & -\omega_y\\ \omega_y & -\omega_z & 0 & \omega_x\\ \omega_z & \omega_y & -\omega_x & 0 \end{array} \right ]}· {\left[ \begin{array}{c} q_0\\ q_1\\ q_2\\ q_3 \end{array} \right ]} dtdQ​=1/2⎣⎢⎢⎡​0ωx​ωy​ωz​​−ωx​0−ωz​ωy​​−ωy​ωz​0−ωx​​−ωx​−ωy​ωx​0​⎦⎥⎥⎤​⋅⎣⎢⎢⎡​q0​q1​q2​q3​​⎦⎥⎥⎤​$ $记为dQdt=Φ⋅Q 记为 \frac{dQ}{dt}=\Phi·Q 记为dtdQ​=Φ⋅Q$

2、一阶龙格库塔法求解微分方程

一阶龙格库塔法是求解微分方程常用的工程方法，原理是把微分转化为微元增量，利用递推迭代的方法求解

• 设有微分方程 $dydx=f(x,y)\frac{dy}{dx}=f(x,y)dxdy​=f(x,y)$

  求解y的迭代公式为 $y(λ+Δλ)=y(λ)+Δλ⋅f(x(λ),y(λ))y(\lambda+\Delta\lambda)=y(\lambda)+\Delta\lambda·f(x(\lambda),y(\lambda))y(λ+Δλ)=y(λ)+Δλ⋅f(x(λ),y(λ))$

• 对应到四元数微分方程：
  $Q(t−Δt)=Q(t)+Δt⋅Φ(t)⋅Q(t) Q(t-\Delta t)=Q(t)+\Delta t·\Phi(t)·Q(t) Q(t−Δt)=Q(t)+Δt⋅Φ(t)⋅Q(t)$
  整理得
  $[q0q1q2q3]t+Δt=[q0q1q2q3]t+12⋅Δt⋅[−ωx⋅q1−ωy⋅q2−ωz⋅q3ωx⋅q0−ωy⋅q3+ωz⋅q2ωx⋅q3+ωy⋅q0−ωz⋅q1−ωx⋅q2+ωy⋅q1+ωz⋅q0] {\left[ \begin{array}{c} q_0\\ q_1\\ q_2\\ q_3 \end{array} \right ]}_{t+\Delta t}= {\left[ \begin{array}{c} q_0\\ q_1\\ q_2\\ q_3 \end{array} \right ]}_{t}+ \frac{1}{2}· \Delta t· {\left[ \begin{array}{c} -\omega_x·q_1 -\omega_y·q_2 -\omega_z ·q_3\\ \omega_x·q_0 -\omega_y·q_3 +\omega_z ·q_2\\ \omega_x·q_3 +\omega_y·q_0 -\omega_z ·q_1\\ -\omega_x·q_2 +\omega_y·q_1 +\omega_z ·q_0 \end{array} \right ]} ⎣⎢⎢⎡​q0​q1​q2​q3​​⎦⎥⎥⎤​t+Δt​=⎣⎢⎢⎡​q0​q1​q2​q3​​⎦⎥⎥⎤​t​+21​⋅Δt⋅⎣⎢⎢⎡​−ωx​⋅q1​−ωy​⋅q2​−ωz​⋅q3​ωx​⋅q0​−ωy​⋅q3​+ωz​⋅q2​ωx​⋅q3​+ωy​⋅q0​−ωz​⋅q1​−ωx​⋅q2​+ωy​⋅q1​+ωz​⋅q0​​⎦⎥⎥⎤​$
  这里 $ω\omegaω$就是三轴角速度，可以用陀螺仪直接测得

4、旋转矩阵中的一列

• 旋转矩阵中的一列有特殊意义，它代表原坐标系中一个方向的单位向量（X/Y/Z），在新坐标系中对应的向量值
• 用方向向量（如X方向 $[1,0,0]T[1,0,0]^T[1,0,0]T$）左乘旋转矩阵可以轻易看出，这里不写了

二、匿名四轴姿态解算分析

按Ano_Imu.c文件顺序进行分析

1、坐标系定义

• 匿名四轴姿态解算部分主要写在Ano_Imu.c中
• 匿名四轴程序中一共有三个坐标系：

1. 地理坐标系，标记为w（官方定义如下）
2. 机体坐标系，标记为a（官方定义如下）
   
3. 航向坐标系，标记为h（专门解释一下，四旋翼飞行时，姿态角pitch和roll一般很小，在任意时刻，如果我们粗略地认为飞行器始终与底面平行（把飞机摆正，使pitch=roll=0），此时的机体坐标系即为航向坐标系）

2、坐标系转换

（1）匿名旋转坐标系

• 匿名的坐标系变换，是按是按ZYX顺序从地理坐标系转到机体坐标系的，这个旋转矩阵是前面提过的 (注意这三个式子中， $θ\thetaθ$是绕Y轴转角， $ϕ\phiϕ$是绕X轴转角， $ψ\psiψ$是绕Z轴转角)

$Cwa=[cos(θ)cos(ψ)sin(ψ)cos(θ)−sin(θ)sin(ϕ)sin(θ)cos(ψ)−cos(ϕ)sin(ψ)sin(ϕ)sin(θ)sin(ψ)+cos(ϕ)cos(ψ)sin(ϕ)cos(θ)cos(ϕ)sin(θ)cos(ψ)+sin(ϕ)sin(ψ)cos(ϕ)sin(θ)sin(ψ)−sin(ϕ)cos(ψ)cos(ϕ)cos(θ)] C_w^a= {\left[ \begin{array}{ccc} cos(\theta)cos(\psi) & sin(\psi)cos(\theta) & -sin(\theta) \\ sin(\phi)sin(\theta)cos(\psi)- cos(\phi)sin(\psi) & sin(\phi)sin(\theta)sin(\psi)+cos(\phi)cos(\psi) & sin(\phi)cos(\theta) \\ cos(\phi)sin(\theta)cos(\psi)+ sin(\phi)sin(\psi) & cos(\phi)sin(\theta)sin(\psi)-sin(\phi)cos(\psi) & cos(\phi)cos(\theta) \end{array} \right ]} Cwa​=⎣⎡​cos(θ)cos(ψ)sin(ϕ)sin(θ)cos(ψ)−cos(ϕ)sin(ψ)cos(ϕ)sin(θ)cos(ψ)+sin(ϕ)sin(ψ)​sin(ψ)cos(θ)sin(ϕ)sin(θ)sin(ψ)+cos(ϕ)cos(ψ)cos(ϕ)sin(θ)sin(ψ)−sin(ϕ)cos(ψ)​−sin(θ)sin(ϕ)cos(θ)cos(ϕ)cos(θ)​⎦⎤​$

• 程序中用二维数组att_matrix表示从机体坐标系转到地理坐标系的旋转矩阵，是上面那个的转置
  $att_matrix=Caw=(Cwa)T=[cos(θ)cos(ψ)sin(ϕ)sin(θ)cos(ψ)−cos(ϕ)sin(ψ)cos(ϕ)sin(θ)cos(ψ)+sin(ϕ)sin(ψ)sin(ψ)cos(θ)sin(ϕ)sin(θ)sin(ψ)+cos(ϕ)cos(ψ)cos(ϕ)sin(θ)sin(ψ)−sin(ϕ)cos(ψ)−sin(θ)sin(ϕ)cos(θ)cos(ϕ)cos(θ)] att\_matrix=C_a^w=(C_w^a)^T= {\left[ \begin{array}{ccc} cos(\theta)cos(\psi) & sin(\phi)sin(\theta)cos(\psi)- cos(\phi)sin(\psi) &cos(\phi)sin(\theta)cos(\psi)+ sin(\phi)sin(\psi) \\ sin(\psi)cos(\theta) &sin(\phi)sin(\theta)sin(\psi)+cos(\phi)cos(\psi) & cos(\phi)sin(\theta)sin(\psi)-sin(\phi)cos(\psi) \\ -sin(\theta) &sin(\phi)cos(\theta) & cos(\phi)cos(\theta) \end{array} \right ]} att_matrix=Caw​=(Cwa​)T=⎣⎡​cos(θ)cos(ψ)sin(ψ)cos(θ)−sin(θ)​sin(ϕ)sin(θ)cos(ψ)−cos(ϕ)sin(ψ)sin(ϕ)sin(θ)sin(ψ)+cos(ϕ)cos(ψ)sin(ϕ)cos(θ)​cos(ϕ)sin(θ)cos(ψ)+sin(ϕ)sin(ψ)cos(ϕ)sin(θ)sin(ψ)−sin(ϕ)cos(ψ)cos(ϕ)cos(θ)​⎦⎤​$
• 注意这里绕Y轴转角 $θ\thetaθ$ (pitch)，绕X轴转角 $ϕ\phiϕ$ (roll)都是很小的角

（2）相关代码分析

#