(2) 李航《统计学习方法》基于Python实现——感知机

一：概述

感知机（perceptron）是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1两类。感知机对应于输入空间（特征空间）中将实例划分为正负两类的超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。

感知机学习算法分为原始形式和对偶形式，由Rosenblatt在1957年提出，是神经网络和支持向量机的基础。

相关概念：

监督学习的任务就是学习一个模型，应用这个模型，对给定的输入预测相应的输出。这个模型的一般形式为决策函数： $Y=f(X)$ ，或者条件概率分布： $P(Y | X)$
监督学方法又可以分为生成方法和判别方法，所学到的模型又分别称为生成模型和判别模型。
- 1：生成方法由数据学习联合概率分布 $P(X, Y)$ ，然后求出条件概率分布 $P(Y | X)$ 作为预测的模型，即生成模型： $P(Y | X)=\frac{P(X, Y)}{P(X)}$
  这样的方法之所以称为生成方法，是因为模型表示了给定输入X，产生输出Y的生成关系。典型的生成模型有：朴素贝叶斯和隐马尔科夫模型。
- 2：判别方法由数据直接学习决策函数 $f(X)$ 或者条件概率 $P(Y | X)$ 作为预测的模型，即判别模型，判别方法关心的是对给定的输入X，应该预测什么样的输出Y。典型的判别模型包括： $k$ 近邻法，感知机，决策树，逻辑回归，最大熵模型，支持向量机，提升方法和条件随机场等。

二：感知机学习策略

在引入感知机学习策略之前，首先介绍数据集的线性可分性：

假设给定一个数据集： $T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$ ，其中， $x_{i} \in \mathcal{X}=\mathbf{R}^{n}, \quad y_{i} \in \mathcal{Y}=\{+1,-1\}, \quad i=1,2, \cdots, N$
如果存在某个超平面： $w \cdot x+b=0$ ，能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有 $y_{i}=+1$ 的实例 $i$ ，有 $w \cdot x_{i}+b>0$ ，对所有 $y_{i}=-1$ 的实例 $i$ ，有 $w \cdot x_{i}+b<0$ ，则称数据集 $T$ 是线性可分的，否则就不是线性可分。

因此，如果我们进一步假设训练数据是线性可分的，那么感知机的目标就是找到能够将正负实例点完全分开的超平面，也就是求得的超平面的参数 $w ,b$ 。这就需要用到学习策略！

大多数的机器学习模型训练过程：需要首先找到损失函数，然后转化为最优化问题，用梯度下降等方法进行更新参数，按照这个逻辑最终学习到我们模型的参数w，b。

但是不幸的是，这样的损失函数并不是w，b连续可导（无法用函数形式来表达出误分类点的个数），无法进行优化。于是我们想转为另一种选择，误分类点到超平面的总距离（直观来看，总距离越小越好）。

首先，输入空间 $\mathbf{R}^{n}$ 中任一点 $x_{0}$ 到超平面 $S$ 的距离： $\frac{1}{\|w\|}\left|w \cdot x_{0}+b\right|$ ，这里 $\|w\|$ 是 $W$ 的 $L_{2}$ 范数。

其次对于误分类点来说，由于 $w \cdot x_{i}+b$ 经过sign函数后的结果与其类别（-1或+1）不相等，所以 $y_{i}\left(w \cdot x_{i}+b\right)<0$ ，我们再转换一下： $-y_{i}\left(w \cdot x_{i}+b\right)>0$

所以误分类点到超平面的距离为： $-\frac{1}{\|w\|} y_{i}\left(w \cdot x_{i}+b\right)$ ，这样假设超平面 $S$ 的误分类集合为 $M$

那么所有误分类点到超平面 $S$ 的总距离为： $-\frac{1}{\|w\|} \sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right)$

不考虑 $\frac{1}{\|w\|}$ ，就得到感知机的损失函数： $L(w, b)=-\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right)$

问题：就是为什么可以不考虑 $\frac{1}{\|w\|}$ ，不用总距离表达式作为损失函数呢？

===> 感知机的任务是进行二分类工作，它最终并不关心得到的超平面离各点的距离有多少（所以我们最后才可以不考虑 $\frac{1}{\|w\|}$ ），只是关心我最后是否已经正确分类正确（也就是考虑误分类点的个数），比如说下面红色与绿线，对于感知机来说，效果任务是一样好的。
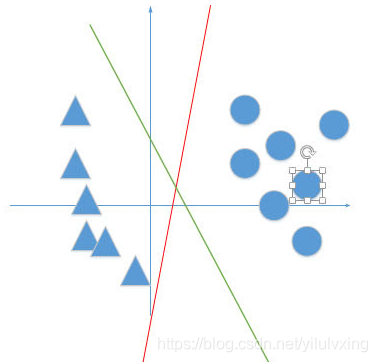
在这里插入图片描述
注意：在SVM的评价标准中（绿线是要比红线好的

三：感知机学习算法的原始形式

以上，我们知道感知机学习算法由误分类驱动的，具体采用随机梯度下降方法。首先，任意选取一个超平面 $w_{0}, b_{0}$ ，然后用梯度下降不断地极小化目标函数，极小化过程中不是一次使 $M$ 中所有误分类的梯度下降，而是一次随机选取一个误分类点使其下降。

假设误分类点集合 $M$ 是固定的，那么损失函数 $L(w, b)$ 的梯度由：
$\nabla_{w} L(w, b)=-\sum_{x_{i} \in M} y_{i} x_{i}$ 和 $\nabla_{b} L(w, b)=-\sum_{x_{i} \in M} y_{i}$ 给出。

随机选取一个误分类点 $\left(x_{i}, y_{i}\right)$ ，对 $w, b$ 进行更新：
$w \leftarrow w+\eta y_{i} x_{i}$ ， $b \leftarrow b+\eta y_{i}$ ，式中 $\eta(0<\eta \leqslant 1)$ 是步长，在感知机中成为学习率。这样可以期望损失函数 $L(w, b)$ 不断减小，直到为0，求得最后的参数 $w,b$ 的结果。

四：Python 实现感知机

基于Python实现的感知机

代码：

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# 导入数据
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label'] = iris.target

# 选择其中的4个特征进行训练
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']

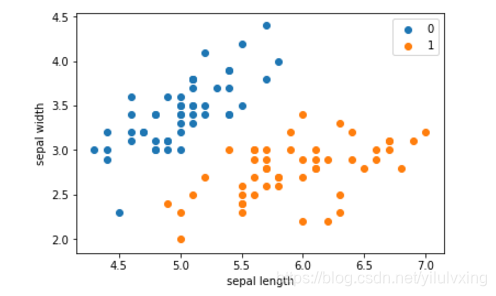
plt.scatter(df[:50]['sepal length'],df[:50]['sepal width'],label='0')
plt.scatter(df[50:100]['sepal length'],df[50:100]['sepal width'],label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

原始数据集筛选特征后的分布结果：
在这里插入图片描述

感知机构造

# 取前100条数据，为了方便展示，取2个特征
# 首先数据类型转换，为了后面的数学计算
data = np.array(df.iloc[:100, [0, 1, -1]])

X, y = data[:,:-1], data[:,-1]

y = np.array([1 if i == 1 else -1 for i in y])

class Model():
    def __init__(self):
        self.w = np.ones(len(data[0])-1,dtype=np.float32)
        self.b = 0
        self.l_rate =0.1
    
    def sign(self,x,w,b):
        y = np.dot(x,w) + b
        return y
    
    # 选择随机梯度下降方法进行拟合
    def fit(self,X_train,y_train):
        is_wrong =False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X,self.w,self.b) <= 0:
                    self.w = self.w +self.l_rate * np.dot(y,X)
                    self.b = self.b + self.l_rate *y 
                    wrong_count += 1
               
            if wrong_count ==0:
                is_wrong = True
        return 'Perceptron Model!'
    
    def score(self):
        pass
    
# 拟合
perceptron = Model()
perceptron.fit(X,y)

# 画出图形
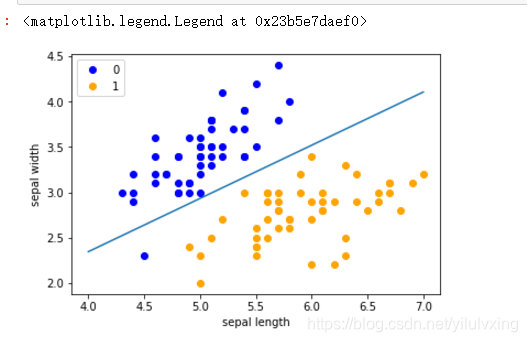
x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

运行结果
在这里插入图片描述

五运用sklean直接构造感知机

from sklearn.linear_model import Perceptron
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
clf.fit(X, y)

# Weights assigned to the features.
print(clf.coef_)

# 截距 Constants in decision function.
print(clf.intercept_)

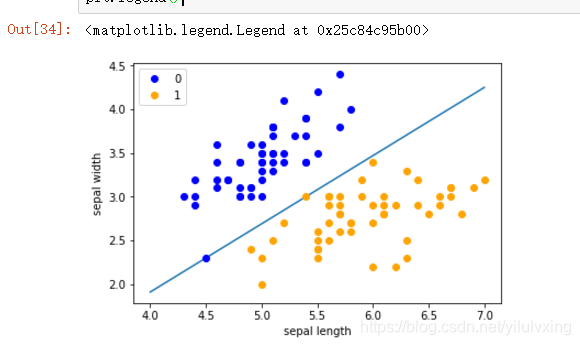
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

运行结果
在这里插入图片描述