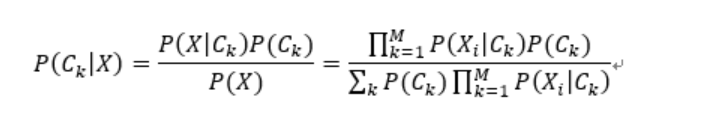朴素贝叶斯 & n-gram模型

1. 朴素朴素贝叶斯模型

1.1 贝叶斯公式

上图中P(X)是全概率公式：

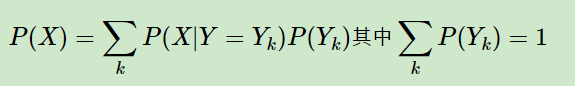
1.2 贝叶斯模型理论

我们以垃圾邮件分类为例，输入是文本X，比如“我司可办理正规发票”，输出是Y，即是否是垃圾邮件，由X得到Y的模型就是计算P(Y|X)，如果该概率大于0.5，那么就是垃圾邮件。数学表达式如下：
$$P(Y=“垃圾邮件”|X=“我司可办理正规发票”)；当该值大于0.5时，判断为垃圾邮件，否则不是垃圾邮件$$
计算公式如下：
$$P(Y=“垃圾邮件”|X=“我司可办理正规发票”)=\frac{count(“我司可办理正规发票”)}{垃圾邮件中出现X的次数+正常邮件中出现X的次数}$$
但是实际中，训练集是有限的，而句子的可能性则是无限的。所以覆盖所有句子可能性的训练集是不存在的。但是词语就那么些，因此要先分词。由此上述公式变为：
$$P(Y=“垃圾邮件”|X=“我司可办理正规发票”)=P(Y=“垃圾邮件”|(“我”,“司”,“可”,“办理”,“正规发票”))=\frac{P(“我”,“司”,“可”,“办理”,“正规发票”|“垃圾邮件”)P(“垃圾邮件”)}{P(“我”,“司”,“可”,“办理”,“正规发票”)}$$

1.3 朴素贝叶斯模型

• 随机变量的独立性：两个随机变量X和Y，若对于所有x，y有P(X=x，Y=y)=P(X=x)P(Y=y)则称随机变量和是相互独立的，记作X⊥Y。
• 条件独立：如果关于X和Y的条件概率对于Z的每一个值有P(X=x，Y=y|Z=z)=P(X=x|Z=z)P(Y=y|Z=z)，则称随机变量X和Y在给定随机变量Z时是条件独立的，记作X⊥Y|Z。
  为什么朴素贝叶斯模型有朴素二字呢？朴素在哪里？朴素贝叶斯在贝叶斯理论基础上有一条条件独立的假设，因此叫“朴素”。
  由此，第二章，朴素贝叶斯的公式
  $$P(Y=“垃圾邮件”|X=“我司可办理正规发票”)=P(Y=“垃圾邮件”|(“我”,“司”,“可”,“办理”,“正规发票”))=\frac{P(“我”,“司”,“可”,“办理”,“正规发票”|“垃圾邮件”)P(“垃圾邮件”)}{P(“我”,“司”,“可”,“办理”,“正规发票”)}$$
  将变为以下：
  $$P(Y=“垃圾邮件”|X=“我司可办理正规发票”)=\frac{{\sum }_{k}P(k|“垃圾邮件”)P(“垃圾邮件”)}{{\sum }_k(P(k|Y=0)P(Y=0)+P(k|Y=1)P(Y=1))}$$
  其中k表示X中的每一个词
  上述公式中：
• 分母：
  • P(“垃圾邮件”)等于样本中垃圾邮件的个数除以样本个数
  • P(k|“垃圾邮件”)等于垃圾邮件中单词k的个数，除以垃圾邮件词的总个数
• 分子：
  • $P(k|Y=0)$:正常邮件中出现单词k的个数，除以正常邮件词的总个数
  • P(Y=0)：正常邮件的个数除以样本总数
  • Y=1时同Y=0时。

由此可见，最终公式，分子、分母都可以计算了。
上述是用例子讲解的，朴素贝叶斯的纯数学表达式如下：

1.4