快速跳转
A-Monotonic Matrix
题意:输入n,m,求在一个n×m矩阵中填入{0,1,2},且保证每行每列都不下降的方案数。
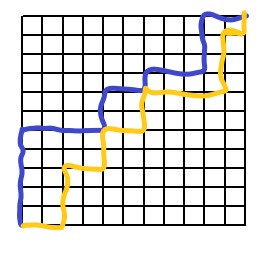
考虑这样一张网格图,向里面填入{0,1,2},由于每行每列都不下降,将图按填入的数字用分割线分开,那么{0,1},{1,2}之间的分割线必然都是从左下角到右上角的最短路径(即只会向左拐或者向上拐),否则无法保持单调性。
又根据上图易看出:{1,2}分割线必须不在{0,1}分割线上方(可以有重合,否则也会破坏单调性。
那么就可以由此建立模型:一张n×m的网格图,不妨令左下角坐标为(0,0),右上角为(n,m),(0,0)到(n,m)的最短路径集合为E,求集合T={(u,v)|u,v∈E,v在u方}的元素个数。
先考虑(0,0)到(n,m)的最短路径个数,每到一个点,都要选择向上或者向右走,共计要选择n+m次,而必须有m次是向左,n次是向右的,那么最短路径条数就是 C n + m m C_{n+m}^{m} Cn+mm
此时不考虑v是否在u的上方,总共两条最短路径有 C n + m m ⋅ C n + m m C_{n+m}^{m}·C_{n+m}^{m} Cn+mm⋅Cn+mm种情况
那么再减去v在u的上方的情况,就是答案了
而v不在u的上方有两种情况:u完全在v的上方(无公共点)和u,v有公共点(即给出的上图的情况)
可以做一些简单的处理,使其化为一种情况:将u的路径全部向上平移一格,v的路径全部向右平移一格,问题就转化为:求从(1,0)到(n+1,m)与(0,1)到(n,m+1)的不相交最短路径个数
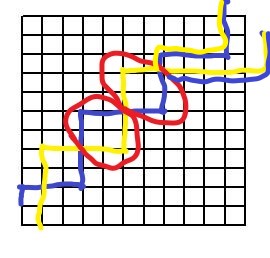
观察这张图,在红色区域内即相交部分,对所有相交的情况,都考虑最后一个交点,将最后一个交点的路径交换(即上图最后一部分)那么就变成了一个(0,1)到(n+1,m)的最短路和(1,0)到(n,m+1)的最短路。
再考虑(0,1)到(n+1,m)的最短路和(1,0)到(n,m+1)的最短路,这两条最短路是必相交的,那么对最后一个交点之后的路径交换,就成了一种(1,0)到(n+1,m)与(0,1)到(n,m+1)的相交路径。
很显然这是一个双射,因此(1,0)到(n+1,m)与(0,1)到(n,m+1)的相交路径个数即:(0,1)到(n+1,m)的最短路和(1,0)到(n,m+1)的最短路个数,即 C n + m m + 1 ⋅ C n + m n + 1 C_{n+m}^{m+1}·C_{n+m}^{n+1} Cn+mm+1⋅Cn+mn+1
那么答案就是 C n + m m ⋅ C n + m m − C n + m m + 1 ⋅ C n + m n + 1 C_{n+m}^{m}·C_{n+m}^{m}-C_{n+m}^{m+1}·C_{n+m}^{n+1} Cn+mm⋅Cn+mm−Cn+mm+1⋅Cn+mn+1
预处理一下,就变成了O(1)的询问,93ms即可过
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define Rii(x,y) scanf("%d%d",&x,&y)
const int N=2e3+5;
const ll MOD=1e9+7;
ll c[N][N];
int cal(int n,int m){
if(n<m) swap(n,m);
int a=min(m+1,n-1);
return (c[n+m][m]*c[n+m][m]+MOD*MOD-c[n+m][a]*c[n+m][m-1])%MOD;
}
int main(){
int n,m;
rep(i,0,2000) c[i][0]=1;
rep(i,1,2000)
rep(j,1,i)
c[i][j]=(c[i-1][j-1]+c[i-1][j])%MOD;
while(~Rii(n,m))
printf("%d\n",cal(n,m));
return 0;
}
B-Symmetric Matrix
题意:输入n,m,求满足 A i j ∈ { 0 , 1 , 2 } A_{ij}∈\{0,1,2\} Aij∈{ 0,1,2},主对角元全为0,行和为2的n阶对称矩阵A的个数
注意A的性质,对称矩阵,主对角元全为0,那么就可以看成是一张无向图的邻接矩阵,图中每个点的度均为2,很显然,这张图是仅由环构成的。
不妨设 a n a_{n} an是n个点时的情况个数,考虑插入第n+1个点时:
第一种情况是将n+1号点插入原来的两个点之间,由于n个点时图上有n条边,于是共有n个位置可以插入n+1,这时有 n a n na_{n} nan种情况,但是对于只有两个点的环,有两条边u,v,那么插入在u上和插入在v上的情况是一样的,于是要减去这些情况。而假设n+1号点插入在i,j形成的二元环内,此时其余的点共有 a n − 2 a_{n-2} an−2种情况,于是需要减去 C n 2 a n − 2 C_{n}^{2}a_{n-2} Cn2an−2,则此时情况个数是 n a n − n ( n − 1 ) 2 a n − 2 na_{n}-\frac{n(n-1)}{2}a_{n-2} nan−2n(n−1)an−2
第二种情况是原来n个点中选出一个与n+1构成一个二元环,共有 C n 1 a n − 1 C_{n}^{1}a_{n-1} Cn1an−1种情况。
于是可以得到递推式
a n + 1 = n ( a n + a n − 1 ) − n ( n − 1 ) 2 a n − 2 a_{n+1}=n(a_{n}+a_{n-1})-\frac{n(n-1)}{2}a_{n-2} an+1=n(an+an−1)−2n(n−1)an−2
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
#define rep(i,s,t) for(int i=s;i<=t;i++)
const int N=1e5+5;
int n;
ull m,f[N]={
0,0,1,1};
int main(){
while(~scanf("%d%lld",&n,&m)){
rep(i,4,n)
f[i]=((i-1)*(f[i-1]+f[i-2])+m-(f[i-3]*(i-1)*(i-2)/2)%m)%m;
printf("%lld\n",f[n]);
}
return 0;
}
C-Fluorescent 2
题意:有n个开关和m个灯泡,给定一个n×m的0,1矩阵,第(i,j)元为1代表开关按下灯泡会切换状态,初始时灯泡全部亮着。记一种按开关的方案为s,f(s)是这种方案中灯泡仍亮着的个数,方案的全集为S,求 ∑ s ∈ S ( f 3 ( s ) ) \sum_{s∈S}(f^3(s)) ∑s∈S(f3(s))
记 a s , i a_{s,i} as,i为第s个方案中第i个灯泡的状态,将式子展开得到(i,j,k可以相等)
∑ s ∈ S f 3 ( s ) = ∑ s ∈ S ( ∑ i , j , k a s , i a s , j a s , k ) \sum_{s∈S}f^3(s) = \sum_{s∈S}( \sum_{i,j,k}{a_{s,i}a_{s,j}a_{s,k}}) s∈S∑f3(s)=s∈S∑(i,j,k∑as,ias,jas,k)由求和的性质,交换一下求和符号,可以得到 ∑ s ∈ S ( ∑ i , j , k a s , i a s , j a s , k ) = ∑ i , j , k ( ∑ s ∈ S a s , i a s , j a s , k ) \sum_{s∈S}( \sum_{i,j,k}{a_{s,i}a_{s,j}a_{s,k}})=\sum_{i,j,k}( \sum_{s∈S}{a_{s,i}a_{s,j}a_{s,k}}) s∈S∑(i,j,k∑as,ias,jas,k)=i,j,k∑(s∈S∑as,ias,jas,k)
而 a i a j a k {a_ia_ja_k} aiajak当且仅当i,j,k均亮着时为1,那么 ∑ s ∈ S a s , i a s , j a s , k \sum\limits_{s∈S}{a_{s,i}a_{s,j}a_{s,k}} s∈S∑as,ias,jas,k即仅考虑i,j,k灯泡时,i,j,k三个灯泡均亮着的方案的个数,除以2^n,即三个灯泡均亮着的概率,那么就有 ∑ s ∈ S a s , i a s , j a s , k = 2 n P ( a s , i a s , j a s , k = 1 ) \sum\limits_{s∈S}{a_{s,i}a_{s,j}a_{s,k}}=2^nP(a_{s,i}a_{s,j}a_{s,k}=1) s∈S∑as,ias,jas,k=2nP(as,ias,jas,k=1)
于是可以得到 ∑ s ∈ S f 3 ( s ) = 2 n ⋅ ∑ i , j , k P ( a i a j a k = 1 ) \sum\limits_{s∈S}f^3(s) = 2^n·\sum\limits_{i,j,k}{P(a_ia_ja_k=1}) s∈S∑f3(s)=2n⋅i,j,k∑P(aiajak=1)
即求对任意i,j,k都亮着的概率和。又由灯泡亮着时该列1的个数为偶数,即异或和为0,那么只需求矩阵中任意选取三列,其中任取行向量异或和为零的概率和。
将矩阵的列向量的加法运算定义为异或运算,那么可以得到以{0,1}为域的线性空间(异或空间),考虑选出的三列构成n×3的矩阵,求出其行向量的极大线性无关组,将所有行向量张成一个异或线性空间,这个向量组即该空间的一组基,那么所有行向量都可由基经过异或运算以唯一的方式线性表出(基的性质)。
这时,考虑除了基之外的行向量,倘若异或和为0,就是一种合法的方案,倘若异或和不为0,那么就是一个该空间中的向量,可由基唯一表出,即可再异或一次该向量本身,成为0,那么又是一种合法方案。而只考虑基时,由于基线性无关,所以不可能有异或和为0的情况,因此设秩为r,所有合法的方案数即 2 n − r / 2 n = 1 / 2 r 2^{n-r}/2^n=1/2^r 2n−r/2n=1/2r
而该n×3的矩阵秩最大为3,所以可以求出所有秩为0,1,2,3的个数,再进行计算。又由矩阵的行秩等于列秩,那么只需计算选出的三列的列秩,而n的范围不超过50,则可以用long long 来记录列向量。
不明白可以搜索异或空间有关资料
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define Rii(x,y) scanf("%d%d",&x,&y)
const int N=1e3+5,MOD=1e9+7;
int s[4];
ll a[N],p[60]={
1};
pair<ll,int>b[N];
char d[N];
int main(){
int n,m,cnt;
rep(i,1,50) p[i]=(p[i-1]<<1)%MOD;
while(~Rii(n,m)){
rep(i,0,m) a[i]=0;
s[0]=s[1]=s[2]=s[3]=0;//秩为0,1,2,3的个数
rep(i,0,n-1){
scanf("%s",d);
rep(j,0,m-1)
a[j]=a[j]<<1|(d[j]=='1');
}
sort(a,a+m);
cnt=0;
rep(i,0,m-1)
if(!cnt||b[cnt-1].first<a[i]) b[cnt++]=make_pair(a[i],1);
else b[cnt-1].second++;
int z=b[0].first?0:b[0].second;//0的个数
s[0]=z*z*z;
rep(i,z>0,cnt-1)
s[1]+=(b[i].second+z)*(b[i].second+z)*(b[i].second+z)-s[0];
rep(i,z>0,cnt-1)
rep(j,i+1,cnt-1){
s[2]+=3*b[i].second*b[j].second*(2*z+b[i].second+b[j].second);
ll tmp=b[i].first^b[j].first;
int k=lower_bound(b,b+cnt,make_pair(tmp,0))-b;
if(k>j&&b[k].first==tmp)//存在b[k]=b[i]^[j],即线性相关
s[2]+=6*b[i].second*b[j].second*b[k].second;
}
s[3]=m*m*m-s[0]-s[1]-s[2];
int ans=(ll)s[0]*p[n]%MOD;
if(n>0) ans=(ans+(ll)s[1]*p[n-1])%MOD;
if(n>1) ans=(ans+(ll)s[2]*p[n-2])%MOD;
if(n>2) ans=(ans+(ll)s[3]*p[n-3])%MOD;
printf("%d\n",ans);
}
return 0;
}
D-Two Graphs
题意:如果存在一个双射Φ:V->W,V是图G的点集,W是图H的点集,满足边(u,v)存在当且仅当(Φ(u),Φ(v))存在,称G,H同构,求图G2或G2删去有限条边得到的图中与图G1同构的个数
由于最多只有8个点,用全排列暴力计算所有映射的情况,并记得除去G2自身同构的映射个数即可。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define ms0(ar) memset(ar,0,sizeof ar)
#define Rii(x,y) scanf("%d%d",&x,&y)
int a[10],n,m1,m2;
bool g1[10][10],g2[10][10];
bool ok(bool g[][10],bool h[][10]){
rep(i,1,n)
rep(j,1,n)
if(g[i][j]&&!h[a[i]][a[j]]) return 0;
return 1;
}
int main(){
while(~scanf("%d%d%d",&n,&m1,&m2)){
int u,v,cnt=0,ans=0;
ms0(g1);ms0(g2);
rep(i,1,n) a[i]=i;
rep(i,1,m1){
Rii(u,v);
g1[u][v]=g1[v][u]=1;
}
rep(i,1,m2){
Rii(u,v);
g2[u][v]=g2[v][u]=1;
}
do
if(ok(g1,g1)) cnt++;
while(next_permutation(a+1,a+n+1));
do
if(ok(g1,g2)) ans++;
while(next_permutation(a+1,a+n+1));
printf("%d\n",ans/cnt);
}
return 0;
}
E-Removal
题意:给定一个长度为n的序列s,求删除m个数后产生的不同子序列个数。
a[n]为给定的序列,dp[i][j][k]表示前i个数产生的序列中,长度为j,以数字k结尾的方案数,sum[i][j]表示前i个数产生的序列中长度为j的方案数。
考虑更新dp[i][j][k],只有在a[i]=k时更新,有dp[i][j][k]=sum[i-1][j-1],即长度为j-1的方案个数添上最后一位数字k
考虑更新sum[i][j],更新了dp[i][j][k]后,sum[i][j]加上dp[i][j][k],但这时候会有重复计算的方案,即假设数字k上一次出现的位置是p,那么由前p-1位构成的长度为j-1序列会计算两次添上数字a[i],因此要减去dp[p][j][k]
这时候可以写出更新的循环式子
for(int i=1;i<=n;i++){
for(int j=i;j>=max(i-m,0);j--)
dp[i][j][a[i]]=sum[i-1][j-1];
sum[i][j]+=dp[i][j][a[i]]-dp[p][j][a[i]];
}
}
对于其中的p,由于dp数组只有在a[i]=k时才更新第三维为k的,我们可以先调换一下循环的顺序
for(int i=1;i<=n;i++){
for(int j=i;j>=max(i-m,0);j--)
sum[i][j]+=sum[i-1][j-1]-dp[p][j][a[i]];
dp[i][j][a[i]]=sum[i-1][j-1];
}
}
可以发现,如果考虑将第一维滚动掉,使dp数组变成二维数组,那么未更新时的dp[j][a[j]]即dp[p][j][a[j]],于是可以写出
for(int i=1;i<=n;i++){
for(int j=i;j>=max(i-m,0);j--)
sum[j]+=sum[j-1]-dp[j][a[i]];
dp[j][a[i]]=sum[j-1];
}
}
再加上取模运算即可, 答案为sum[n-m]
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define per(i,s,t) for(int i=s;i>=t;i--)
#define ms0(ar) memset(ar,0,sizeof ar)
#define Ri(x) scanf("%d",&x)
#define Rii(x,y) scanf("%d%d",&x,&y)
const int N=1e5+5,MOD=1e9+7;
int dp[N][11],sum[N],s[N];
int main(){
int n,m,k;
while(~Rii(n,m)){
Ri(k);
ms0(dp);ms0(sum);
rep(i,1,n)
Ri(s[i]);
sum[0]=1;
rep(i,1,n){
int tmp=max(1,i-m-1);
per(j,i,tmp){
sum[j]+=(sum[j-1]-dp[j][s[i]]+MOD)%MOD;
sum[j]%=MOD;
dp[j][s[i]]=sum[j-1];
}
}
printf("%d\n",sum[n-m]);
}
return 0;
}
F-Sum of Maximum
题意:输入n个数,求 ∑ x 1 = 1 a 1 ∑ x 2 = 1 a 2 . . ∑ x n = 1 a n m a x { x 1 , . . . , x n } \sum\limits_{x_1=1}^{a_1}\sum\limits_{x_2=1}^{a_2}..\sum\limits_{x_n=1}^{a_n}max\{x_1,...,x_n\} x1=1∑a1x2=1∑a2..xn=1∑anmax{ x1,...,xn}
由于n个数是等价的,不妨先将其升序排序,然后将k的取值分成 [ 1 , a 1 ] , . . . , [ a i + 1 , a i + 1 ] , . . . [1,a_1],...,[a_i+1,a_{i+1}],... [1,a1],...,[ai+1,ai+1],...,假设最大值k取在第i个区间 [ a i − 1 + 1 , a i ] [ai−1+1,ai] [ai−1+1,ai],那么前i−1个数字无论取何值都不会超过最大值,故方案数为 ∏ j = 1 i − 1 a j \prod\limits_{j=1}^{i-1}a_j j=1∏i−1aj,而后n−i+1个数取值范围为[1,k],则方案数为 ∑ k = a i − 1 + 1 a i k [ k n − i + 1 − ( k − 1 ) n − i + 1 ] = ∑ k = a i − 1 + 1 a i [ k n − i + 2 − ( k − 1 ) n − i + 2 − ( k − 1 ) n − i + 1 ] = a i n − i + 2 − ( a i − 1 + 1 ) a i − 1 n − i + 1 − ∑ k = a i − 1 + 1 a i − 1 k n − i + 1 \begin{aligned} \sum\limits_{k=a_{i-1}+1}^{a_i}k[k^{n-i+1}-(k-1)^{n-i+1}]&= \sum\limits_{k=a_{i-1}+1}^{a_i}[k^{n-i+2}-(k-1)^{n-i+2}-(k-1)^{n-i+1}] \\ &=a_i^{n-i+2}-(a_{i-1}+1)a_{i-1}^{n-i+1}-\sum\limits_{k=a_{i-1}+1}^{a_i-1}k^{n-i+1} \end{aligned} k=ai−1+1∑aik[kn−i+1−(k−1)n−i+1]=k=ai−1+1∑ai[kn−i+2−(k−1)n−i+2−(k−1)n−i+1]=ain−i+2−(ai−1+1)ai−1n−i+1−k=ai−1+1∑ai−1kn−i+1
式子里比较难处理的是 ∑ k = a i − 1 + 1 a i − 1 k n − i + 1 \sum\limits_{k=a_{i-1}+1}^{a_i-1}k^{n-i+1} k=ai−1+1∑ai−1kn−i+1,易知这是k的n-i+2次多项式,于是可以求出n-i+3个值后用拉格朗日插值法求出多项式。
当然也可以根据 ∑ i = 1 n i k = 1 k + 1 ∑ i = 1 k + 1 C k + 1 i B k + 1 − i ( n + 1 ) i \sum\limits_{i=1}^ni^k=\frac{1}{k+1}\sum\limits_{i=1}^{k+1}C_{k+1}^iB_{k+1-i}(n+1)^i i=1∑nik=k+11i=1∑k+1Ck+1iBk+1−i(n+1)i(其中B是Bernoulli数, B 0 = 1 , B n = − 1 n + 1 ∑ j = 0 n − 1 C n + 1 j B j B_0=1,B_n=-\frac{1}{n+1}\sum\limits_{j=0}^{n-1}C_{n+1}^jB_j B0=1,Bn=−n+11j=0∑n−1Cn+1jBj),预处理出组合数和Bernoulli数后来求。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define per(i,s,t) for(int i=s;i>=t;i--)
#define ms0(ar) memset(ar,0,sizeof ar)
#define Ri(x) scanf("%d",&x)
const int N=1e3+5,MOD=1e9+7;
ll c[N][N],inv[N],b[N],a[N];
ll qpow(ll x,ll p){
ll ret=1;
while(p){
if(p&1) ret=(ret*x)%MOD;
x=(x*x)%MOD;
p>>=1;
}
return ret;
}
ll cal(ll n,int k){
n++,n%=MOD;
ll ret=0,tmp=n;
rep(i,1,k+1){
ret=(ret+c[k+1][i]*b[k+1-i]%MOD*n%MOD)%MOD;
n=n*tmp%MOD;
}
ret=ret*inv[k+1]%MOD;
return ret;
}
void init(){
c[0][0]=1;
rep(i,1,N-1){
rep(j,1,i)
c[i][j]=(c[i-1][j-1]+c[i-1][j])%MOD;
c[i][0]=1;
}
inv[1]=1;
rep(i,2,N-1)
inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
b[0]=1;
rep(i,1,N-1){
b[i]=0;
rep(k,0,i-1)
b[i]=(b[i]+c[i+1][k]*b[k]%MOD)%MOD;
b[i]=(b[i]*(MOD-inv[i+1])%MOD+MOD)%MOD;
}
}
int main(){
init();
int n;
while(~Ri(n)){
rep(i,1,n)
scanf("%lld",&a[i]);
sort(a+1,a+n+1);
ll mul=1,ans=0;
rep(i,1,n){
if(a[i]!=a[i-1]){
ll s1=(qpow(a[i],n-i+2)+MOD-qpow(a[i-1],n-i+1)*(a[i-1]+1)%MOD)%MOD;
ll s2=(cal(a[i]-1,n-i+1)+MOD-cal(a[i-1],n-i+1))%MOD;
s1=(s1-s2+MOD)%MOD;
ans=(ans+s1*mul)%MOD;
}
mul=mul*a[i]%MOD;
}
printf("%lld\n",ans);
}
return 0;
}
G-Steiner Tree
题意:求Steiner Tree的个数
Steiner Tree: Steiner Tree问题是组合优化学科中的一个问题。将指定点集合中的所有点连通,且边权总和最小的生成树称为最小Steiner Tree。
求Steiner Tree是通过dp进行的,dp[i][j]表示i状态下以j为根的子树的权值,其中状态i用状态压缩以一个二进制数表示在树上的点集。
状态转移分为两部分:
第一部分是枚举以j为根的两个子树,状态转移方程为 d p [ i ] [ j ] = m i n ( d p [ i ] [ j ] , d p [ a ] [ j ] + d p [ b ] [ j ] ) dp[ i ][ j ]=min(dp[ i ][ j ],dp[ a ][ j ]+dp[ b ][ j ]) dp[i][j]=min(dp[i][j],dp[a][j]+dp[b][j]),其中a,b是i的一个划分,即a&b=i且a|b=0
第二部分是以边进行松弛,类似于最短路的松弛,即 d p [ i ] [ j ] = m i n ( d p [ i ] [ j ] , d p [ i ] [ k ] + w [ j ] [ k ] ) dp[ i ][ j ]=min(dp[ i ][ j ],dp[ i ][ k ]+w[ j ][ k ] ) dp[i][j]=min(dp[i][j],dp[i][k]+w[j][k]),而本题中所有边权都是1,这个状态转移很显然可以用最短路的算法做
然后考虑求方案数,首先第一种状态转移是由最短路得到的,不会有重复的情况,考虑第二种状态转移,类似于前面图的同构题,以这棵生成树不同的节点为根出发得到的树都是同构的,因此一个状态的划分可能会被统计多次,会重复计算,所以应该指定一个节点,其中一个划分必须包含这个节点来进行计算,而最简单的处理办法就是以该状态下最小的节点为指定节点。
因此可以用f,g两个数组来储存,其中f储存经过第一部分dp之后得到的树,然后f的状态必须包含指定节点,以此来进行第二部分dp更新g,之后在第一部分dp中再以g更新一下f。
可能会T,要多交几次。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,int> pii;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define ms0(ar) memset(ar,0,sizeof ar)
#define ms1(ar) memset(ar,-1,sizeof ar)
#define Rii(x,y) scanf("%d%d",&x,&y)
#define d first
#define way second
#define mp make_pair
const int K=15,N=60,M=2e3+5,MOD=1e9+7,INF=0x3f3f3f3f;
pii operator+(const pii &x,const pii &y){
//重载+
return mp(x.d+y.d,x.way*y.way%MOD);
}
inline void upd(pii &x,const pii &y){
//更新方案
if(x.d>y.d) x=y;
else if(x.d==y.d) x.way=(x.way+y.way)%MOD;
}
int lowbit(int x){
return x&(-x);
}
bool vis[N];
int n,m,k,cnt,fst[N],nxt[M],to[M];
priority_queue<pii,vector<pii>,greater<pii> >q;
void dijkstra(pii *g,pii *f){
ms0(vis);
rep(i,1,n)
if(g[i].d!=INF) q.push(mp(g[i].d,i));
while(!q.empty()) {
pii x=q.top();q.pop();
int u=x.second;
if(vis[u]) continue;
vis[u]=1;
for(int i=fst[u];~i;i=nxt[i]){
int v=to[i];
if(g[v].d>g[u].d){
upd(g[v],g[u]+mp(1, 1));
upd(f[v],g[u]+mp(1, 1));
q.push(mp(g[v].d,v));
}
}
}
}
pii f[1<<K][N],g[1<<K][N];
void cal(){
rep(s,0,(1<<k)-1)
rep(i,1,n)
g[s][i]=f[s][i]=mp(INF,0);
rep(i,1,k)
g[1<<(i-1)][i]=f[1<<(i-1)][i]=mp(0,1);
rep(s,0,(1<<k)-1){
for(int t=(s-1)&s;t;t=(t-1)&s)
if(lowbit(s)==lowbit(t))//以s的最小编号的点为指定点
rep(i,1,n)
upd(g[s][i],f[t][i]+g[s^t][i]);
dijkstra(g[s],f[s]);
}
printf("%d\n",g[(1<<k)-1][1].way);
}
void add(int x,int y){
nxt[cnt]=fst[x];
fst[x]=cnt;
to[cnt++]=y;
}
int main(){
while(~scanf("%d%d%d",&n,&m,&k)){
ms1(fst);
cnt=0;
int u,v;
rep(i,1,m){
Rii(u,v);
add(u,v);
add(v,u);
}
cal();
}
return 0;
}
H-Longest Path
树上DP+斜率优化,暂时不会
I-Substring
题意:如果存在一个同构映射使字符串s映射到t,则称s,t同构,给定一个由{a,b,c}构成的字符串,求不同构的子串个数。
要涉及所有子串,很显然用字符串做,而字符串只由{a,b,c}构成,那么只有六种映射,直接把六个字符串连接起来用后缀数组做即可,不过需要特殊考虑全部为同一个字母的子串只有三种映射形式
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define per(i,s,t) for(int i=s;i>=t;i--)
#define Ri(x) scanf("%d",&x)
const int N=3e5+100,M=10;
int s[N],sa[N],rk[N],cnt[N],tp[N],h[N],n,m,w,mp[6][3]={
{
1,2,3},{
1,3,2},{
2,1,3},{
2,3,1},{
3,1,2},{
3,2,1}};
void bsort(){
rep(i,0,m) cnt[i]=0;
rep(i,1,n) cnt[rk[i]]++;
rep(i,1,m) cnt[i]+=cnt[i-1];
per(i,n,1) sa[cnt[rk[tp[i]]]--]=tp[i];
}
void gsark(){
m=M;
rep(i,1,n)
rk[i]=s[i],tp[i]=i;
bsort();
int p;
for(w=1,p=0;p<n;m=p,w<<=1){
p=0;
rep(i,1,w) tp[++p]=n-w+i;
rep(i,1,n)
if(sa[i]>w)
tp[++p]=sa[i]-w;
bsort();
swap(tp,rk);
rk[sa[1]]=p=1;
rep(i,2,n)
rk[sa[i]]=(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+w]==tp[sa[i]+w])?p:++p;
}
}
void gh(){
int k=0;
rep(i,1,n){
if(k) k--;
int j=sa[rk[i]-1];
while(s[i+k]==s[j+k]) k++;
h[rk[i]]=k;
}
}
char ch[N+5];
int main(){
int nn;
while(~Ri(nn)){
scanf("%s",ch+1);
n=-1;
int l=1,ml=1;
rep(i,2,nn)
if(ch[i]==ch[i-1]) l++,ml=max(ml,l);
else l=1;
rep(i,0,5){
s[++n]=4+i;
rep(j,1,nn)
s[++n]=mp[i][ch[j]-'a'];
}
gsark();
gh();
ll ans=3ll*nn*(nn+1);
rep(i,1,n)
ans-=h[i];
printf("%lld\n",(ans+3*ml)/6);
}
return 0;
}
J-Different Integers
应该是相对来说好做的题?附上zzx大佬的莫队做法
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 200010;
int n,m,num,a[N];
struct data{
int l,r,id,block;
bool operator < (const data &a) {
if(block == a.block) return r < a.r;
return block < a.block;
}
}q[N];
int cnt[N],ans[N];
/*
bool cmp(data a,data b)
{
if(a.block==b.block) return a.r<b.r;
return a.block < b.block;
}*/
int tmp;
void add(int x) {
cnt[a[x]]++;
if(cnt[a[x]]==1)tmp++;
}
void del(int x) {
cnt[a[x]]--;
if(!cnt[a[x]])tmp--;
}
void Solve() {
int l=1,r=0;
for(int i=1;i<=m;i++) {
while(l<q[i].l) del(l),l++;
while(l>q[i].l) l--,add(l);
while(r<q[i].r) r++,add(r);
while(r>q[i].r) del(r),r--;
ans[q[i].id]=tmp;
}
}
int main() {
while(~scanf("%d%d",&n,&m)) {
num=sqrt(n * 2);
memset(cnt,0,sizeof cnt);
memset(ans,0,sizeof ans);
tmp = 0;
for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
for(int i = n + 1;i <= 2 * n;++ i) a[i] = a[i - n];
//for(int i=1;i<=m;++i)
for(int l,r,i=1;i<=m;i++) {
scanf("%d%d",&l,&r);
q[i].l = r,q[i].r = n + l;
q[i].id=i;
q[i].block=(q[i].l-1)/num+1;
}
sort(q+1,q+m+1);
Solve();
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
}
return 0;
}