回归算法
回归,指研究一组随机变量(Y1 ,Y2 ,…,Yi)和另一组(X1,X2,…,Xk)变量之间关系的统计分析方法,又称多重回归分析。通常Y1,Y2,…,Yi是因变量,X1、X2,…,Xk是自变量。
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。例如,司机的鲁莽驾驶与道路交通事故数量之间的关系,最好的研究方法就是回归。
常见的回归算法
Linear Regression线性回归
它是最为人熟知的建模技术之一。线性回归通常是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
线性回归使用最佳的拟合直线(也就是回归线)在因变量(Y)和一个或多个自变量(X)之间建立一种关系。
用一个方程式来表示它,即Y = a x + b + ϵ Y=ax + b + \epsilonY=ax+b+ϵ,其中a表示直线的斜率,b表示截距,e是误差项。这个方程可以根据给定的预测变量(s)来预测目标变量的值。
Logistic Regression逻辑回归
逻辑回归是用来计算“事件=Success”和“事件=Failure”的概率。当因变量的类型属于二元(1 / 0,真/假,是/否)变量时,我们就应该使用逻辑回归。他广泛的用于分类问题。
Polynomial Regression多项式回归
对于一个回归方程,如果自变量的指数大于1,那么它就是多项式回归方程。如下方程所示:
y = a ∗ x 2 + b y=a*x^2+by=a∗x2+b
在这种回归技术中,最佳拟合线不是直线。而是一个用于拟合数据点的曲线。过拟合欠拟合问题.在多项式回归中非常常见.
Stepwise Regression逐步回归
在处理多个自变量时,我们可以使用这种形式的回归。在这种技术中,自变量的选择是在一个自动的过程中完成的,其中包括非人为操作。
这一壮举是通过观察统计的值,如R-square,t-stats和AIC指标,来识别重要的变量。逐步回归通过同时添加/删除基于指定标准的协变量来拟合模型。下面列出了一些最常用的逐步回归方法:
标准逐步回归法做两件事情。即增加和删除每个步骤所需的预测。
向前选择法从模型中最显著的预测开始,然后为每一步添加变量。
向后剔除法与模型的所有预测同时开始,然后在每一步消除最小显着性的变量。
这种建模技术的目的是使用最少的预测变量数来最大化预测能力。这也是处理高维数据集的方法之一。
Ridge Regression岭回归
岭回归分析是一种用于存在多重共线性(自变量高度相关)数据的技术。在多重共线性情况下,尽管最小二乘法(OLS)对每个变量很公平,但它们的差异很大,使得观测值偏移并远离真实值。岭回归通过给回归估计上增加一个偏差度,来降低标准误差。
Lasso Regression套索回归
它类似于岭回归,Lasso (Least Absolute Shrinkage and Selection Operator)也会惩罚回归系数的绝对值大小。此外,它能够减少变化程度并提高线性回归模型的精度。
ElasticNet回归
ElasticNet是Lasso和Ridge回归技术的混合体。它使用L1来训练并且L2优先作为正则化矩阵。当有多个相关的特征时,ElasticNet是很有用的。Lasso 会随机挑选他们其中的一个,而ElasticNet则会选择两个。
——以上部分内容摘自腾讯云社区的陆勤_数据人网发布的算法:其中常用的回归算法.
线性回归
概念
线性回归(Linear Regression) 顾名思义,是基于线性模型的回归分析.是最为人熟知的建模技术之一。线性回归通常是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
线性回归使用最佳的拟合直线(也就是回归线)在因变量(y)和一个或多个自变量(x)之间建立一种关系。
用一个方程式来表示它,即y=ax + b + ε,其中a表示直线的斜率,b表示截距, ε是误差项。这个方程可以根据给定的预测变量(s)来预测目标变量的值。
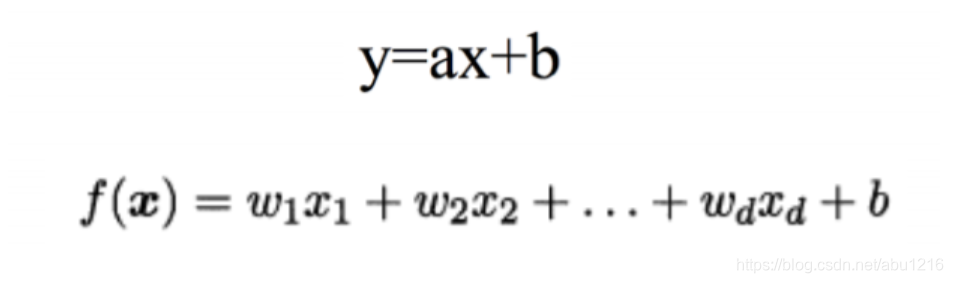
上图包含两个公式,上边的公式大家非常熟悉就是我们学生时代学习的二维空间中的一次函数,函数图像是一条直线.而下边的公式也很好理解,他只是在维度发生了改变,是多维空间中的一条直线.函数图像是直线,我们称之为线性,是否线性只需要观察函数中是否只有一次项即可.只要都是一次项那么不管几维空间,他都是直线.另外,从项数来区分,分为一元线性回归和多元线性回归.
线性方程知识回顾
假设我们有如下的一个二元一次方程:
y = ax + b
并且我们已知两个点在这个函数图像上
A:(1,3) 和 B:(2,5)
将两个点带入方程
a + b = 3
2a + b = 5
解得: a = 2, b = 1
那么方程为:y = 2x + 1
此时:在函数图像上给出任意一个点的x坐标,我们都可以根据这个方程来求出其对应的y坐标.
从这个简单的案例中,我们体会到的其实就是根据现有数据(AB两个点),选择合适的数学模型(f(x) = ax + b),并根据数据和模型的关系求解出模型具体的函数,再通过求解出的函数预测其他自变量所对应的应变量的近似值的过程.
线性模型
不幸的是,这样完美的模型一般情况下只存在数学世界,而生活中的事物在满足某些规律的基础上往往还收到其他因素的干扰,这种被干扰的情况我们称之为包含噪声(with noise)
包含噪声的函数这样来表示:f ( x ) = a x + b + ε f(x) = ax + b + εf(x)=ax+b+ε
ε(Epsilon) ~ N(0,1) : 噪声值,满足高斯分布(正态分布)
注:什么是高斯分布(正态分布)? 指在一组相关样本数据中,所有样本数据的分布状态为越靠近平均数样本数据越密集,越远越稀疏,如图:

而噪声ε~N(0,1)指正常状态下(大部分数据)噪声为0
现在我们有如下一组数据:
ID,Education,Income
1,10.000000 ,26.658839
2,10.401338 ,27.306435
3,10.842809 ,22.132410
4,11.244147 ,21.169841
5,11.645449 ,15.192634
6,12.086957 ,26.398951
7,12.048829 ,17.435307
8,12.889632 ,25.507885
9,13.290970 ,36.884595
10,13.732441 ,39.666109
11,14.133779 ,34.396281
12,14.635117 ,41.497994
13,14.978589 ,44.981575
14,15.377926 ,47.039595
15,15.779264 ,48.252578
16,16.220736 ,57.034251
17,16.622074 ,51.490919
18,17.023411 ,51.336621
19,17.464883 ,57.681998
20,17.866221 ,68.553714
21,18.267559 ,64.310925
22,18.709030 ,68.959009
23,19.110368 ,74.614639
24,19.511706 ,71.867195
25,19.913043 ,76.098135
26,20.354515 ,75.775216
27,20.755853 ,72.486055
28,21.167191 ,77.355021
29,21.598662 ,72.118790
30,22.000000 ,80.260571
根据数据进行图像绘制
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
# 通过pd读取文件
data = pd.read_csv('./data.csv')
x = data.Education
y = data.Income
# 通过plt绘制图像
plt.scatter(x, y)
plt.show()
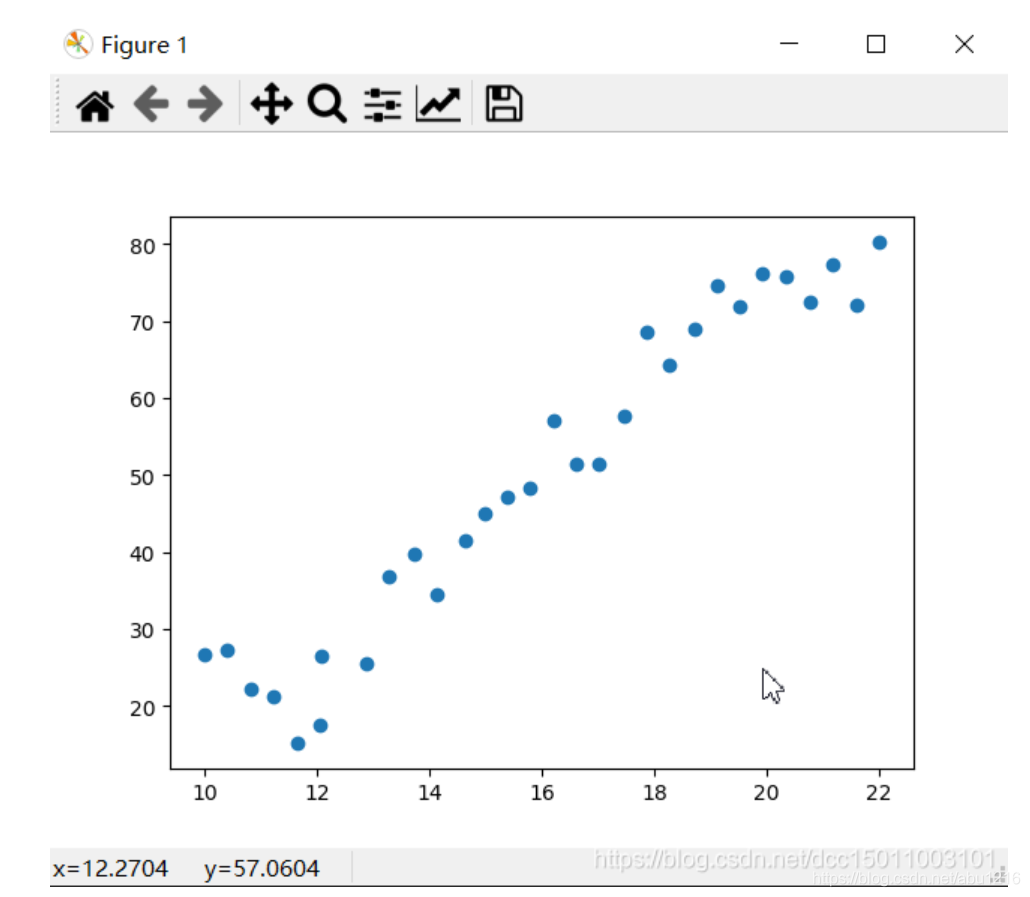
通过观察,我们发现这组数据基本符合线性函数的图像特征,只是在数据个体中可能存在噪声.
那么我们可以尝试选择f(x) = ax + b + ε这个函数来进行建模.
但是,此时的函数图像和数据虽然与刚才的简单案例相近,但是由于噪声的存在,所以不能只是简单的代入数据后求解.那么这种情况如何解决呢?
最小二乘法
基于均方误差最小化来进行模型求解的方法称为"最小二乘法"(ordinary least squares) 他的主要思想就是选择未知参数,使得理论值与测试值之差的平方和达到最小.
我们先来整理以下思路:
- 我们知道,在这组数据中,我们不可能画出一条直线穿过所有点,因为包含噪声,而通过观察函数式, 我们发现噪声在图像上的体现就是让原本在直线上的点出现了上或下的平移, 平移距离即为ε的绝对值.
- 而ε ~ N(0,1),所以我们先可以假设有一条直线是我们最终要求得的模型,然后将所有的数据代入这条我们预估的直线中,并求出所有点ε值, 当ε总和最小时,函数图像与样本数据的误差即最小,此时我们能够确定两个未知数a和b的值.
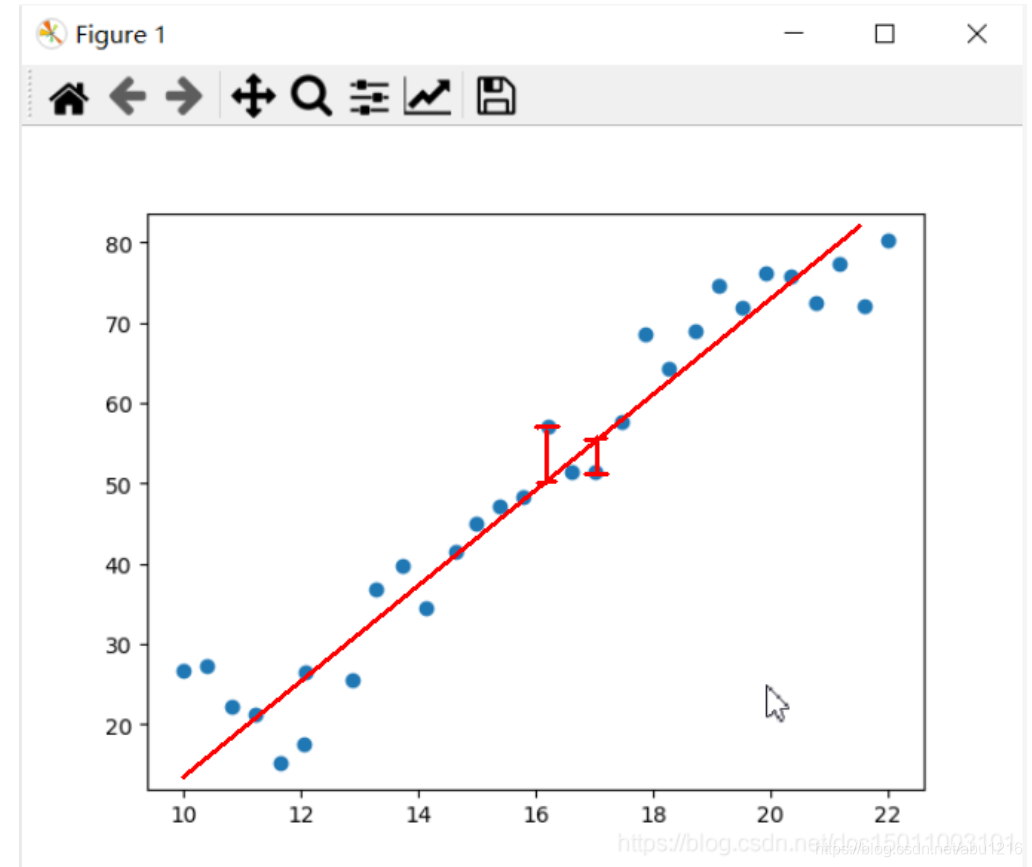
那么什么时候能够满足ε总和最小呢?
整理一下公式:
f ( x ) = a x + b + ε f(x) = ax + b + εf(x)=ax+b+ε
先来尝试计算一下ε的值:
ε = y i − f ( x i ) ⇒ ε = y i − a x i − b ε = y_i - f(x_i) ⇒ ε = y_i - ax_i - bε=yi−f(xi)⇒ε=yi−axi−b
此时对应不同的值(xi,yi), 有ε为正或负.因为需要将所有点的ε进行求和所以为了屏蔽ε有为负可能的影响,我们可以对他求平方.即.
ε 2 ε^2ε2 = ( y i − a x i − b ) 2 (y_i - ax_i - b)^2(yi−axi−b)2
对所有点上的ε 2 ε^2ε2进行求和得到:
E = Σ i = 1 m \Sigma^m_{i=1}Σi=1m ( y i − a x i − b ) 2 (y_i - ax_i - b)^2(yi−axi−b)2 也就是损失函数(loss function),也记做:loss = Σ i = 1 m \Sigma^m_{i=1}Σi=1m ( y i − a x i − b ) 2 (y_i - ax_i - b)^2(yi−axi−b)2
其中 i∈[1,m] 代表所有点,当E最小时 a 和 b的值有唯一解.见下图,(w即a)
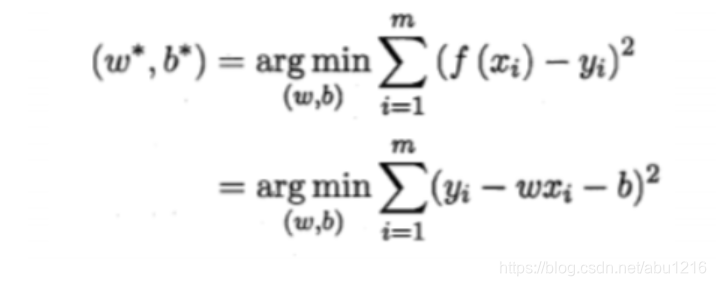
那么如何找到 loss 的最小值呢?这里我们需要对二次函数有一个基本认识,二次函数的图像如下:
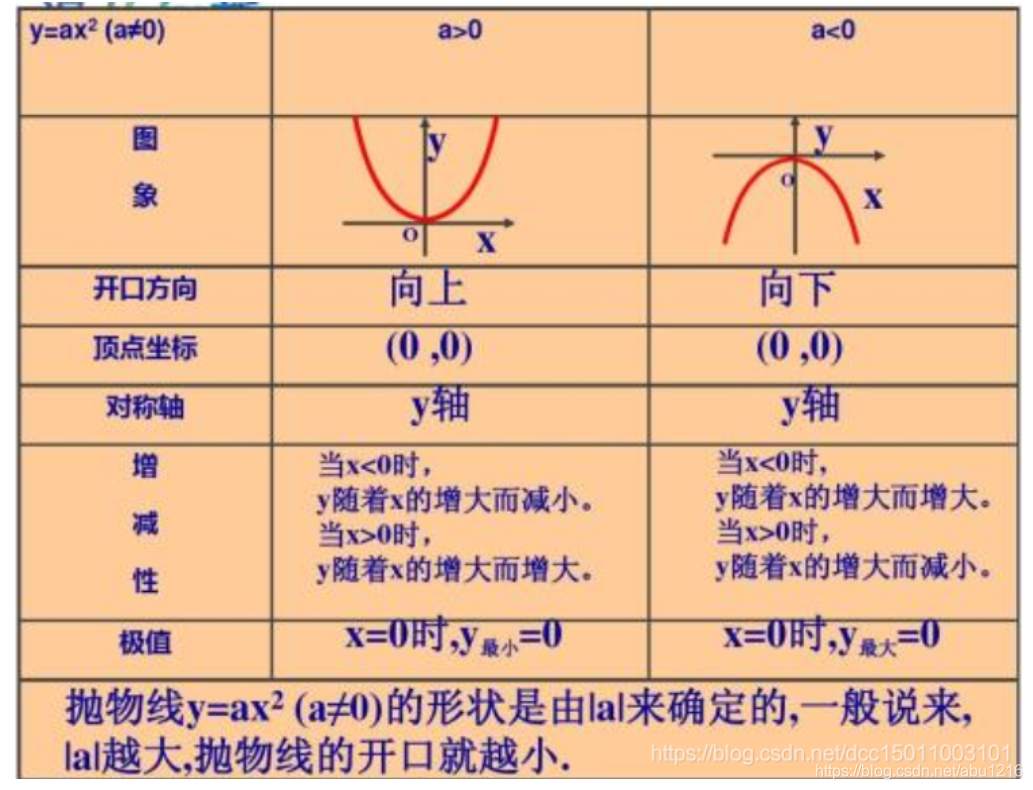
回顾二次函数知识得知,当二次项系数为正时,函数开口向上,有最小值.而进一步计算刚刚我们得到的公式: l o s s = Σ i = 1 m loss = \Sigma^m_{i=1}loss=Σi=1m ( y i − a x i − b ) 2 (y_i - ax_i - b)^2(yi−axi−b)2
其中x i , y i x_i,y_ixi,yi均为已知常数,未知数为a 和 b .− x i -x_i−xi和− 1 -1−1的平方都为正,所以图像为开口向上,即有最小值.
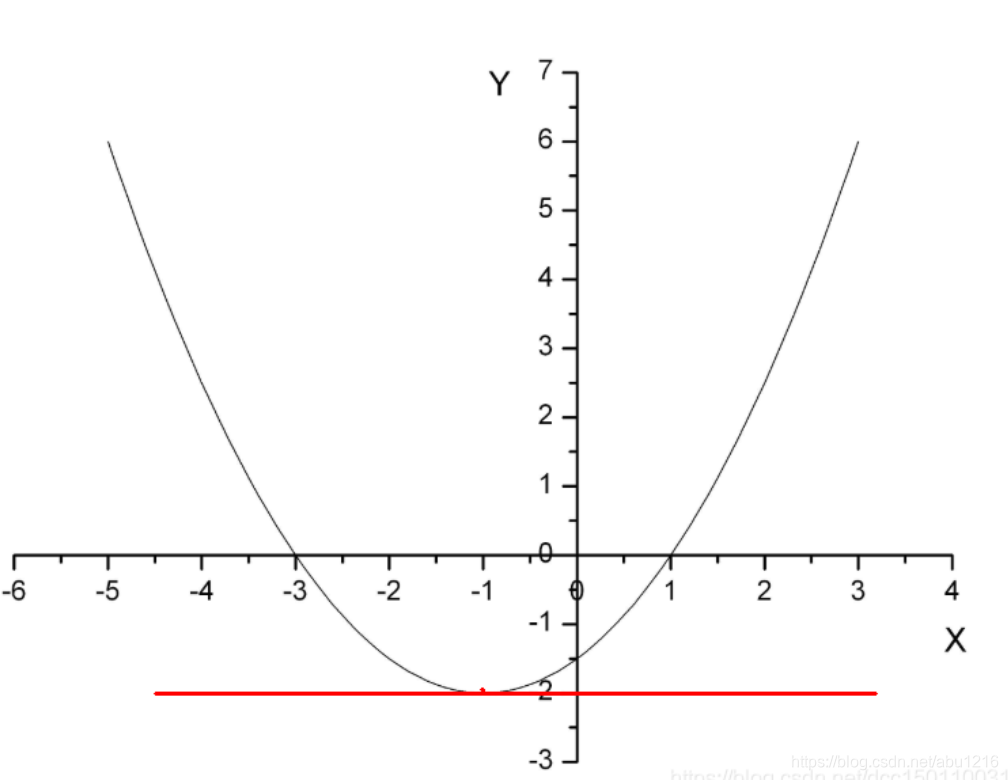
求该函数最小值是比较简单的,只要对函数进行求导,当导数(切线斜率)为0时,如图红线,即得 loss 的最小值.
有两个未知数,我们先求w(即a,x的系数)的偏导,得出w后代入求b的导数.
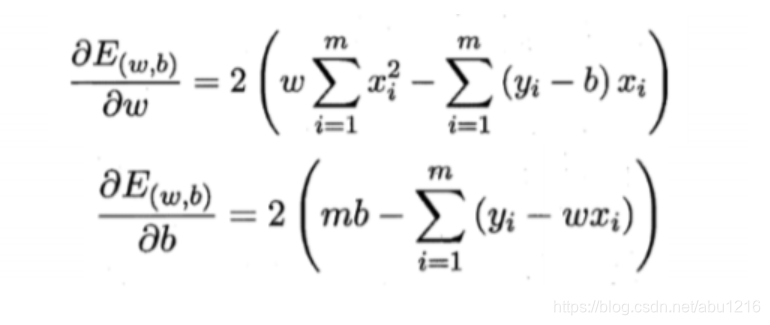
令w和b的偏导数都为0可以解得:
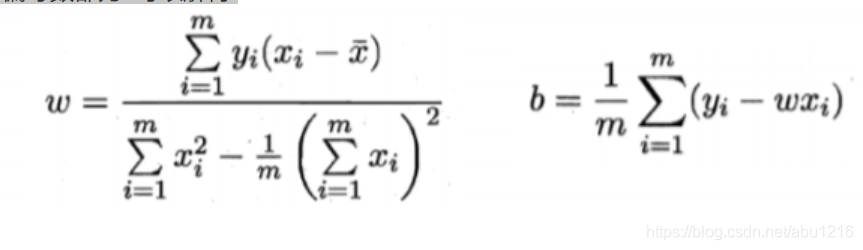
其中:
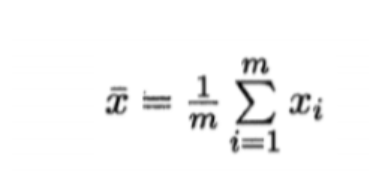
此时我们就可以得到对于这组样本数据的完美拟合模型.
代码实现
# 线性回归求解之最小二乘法
# 1.引入依赖
import pandas as pd
import matplotlib.pyplot as plt
# 2.读取数据
points = pd.read_csv('data.csv')
x = points.Education
y = points.Income
# *3.展示图像
# plt.scatter(x, y)
# plt.show()
# 3.定义函数计算平均数
def average(data):
sum = 0
num = len(data)
for i in range(num):
sum += data[i]
return sum / num
# 4.定义拟合函数,并求出w和b
def fit_function(x, y):
"""
拟合函数
:param x: x坐标集合
:param y: y坐标集合
:return: w,b :斜率,截距
"""
m = len(x)
# 求得所有x的平均数
x_bar = average(x)
# 根据公式准备数据
sum_yxxbar = 0
sum_x2 = 0
sum_ywx = 0
for i in range(m):
sum_yxxbar += y[i] * (x[i] - x_bar)
sum_x2 += x[i] ** 2
w = sum_yxxbar / (sum_x2 - m * (x_bar ** 2))
for i in range(m):
sum_ywx += (y[i] - w * x[i])
b = sum_ywx / m
return w, b
w, b = fit_function(x, y)
# 5.定义误差函数,求出误差值
def MSE(w, b, x, y):
"""
均方误差
:param w:斜率
:param b:截距
:param x:x坐标集合
:param y:y坐标集合
:return:均方误差
"""
total_loss = 0
m = len(x)
for i in range(m):
total_loss += (y[i] - w * x[i] - b) ** 2
return total_loss / m
print("w is :", w)
print("b is :", b)
loss = MSE(w, b, x, y)
print("loss is :", loss)
# 6.在样本数据图像上画出拟合函数图像
plt.scatter(x, y)
y = w * x + b
plt.plot(x, y, c='r')
plt.show()
执行结果:

最小二乘法在一元线性回归中的计算是非常精准的,但是如果模型为多元线性模型,图像是多维空间中的直线,这种情况如图:
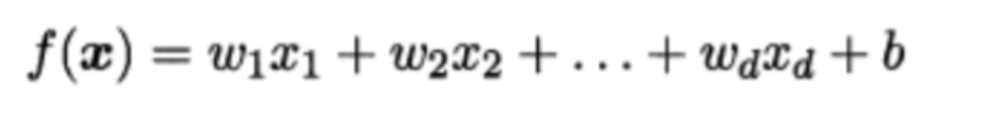
那么计算量(导函数求解)也是非常大的.为了避免复杂的计算过程,我们可以放弃精准结果退而求其次,采用近似逼近的方式来解决这个问题.如何实现呢?下面介绍另外一种求解线性回归更加常用的方法:梯度下降算法.
梯度下降算法
梯度下降(Gradient Descent)是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。
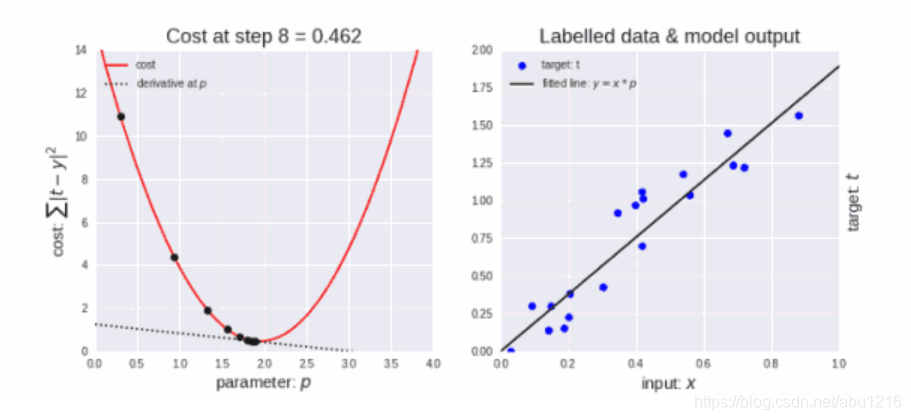
代码实现
# 线性回归求解之梯度下降法
# 1.引入依赖
import pandas as pd
import matplotlib.pyplot as plt
# 2.读取数据
points = pd.read_csv('data.csv')
x = points.Education
y = points.Income
# *3.展示图像
# plt.scatter(x, y)
# plt.show()
# 3.定义损失函数(MSE)
def MSE(w, b, x, y):
"""
均方误差
:param w:斜率
:param b:截距
:param x:x坐标集合
:param y:y坐标集合
:return:均方误差
"""
total_loss = 0
m = len(x)
for i in range(m):
total_loss += (y[i] - w * x[i] - b) ** 2
return total_loss / m
# 4.初始化模型的超参数
alpha = 0.0001 # 步长系数用于控制下降速度
initial_w = range(2, 8) # 初始化w
initial_b = range(-50, -30) # 初始化b
num_iter = 200 # 迭代次数
# 5.定义梯度下降算法
def gradient_descent(x, y, initial_w, initial_b, alpha, num_iter):
"""
定义梯度下降算法
:param x: 样本点x坐标
:param y: 样本点y坐标
:param initial_w: 初始w
:param initial_b: 初始b
:param alpha: 步长系数
:param num_iter: 迭代次数
:return: 最终w,b,损失值集合(记录损失下降过程)
"""
w = initial_w
b = initial_b
loss_list = []
for i in range(num_iter):
loss = MSE(w, b, x, y)
if i % 10 == 0: # 每十次输出一次当前结果
print("step:", i, "|w| is :", w, "|b| is :", b, "|loss| is :", loss)
loss_list.append(loss)
w, b = step_gradient_descent(w, b, alpha, x, y)
return [w, b, loss_list] # 返回结果list
# 6.梯度下降过程
def step_gradient_descent(w, b, alpha, x, y):
"""
单次梯度下降
:param w: 当前斜率
:param b: 当前截距
:param alpha: 步长系数用于控制下降速度
:param x: 样本点x坐标
:param y: 样本点y坐标
:return: step_w, step_b本次下降后的斜率和截距
"""
sum_grad_w = w
sum_grad_b = b
m = len(x)
# 计算w和b的偏导
for i in range(m):
sum_grad_w += (w * x[i] + b - y[i]) * x[i]
sum_grad_b += w * x[i] + b - y[i]
grad_w = 2 / m * sum_grad_w
grad_b = 2 / m * sum_grad_b
# 梯度下降
step_w = w - alpha * grad_w
step_b = b - alpha * grad_b
return step_w, step_b
# 7.多点求解
# 定义最终结果
final_loss_list = [1000]
final_w = 0
final_b = 0
# 遍历多点进行计算并保留最优解
def comput_multipoint(x, y, initial_w, initial_b, alpha, num_iter):
"""
遍历多点进行计算并保留最优解
:param x: 样本点x坐标
:param y: 样本点y坐标
:param initial_w: 初始斜率范围
:param initial_b: 初始截距范围
:param alpha: 步长系数用于控制下降速度
:param num_iter: 迭代次数
:return: None
"""
# 引入全局变量
global final_loss_list
global final_w
global final_b
# 遍历所有w,b进行组合尝试
for w in initial_w:
for b in initial_b:
result_list = gradient_descent(x, y, w, b, alpha, num_iter)
if min(result_list[2]) < min(final_loss_list):
final_w = result_list[0]
final_b = result_list[1]
final_loss_list = result_list[2]
print("=" * 10 + "最新loss:", min(result_list[2]), "=" * 10)
# w, b, loss_list = gradient_descent(x, y, initial_w, initial_b, alpha, num_iter)
# 8.调用函数并输出结果
comput_multipoint(x, y, initial_w, initial_b, alpha, num_iter)
# 日志输出
print("w is :", final_w)
print("b is :", final_b)
print("loss is :", min(final_loss_list))
# 损失变化图像绘制
plt.plot(final_loss_list)
plt.show()
# 在样本数据图像上画出拟合函数图像
plt.scatter(x, y)
y = final_w * x + final_b
plt.plot(x, y, c='r')
plt.show()