名词解释请看这篇博客:频谱分析和FFT算法总结
一.离散傅里叶变换(DFT)的理论
已知傅里叶变换和傅里叶逆变换,变换如下:
正变换:
![]()
逆变换:
![]()
离散傅里叶变换(DFT)顾名思义就是对傅里叶变换进行离散化,包括频率和时间的离散化,我们令 和
,代入傅里叶正变换中,得:
![]()
将积分变为求和得:

取N点进行时域截断得:

考虑到 就是离散化后第n点的时间函数值
,
就是离散化后第k点的傅里叶变换值
,
进行归一化处理,所以DFT的定义如下:

其中用到了欧拉公式。
DFT的实部和虚部分别为:
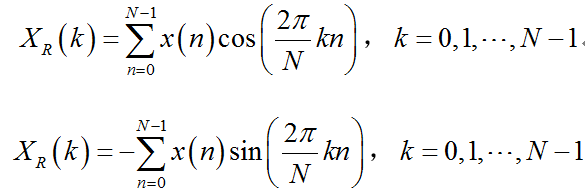
令, 则有
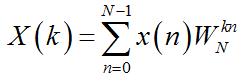
其中 算子的周期为N,模为1的复数。上式写成矩阵形式会更容易理解,如下:

上式中是已知的,可以很容易根据
计算出
,当N取值很大的很大的时候,上述方程组的求解计算量很大,
级的计算复杂度,由于
的周期性,主动选择合适的N可以更快的求解方程组,于是出现了基2型FFT算法。
二.快速傅里叶变换(FFT)的实现流图
FFT算法的基本思路,本质上就是怎么更快的计算上面的方程组。
先来看一下FFT算法的速度有多快,如表1所示

FFT算法有种二分的思想,首先将数据分为奇数序列和偶数序列两部分,然后再对每个序列进行二分,直到最后分成2个点的计算,也就是求解一元二次方程组。步骤如下:

其中,

式中,为
的N点DFT,用两个N/2点DFT的
和
表示,两者分别是
偶数样本和奇数样本的DFT。

根据, 有
, 所以
![]()
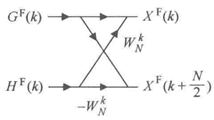
对于每一个k,图1所示只需要一次乘法和加减各一次,重复上述过程直至产生2点DFT。
下面以N=8为例介绍FFT算法(直接截图表示哈)


N=8时FFT计算流图如图2所示:

参考文献
1. 丁康,谢明等. 离散傅里叶分析校正理论与技术[M]
2. 卡米赛提.拉姆莫汉.饶, 金道年. 快速傅里叶变换:算法与应用[M]