【Programming Languages And Lambda calculi】4.6 Lambda表达式 递归 （重要，建议彻底弄懂）

4.6 递归

上一小节的练习要求你用实现 add 的方法实现 mult 。类似的实现体现了数字是由函数编码的信息。

给定函数 iszero，add和 sub1，我们同样可以在不知道任何数值如何被编码的前提下实现 mult 。我们必须定义一个递归程序来检查第一个参数是否为0，如果不是，将第二个参数添加到递归调用，并递减第一个参数。

上述定义 mult 宏的问题为，它调用了自身，所以没有方法将 mult 展开为一个纯 lambda表达式。因此，缩写是违法的。

4.6.1 自应用递归

乘法器函数如何获得自己的句柄？在 mult 宏被定义时，乘数函数的定义暂时不可用，而该定义在稍后才可用。特别的，当我们调用乘数函数得时候，我们必须有一个乘数函数的句柄。

因此，与直接引用自身不同，乘数函数可以让我们提供一个多重函数 t （它自身） 以及用于乘法的参数。更加精确地说，采用这种策略，我们定义的宏将不再是一个乘数函数，而是一个乘法器的制造者：它接收一些函数 t 并产生一个乘数函数，此函数将会期待两个参数并将它们相乘：

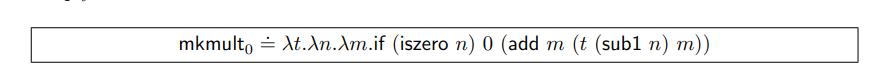
这个 mkmult₀ 宏即被定义完整了。并且（mkmult₀ t）产出一个乘数函数… 当 t 是乘数函数的时候！很明显，我们到目前为止仍然没有一个乘数函数。我们尝试将原来的 mult 定义本身参数化，但这样做之后就会失去 mult 的定义。

尽管我们无法提供 t 作为乘数函数，我们可以提供 t 作为乘数函数制造者。这想法会奏效，还是会造成无限的循环倒退？事实是，作为制造者确实能奏效。

假设将制造者应用于制造者就可以产生一个乘法器。则，应用于制造者的初始的参数 t 为制造者。 制造者的 body 部分，不管何处需要一个乘法器，我们使用 (t t) —— 因为 t 将会是一个制造者，并且应用一个制造者于自身将会生产出一个乘法器。下述是一个制造者 mkmult₁ ，其期待一个制造者的参数：

如果 mkmulti₁ 奏效，我们可以通过应用其自身得到乘数函数：

扫描二维码关注公众号，回复： 12744251 查看本文章

我们尝试将这个函数应用在 0 和 m（随机的m）上并看返回的是不是 0 。我们将只在必要的时候展开宏，并且我们假设 iszero 和 0 将会正确实现。

目前为止，一切都正常。如果我们将非零的 n 乘以 m，会得到什么？

由于 mult = (mkmult₁ mkmult₁)，上述过程的最后一步也可以被写作 (add m (mult (sub1 n) m))

因此，

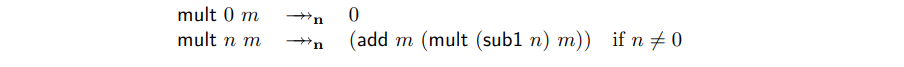
这正是我们需要的 mult add sub1 0 之间的关系。

练习4.11

定义一个 mksum 宏，使得 （mksum mksum) 表现得和一个求和函数一致，它将消费一个数字 n 并且将 0 到 n 的所有自然数相加返回。

题解

mksum ≐ λt.λn if (iszero n) 0 (add ((t t) (sub1 n)) n)

4.6.2 从自我应用弹出

上小节的方法能够让我们定义任何我们想要的递归函数。不过，这有点笨拙，因为我们必须定义一个制造函数，该函数会递归应用一个初始参数于自身。为了简便，我们需要将自应用的模式拉入其自身的抽象定义中。

更具体地说，我们需要一个函数，称其为 mk，它可以接收任何像 mkmult₀ 这样的制造者，并且生产出函数。举例来说，(mk mkmult₀) 会生产一个乘法器。

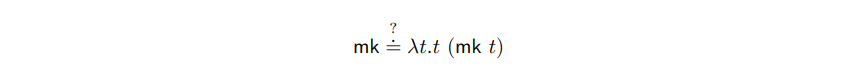
上述 mk 的定义是有缺陷的，但是我们可以由此糟糕的定义出发。mk 函数需要接收一个制造者 t 并且生产一个操作函数。即调用 (mk t) 则制造一个操作函数。

我们可以借助上一小节的方法来修复循环定义的 mk ：

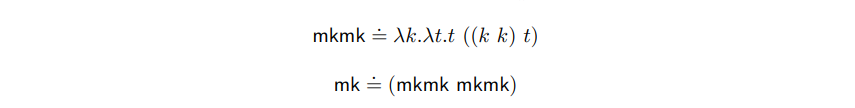
接下来让我们来验证 (mk mkmult₀) 的行为是否与 mult 一致：

4.6.3 定点与Y组合子

mk 函数现在看上去或许有点神秘。不知怎么的，它使 mkmult₀ 有用了，尽管 mkmult₀ 的设定是只有将乘法器传递给它之后它才能产出乘法器！

一般来说， mkmult₀ 可能接收任何函数，并且得到的“乘法器”将会由各种不同的行为，输出的函数通常也会与输入的函数有很大的不同。但是 mk 设法为 mkmult₀ 选择了一个输入函数，这样输出函数与输入函数保持相同。换句话说，mk 会找到 mkmult₀ 的定点。

事实证明，mk 可以找到任何函数的定点，换句话说，如果将 mk 应用于 M 产生 N，那么应用 M 于 N 将会再次产生相同的 N。

定理 4.1 对于任何 M， M (mk M) =_n (mk M)

定理 4.1的证明： 由于 =_n 是 →→_n 的对称闭合，我们可以通过证明 M →→_n M (mk M) 间接证明该定理：

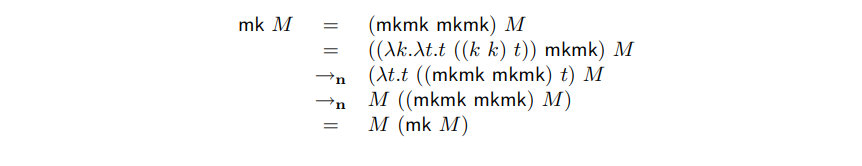
一个类似 mk 的行为的函数被称为 定点算子 。mk 函数只是它们中的一员。更加著名的定点算子被称为 Y：

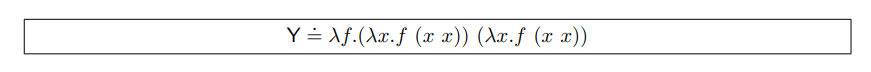
一般来说 Y 让我们更方便地定义递归函数。例如，我们可以这样定义 sum：

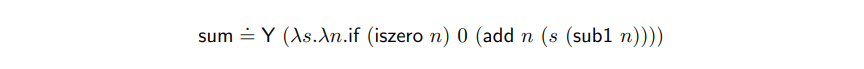
由于我们没有必要重复一个制造者表达式，我们可以略过 中间制造者 mksum，而直接应用 Y 于制造者函数。

此外，看到上述 sum 定义地程序员，会立即注意到 Y，看到 s 是Y的参数的参数，然后发现 λn… 作为递归函数 s 的定义。

练习 4.12

证明对于任何 M， M (Y M) =n (Y M)

题解

(Y M)
= ((λf.(λx.f (x x)) (λx.f (x x))) M)
→nβ (λx.M (x x)) (λx.M (x x))
→nβ (M ((λx.M (x x)) (λx.M (x x))))

M (Y M)
= M ((λf.(λx.f (x x)) (λx.f (x x))) M)
→nβ (M ((λx.M (x x)) (λx.M (x x))))

左边=右边，因此成立。

练习 4.13

定义 Lisp 地址对的编码，它由以下宏组成：

• null，一个常量
• cons，两个参数，返回一个地址对
• car，如果参数为 null ，返回 true；如果参数为 地址对 ，返回 false
• cdr，接收地址对为参数并且返回地址对的第二个元素。

你的编码必须满足以下等式：

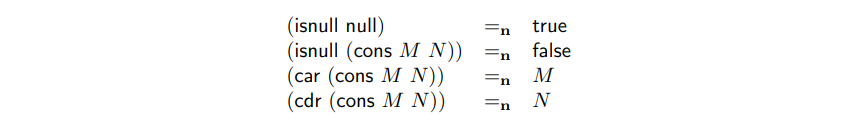
你的编码不需要为表达式指定任何特定的含义，如 (car null) 或是 (car cons)

题解

• null ≐ ⟨true, false⟩
• cons ≐ λM.λN ⟨false, ⟨M, N⟩⟩
• isnull ≐ λM.fst M
• car ≐ λM.fst (snd M)
• cdr ≐ λM.snd (snd M)

练习 4.14

使用你上个练习完成的编码，定义 length，它接收一个布尔值的列表，返回列表中的地址对。布尔值列表要么是 null，要么是 (cons b l)，其中 b 为 布尔值， l 是布尔值的列表。

题解

length ≐ Y (λf.λM.if (isnull M) 0 (add1 (f (cdr M))))